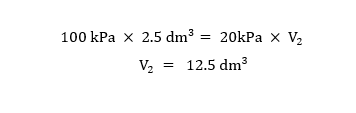නියත වූ උෂ්ණත්වයක් යටතේ ඇති ස්ථිර වායු ප්රමාණයක/ ස්කන්ධයක පීඩනය වායු පරිමාවට ප්රතිලෝමව සමානුපාතික වේ. එනම් පහත් පරිදි වේ
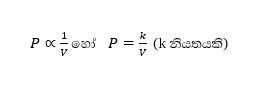
බොයිල් නියමය ව්යුත්පන්න කිරීම සඳහා පරිපූර්ණ වායු නියමය යොදා ගත හැකිය
වායුවේ ප්රමාණය හා පද්ධතිය උෂ්ණත්වය නියතව පවත්වා ගන්නේ නම් nT ගුණිතය නියතයක් වේ. R ද නියතයක් වන බැවින් nRT ගුණිතයද නියතයක්(k) වේ.
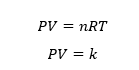
නියත උෂ්ණත්වයේ දී නියත වායු ප්රමාණයක පීඩනයේත් පරිමාවේත් ගුණිතය නියතයක් වේ. මෙය බොයිල් නියමය ප්රකාශ කරන තවත් ආකාරයකි.
නියත T උෂ්ණත්වයක ඇති නියත වායු පරිමාවV1 ද පීඩනය P1 ද නම් එය V2 පරිමාවට හා P2 පීඩනයට පත් කළ විට බොයිල් නියමයට
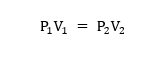
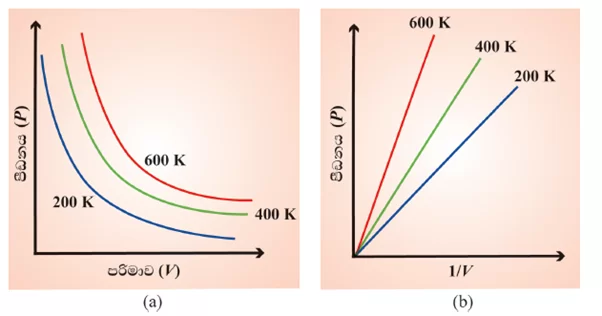
(a) රූපය මගින් සංසන්දනය සඳහා විවිධ උෂ්ණත්වවලදී PV=k ප්රස්තාර ගත කර ඇත. k අගය උෂ්ණත්වය මත රඳා පවතින නිසා දෙන ලද වායු ස්කන්ධය සඳහා අඳින ලද සෑම චක්රයක් සඳහාම k එකිනෙකට වෙනස් වේ. ඉහල උෂ්ණත්ව වලදී පරිමාවේ ප්රසාරණය නිසා චක්රය ඉහලට එසවේ.
(b) රූපය මගින් ද P ඉදිරියෙන් 1/V හි ප්රස්ථාරය නිරූපණය වේ. මීට අනුවට අනුව වායු ස්කන්ධයක් සම්පිණ්ඩනය කළ විට එකම ප්රමාණයකින් ඇති අණු සංඛ්යාව ඉතා කුඩා පරිමාවක් තුළ පැතිරේ.මේ අනුව ඉහළ පීඩන වලදී වායුවේ ඝනත්වය වැඩි වේ.
දෙන ලද වායුවක ඝනත්වය d,ස්කන්ධය m ද, පරිමාව v ද වන විට d=m/d සමීකරණයෙන් ලබාදේ. එම නිසා නියත වූ උෂ්ණත්වයේ දී,
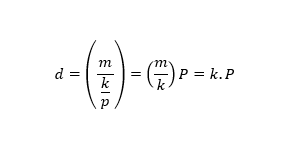
1.2 නිදසුන
නියත උෂ්ණත්වයක් යටතේ ඇති දන්නා වායු මවුල ප්රමාණයක පරිමාව දෙගුණ කළ විට පීඩනයේ සිදුවන වෙනස් වීම ගණනය කරන්න.
විසඳුම :
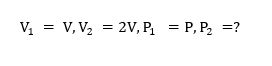
බොයිල් නියමය යෙදීමෙන් : P1V1=P2V2
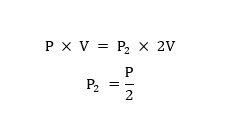
1.3 නිදසුන
කාමර උෂ්ණත්වයේ දී බැලුනයක් හයිඩ්රජන් වායුව දන්නා ප්රමාණයකින් පුරවා ඇත. වායුගෝලීය පීඩනයේ දී එම වායු ප්රමාණය 2.50 ක පරිමාවක් ගනී. එම උෂ්ණත්වයේ දී ම ඇතුළත පීඩනය 20 kPa වීමට බැලුනයේ පරිමාව කොපමණ විය කළ යුතු ද?
විසඳුම :
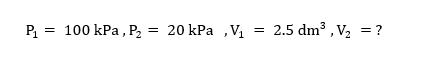
බොයිල් නියමය යෙදීමෙන් : P1V1=P2V2