හැඳින්වීම
- රළු පෘෂ්ඨයක් මත තබා ඇති වස්තුවක් පෘෂ්ඨයට සාපේක්ෂව චලිත වීමට උත්සාහ කිරීමේදී මෙන්ම පෘෂ්ඨයට සාපේක්ෂව චලිත වීමේදී, පෘෂ්ඨය මගින් වස්තුව මත ඇතිවන ප්රතිරෝධී බලය අපි ඝර්ෂණ බලය ලෙස හඳුන්වනු ලැබේ.
- එසේම ද්රව හෝ වායු මාධ්යයන් තුළින් වස්තුවක් චලනය කිරීමේදී එම මාධ්යය මගින් වස්තුව මත චලිතයට විරුද්ධව ප්රතිරෝධී බලයක් යෙදේ. මෙම ප්රතිරෝධී බලය දුස්ස්රාවී ඝර්ෂණ බලය ලෙස හැඳින්වේ.
- උදා:- පිහිනුම්කරුවෙකු ජලාශයක් හරහා පිහිනීමේදී ඔහු මත ජලය මගින් ඇති කරන ප්රතිරෝධී බලය දැනේ.
- ද්රව සහ වායු තුළ ඝර්ෂණ බලවලට හේතුවන ගුණාංගය දුස්ස්රාවිතාව ලෙස හැඳින්වේ.
- ද්රවයක උකු බව රඳා පවතින්නේ එම ද්රවයේ දුස්ස්රාවිතාව මතයි.
- ද්රවයක දුස්ස්රාවිතාව ව වැඩි වන විට එමගින් ඇති කරන ඝර්ෂණ බල විශාල වේ. එමනිසා උකු බව වැඩිවේ. සාපේක්ෂව සෙමෙන් ගලා යයි.
- ද්රවයක දුස්ස්රාවිතාව අඩු වන විට එමගින් ඇති කරන ඝර්ෂණ බල කුඩා වේ. එමනිසා උකු බව අඩු වේ. සාපේක්ෂව වේගයෙන් ගලා යයි.
- අඩු දුස්ස්රාවිතාවක් ඇති ජලයට වඩා වැඩි දුස්ස්රාවිතාවක් ඇති පොල්තෙල්වල උකු බව වැඩි වේ. එමනිසා පොල්තෙල් ජලයට වඩා සෙමෙන් ගලා යයි.
තරල ප්රවාහ
- තරලයක් ගලා යාමේදී සිදු වන්නේ එය මත ක්රියා කරන ගුරුත්වාකර්ෂණය හෝ වෙනයම් බාහිර බලපෑමක් යටතේ ද්රව්ය විරූපණ ප්රත්යාබලයකට ලක්වීමයි.
- සාමාන්යයෙන් ඝන ද්රව්යයක් විරූපණ ප්රත්යාබලයකට ලක් වූ විට එය නිශ්චිත විරූපණ වික්රියාවක් ඇතිකර ගනී.
- එහෙත් ද්රවයක් කිසියම් විරූපණ ප්රත්යාබලයකට ලක්වූ විට එහි ඇතිවන විරූපණ වික්රියාව කාලය සමඟ නිරතුරුව වෙනස් වේ. ඒ අනුව ද්රවය ප්රවාහ වේ.
- ද්රවයක දුස්ස්රාවිතාව වැඩිවත්ම එහි විරූපණ වික්රියාව කාලය සමඟ වෙනස් වන සීඝ්රතාවය හෙවත් ද්රවය ප්රවාහ වන සීඝ්රතාවය අඩුවේ.
- ඒ අනුව දුස්ස්රාවිතාව තරලයක් ප්රවාහ වීම කෙරෙහි බලපාන ප්රතිරෝධය පෙන්නුම් කරන ගුණාංගයකි.
අනවරත ප්රවාහය හෙවත් නොසැලෙන ප්රවාහය
- තරල ප්රවාහය ක කිසියම් ලක්ෂ්යයකදී අංශූන්ගේ ප්රවේගයේ විශාලත්වය හා දිශාව කාලය සමඟ වෙනස් නොවේ නම් එය අනවරත ප්රවාහයක් ලෙස හඳුන්වනු ලැබේ.
- තරල ප්රවාහයක් ප්රධාන වශයෙන් ආකාර 2කි.
- අනාකූල ප්රවාහය / ආස්තරීය ප්රවාහය
- ආකූල ප්රවාහය
අනාකූල ප්රවාහය හෙවත් ආස්තරීය ප්රවාහය
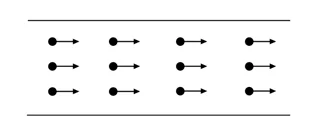
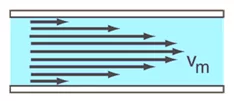
- යම් තරලයක් ස්තර වශයෙන් ප්රවාහ වන්නේ නම්, එය අනාකූල ප්රවාහයක් හෙවත් ආස්තරීය ප්රවාහයකි.
- මෙය විශේෂ ආකාරයේ අනවරත ප්රවාහයකි.
- තිරස්ව ගලායන අනාකූල ප්රවාහයක ඕනෑම අනාකූල රේඛාවක පවතින ද්රව අංශු සියල්ලම එකම වේගයෙන් චලනය වේ.
- එහෙත් එක් එක් අනාකූල රේඛාවේ පවතින ද්රව අංශුවල වේග එකිනෙකට වෙනස් විය හැක.
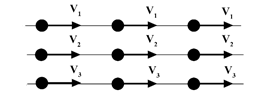
- ආස්තරීය ප්රවාහයක නිදහස් පෘෂ්ඨය සිට පහළට යාමේදී ද්රව ස්ථරවල වේගය අඩුවේ. ඝන පෘෂ්ඨයක් සමග ස්පර්ශ වී ඇති පහළම ද්රව ස්ථරය චලනය නොවේ. එහි ප්රවේගය ශුන්ය වේ.
ආකූල ප්රවාහය
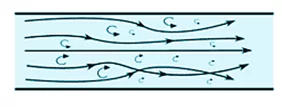
- ද්රව අංශු කැළඹෙමින් ප්රවාහය වන විට එය ආකූල ප්රවාහයක් ලෙස හඳුන්වනු ලැබේ.
- මෙවැනි ද්රව ප්රවාහයක කිසියම් ස්ථානයක පවතින ද්රව අංශුවල ප්රවේග කාලය සමග විශාලත්වයෙන් සහ දිශාවෙන් නිරතුරුවම වෙනස් වේ.
- ද්රවයක් ගලායන තිරස් නලයක දෙකෙළවර අඩු පීඩන අන්තරයක් පවතින විට නලය තුළින් ද්රවය ගලනුයේ අනාකූල ප්රවාහයක් ලෙස හැසිරෙමිනි.
- දෙකෙළවර පවතින පීඩනය අන්තරය වැඩිකරන විට ද්රව අංශු ගලායන වේග වැඩිවන අතර ද්රව අංශුවල වේගය අවධි වේගය ඉක්මවූ විට ආකූල ප්රවාහයක් ලෙස හැසිරේ.
- අවධි වේගය යනු අනාකූල ලක්ෂණ පෙන්නුම් කරමින් ද්රව අංශුවලට ප්රවාහ විය හැකි උපරිම වේගයයි. එය ඉක්මවූ පසු ද්රවය කැළඹීම් සහිත ආකූල ප්රවාහයක් ලෙස හැසිරේ.
ද්රව ප්රවාහයක් සඳහා ස්පර්ශීය ප්රත්යාබලය සහ ප්රවේග අනුක්රමණය
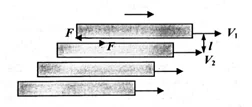
- ආස්තරීය ප්රවාහයක හැසිරෙමින් ගලා යන ද්රවයක ස්ථරීය ප්රවාහයක් දැකිය හැක.
- ද්රවයට දුස්ස්රාවී ගුණය ලැබෙනුයේ එකිනෙකට සාපේක්ෂ ලෙස චලිත වන අනුයාත ද්රව ස්ථර අතර යෙදෙන ඝර්ෂණ බලය හේතුවෙනි.
- මෙම ඝර්ෂණ බලය ද්රව ස්ථරවලට ස්පර්ශීය ලෙස ක්රියා කරයි.
- රූපයේ පරිදි අනුයාත ද්රව ස්ථර දෙකෙන් ඉහළින් පවතින ස්ථරය (නිදහස් පෘෂ්ඨයට වඩාත් ආසන්න ස්ථරය) ඊට පහළින් පවතින ද්රව ස්ථරය මත සර්පණය වන විට පහළින් පවතින ද්රව ස්ථරය මත F ස්පර්ශී ඝර්ෂණ බලයක් යොදවනු ලබයි. ඒ සමඟම ඉහල ස්ථරය මගින් පහළ ස්ථරය මතද F ස්පර්ශී ඝර්ෂණ බලයක් යොදවනු ලබයි. එම බලය හේතුකොටගෙන පහළ ද්රව ස්ථරය ඉහළ ස්ථරය චලිත වන දිශාවට චලනය වේ.
- මේ හේතුවෙන් ද්රව ස්ථර සියල්ල එකම දිශාවට චලිත වන අතර නිදහස් පෘෂ්ඨයේ සිට පහළට යාමේදී ඒවායේ චලිත වේග අඩුවේ.
- කිසියම් ද්රව ස්ථරයක ඒකක වර්ගඵලයක් මත ක්රියා කරන ස්පර්ශී ඝර්ෂණ බලය ස්පර්ශී ප්රත්යාබලය ලෙස හැඳින්වේ.
- ද්රව ස්ථරයේ A වර්ගඵලයක් මත ක්රියා කරන ස්පර්ශී ඝර්ෂණ බලය F නම්,

- රූපයේ පරිදි ඉහළින් පවතින ද්රව ස්ථර දෙකෙහි චලිත වේග V1 හා V2 (V1>V2) ද ඒවා අතර පරතරය d ද විට එම ස්ථරය සඳහා,

නිව්ටන් සමීකරණය
- ආස්තරීය ප්රවාහයක හැසිරෙමින් ගලායන ද්රවයක අනුයාත ස්ථර දෙකක් අතර පවතින ස්පර්ශී ඝර්ෂණ බලය හේතුවෙන් ඇතිවන ස්පර්ශීය ප්රත්යාබලය එම ස්තර අතර වූ ප්රවේග අනුක්රමණයට අනුලෝම ලෙස සමානුපාතික වේ.

η යනු දුස්ස්රාවිතා සංගුණකයයි
දුස්ස්රාවිතා සංගුණකයේ අර්ථ දැක්වීම
- ආස්තරීය ප්රවාහයක හැසිරෙමින් ගලා යන ද්රවයක ඒකක ප්රවේග අනුක්රමණයක් යටතේ ඊට අභිලම්භ ලෙස චලනය වන ද්රව ස්ථරයක ඒකක වර්ගඵලයක් මත ස්පර්ශීය ලෙස ක්රියා කරන දුස්ස්රාවී ඝර්ෂණ බලය හෙවත් ස්පර්ශීය ප්රත්යාබලය එම ද්රවයේ දුස්ස්රාවිතා සංගුණකය වේ.
- දුස්ස්රාවිතා සංගුණකයේ ඒකක – kg m-1 s-2 N s m-2
- දුස්ස්රාවිතා සංගුණකයේ මාන – ML-1T-1
Q: තිරස් සමතල පෘෂ්ඨයක් මත 2mm ඝනකමට දුස්ස්රාවිතා සංගුණකය 1.2 N s m-2 වන තෙල් පටලයක් අතුරා ඒ මත වර්ගඵලය 0.1m2 වන තහඩුවක් තබා ඇත. තහඩුව 0.1 cm s-1 වේගයකින් චලනය කරවීම සඳහා තහඩුවට ස්පර්ශ ලෙස යෙදිය යුතු බලයේ විශාලත්වය සොයන්න. තෙල් පටලය ආස්තරීය ප්රවාහයක් ලෙස හැසිරෙන්නේ යැයි සලකන්න.
විසඳුම:-
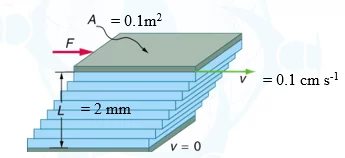
තෙල් පටලයේ තහඩුව සමඟ ස්පර්ශිත ස්ථරය තහඩුව චලනය වන වේගයෙන් චලනය වන ලෙසද, තෙල් පටලයේ සමතල පෘෂ්ඨය සමඟ ස්පර්ශිත ස්ථරය නිශ්චලව පවතින්නේ යැයිද සැලකිය හැක.
නිව්ටන් සමීකරණයට අනුව,
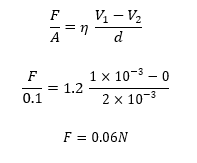
පොයිසෙල් සමීකරණය
- නළයක් තුළින් ද්රවයක් ගලනුයේ නළය දෙකෙළවර පීඩන අන්තරය හේතුවෙනි.
- පීඩන අන්තරය කුඩා වන විට ද්රවය සෙමින් ගලන අතර පීඩන අන්තරය වැඩිවීමත් සමග ද්රව්ය ගලන වේගයද වැඩි වේ.
- අරය a හා දිග l වන තිරස් කේශික නලයක් තුළින් දුස්ස්රාවිතාව η වන ද්රවයක් අනාකූල ලෙස ගලා යන්නේ යැයි සිතමු.
- එම නළය තුළින් ඒකීය කාලයකදී ගලා ගිය මුළු ද්රව පරිමාව සඳහා පොයිසෙල් විසින් පහත සූත්රය යොදාගෙන ඇත.
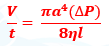
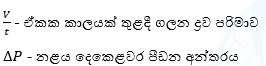
- ඉහත සමීකරණය සත්ය වීමට පහත අවශ්යතා තෘප්ත කළ යුතුය.
- නළය කේශික නලයක් විය යුතුය.
- නළය තිරස් විය යුතුය.
- නළය තුල ද්රවය අනවරත, අනාකූල චලිතයක් සිදුකල යුතුය.
- නළය ඍජු විය යුතුය.
- ද්රවය අසම්පීඩ්ය විය යුතුය.
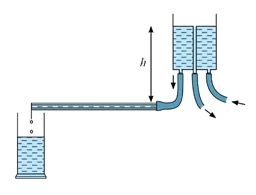
Q: බඳුනක පතුලට ආසන්නව දිග 10cm සහ අභ්යාන්තර විෂ්කම්භය 2mm වන තිරස් නළයක් සම්බන්ධ කර බඳුන ජල කරාමයක පහළින් තබා ඇත. කරාමයෙන් නියත සීඝ්රතාවයෙන් යුතුව ජලය ගලා යන පරිදි විවෘත කළ විට බඳුන තුළ ජල මට්ටම 10cm දක්වා ඉහළ නැග සමතුලිත විය. කරාමයෙන් ජලය පිටවන සීඝ්රතාව ගණනය කරන්න. ජලයේ දුස්ස්රාවිතා සංගුණකය = 1.0 × 10-3 Nsm-2, ජලයේ ඝනත්වය 1000 kgm-3.
විසඳුම:-
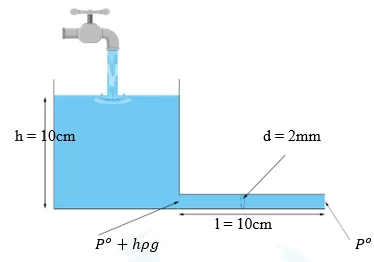
නලය තුළින් ගලන ජල ප්රවාහය අනාකූල සහ අනවරත යැයි පළමුවෙන් උපකල්පනය කළ යුතුය.
බඳුනේ ජල මට්ටම ඉහළ යන විට නලයේ එම කෙළවරේ පීඩනයද ක්රමයෙන් වැඩි වේ. අනෙක් කෙළවරේ ඇත්තේ වායුගෝලීය පීඩනයයි.
බඳුනේ ජල මට්ටම ඉහළ යාම නැවතුණු පසු නළය දෙකෙළවර පීඩන අන්තරය නියත වන අතර, කරාමයෙන් ජලය පිටවන සීඝ්රතාවය, නළය තුළින් ජලය ගලා යන සීඝ්රතාවයට සමාන වේ. එවිට අනවරත තත්ත්වයක් ගොඩනැගේ.
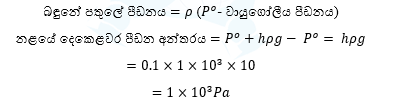
පොයිසෙල් සමීකරණය යෙදීමෙන්,

ඒ අනුව කරාමයෙන් ජලය පිටවන සීඝ්රතාවයද 3.93 × 10-6 m3s-1
ස්ටොක්ස් නියමය
- දුස්ස්රාවී මාධ්යයක් තුළින් ගෝලාකාර වස්තුවක් ගමන් කිරීමේදී එම වස්තුව හා ස්පර්ශ වී ඇති දුස්ස්රාවී මාධ්යය මගින් මෙම වස්තුවේ චලිතය වැළැක්වීමට චලිත දිශාවට ප්රතිවිරුද්ධ දිශාවට වස්තුව මත දුස්ස්රාවී ඝර්ෂණ බලයක් ඇති කරයි.
- අරය a වන ගෝලාකාර වස්තුවක් v ප්රවේගයෙන් දුස්ස්රාවිතාව වන මාධ්යයක් තුළින් ගමන් කරන්නේ යැයි සිතමු.
- එවිට වස්තුව මත ක්රියා කරන දුස්ස්රාවී බලය F නම්,
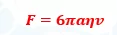
- මෙය ස්ටොක්ස් සමීකරණය වේ.
- ඉහත ගෝලය ඝන වුවත් කුහර වුවත් දුස්ස්රාවී බලය සඳහා සමීකරණය සත්ය වේ.
- එසේම ගෝලයන් ඒකාකාර ප්රවේගයෙන්යෙන් ත්වරණයෙන් හෝ මන්දනයෙන් ගමන් ගත්තද මෙම නියමය සත්ය වේ.
- නිශ්චල ජලාශයක මධ්යයට 10cm අරයක් ඇති බෝලයක් 20 ms-1 ප්රවේගයෙන් විසි කරනු ලැබේ. බෝලය ප්රථමයෙන් සම්පූර්ණයෙන් ගිලෙන මොහොතේදී එය මත ක්රියා කරන දුස්ස්රාවී බලය කොපමණද? (ජලයේ දුස්ස්රාවීතා සංගුණකය 9×10-4 Pa s වේ.)
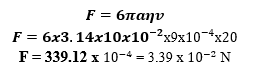
- එම බෝලය මතම 5×10-2 N දුස්ස්රාවී බලයක් ඇති වීමට එය එම ප්රවෙගයෙන්ම විසි කල යුතු ද්රවයේ දුස්ස්රාවීතා සංගුණකය කොපමණද?
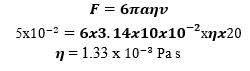
- ස්ටොක්ස් සමීකරණය වලංගු වන තත්ත්ව:
- මාධ්යය නිශ්චලව පැවතිය යුතුය.
- ගෝලයේ ප්රමාණය හා සැසදීමේදී මාධ්යය ඉතා විශාල ප්රදේශයක් පුරා පැවතිය යුතුය.
- වස්තුව අවට මාධ්ය ස්ථර අනාකූල තත්ත්වයේ පැවතිය යුතුය.
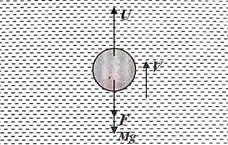
දුස්ස්රාවී මාධ්යයක් තුළින් වැටෙන ගෝලාකාර වස්තුවක ආන්ත ප්රවේගය සඳහා ප්රකාශනයක් ලබාගැනීම.
- අරය a හා ඝනත්වය ρ වන ඝන ගෝලයක් ඝනත්වය σ වන දුස්ස්රාවිතා සංගුණකය η වන මාධ්යයක් තුළින් නිශ්චලතාවයෙන් යුතුව මුදාහරින්නේ යැයි සිතමු.
- ආරම්භයේ දී ගෝලය නිශ්චල බැවින් දුස්ස්රාවිතා ඝර්ෂණ බලය ශූන්ය වේ.
- ගෝලයේ බර උඩුකුරු තෙරපුමට වඩා විශාල නම් බෝලයට අසංතුලිත බලයක් ලැබේ.
- එවිට ගෝලය පහළට ත්වරණයෙන් ගමන් කිරීම ආරම්භ කරයි.
- ස්ටොක්ස් සමීකරණයට අනුව ගෝලය මත දුස්ස්රාවී බලයක් ක්රියාත්මක වේ.
- එය සෑම විටම ගෝලයේ චලිත දිශාවට ප්රතිවිරුද්ධ වේ.
- යම් අවස්ථාවක ගෝලයේ ප්රවේගය v නම් දුස්ස්රාවී ඝර්ෂණ බලය 6πaηv වේ.
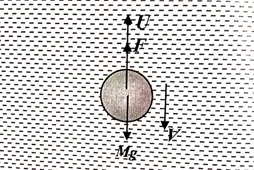
- මෙම දුස්ස්රාවී ඝර්ෂණ බලය ගෝලයේ ප්රවේගය වැඩිවත්ම වැඩිවේ.
- එවිට යම් අවස්ථාවක u+F වල අගය mg අගයට සමාන වේ.
- එවිට ගෝලය මත අසංතුලිත බලයක් ක්රියා නොකරයි.
- ප්රවේගය තවදුරටත් වැඩි නොවන නිසා දුස්ස්රාවී ඝර්ෂණ බලය ද නියතව පවති.
- ගෝලය එම අවස්ථාවේදී ලබාගෙන ඇති ප්රවේගයෙන්ම චලිත වේ.
- මෙම ප්රවේගය ආන්ත ප්රවේගය ලෙස හඳුන්වයි.
- වස්තුවේ ආන්ත ප්රවේගය සඳහා ප්රකාශනයක් පහත දැක්වෙන ආකාරයට ලබාගගත හැක.
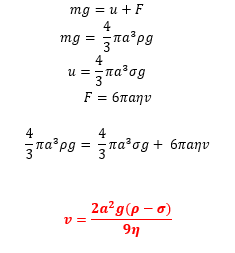
Q: ගෝලාකාර පළතුරක් ගසක සිට නිශ්චල ජලාශයකට ඇද වැටේ. එහි අරය 7.5cm ද එහි ඝනත්වය 1500kgm-3 ද වේ. ජලයේ ඝනත්වය 1000 kgm-3 ද දුස්ස්රාවීතා සංගුණකය 9×10-4 Pa s ද වේ නම් එම පලතුරේ ආන්ත ප්රවේගය සොයන්න.
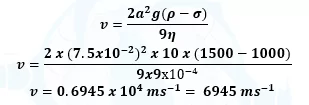
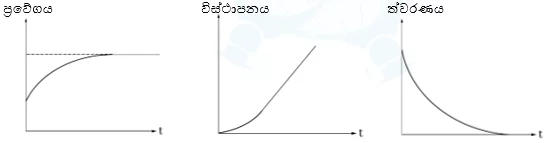
ගෝලයේ චලනය සඳහා ප්රවේග-කාල, විස්ථාපන-කාල හා ත්වරණ-කාල ප්රස්තාර පහත දැක්වේ.
- ඉහත ගෝලාකාර වස්තුව තනනු ලැබූ ද්රව්යයේ ඝනත්වය මාධ්යයේ ඝනත්වයට වඩා අඩු වන විට මාධ්යය තුළ වස්තුව ඉහලට ගමන් කරයි.
- එවැනි අවස්ථාවක වස්තුව මත ක්රියා කරන දුස්ස්රාවී ඝර්ෂණ බලයෙහි දිශාව සිරස් ලෙස පහළට වන අතර වස්තුවේ ආන්ත ප්රවේගය සඳහා ප්රකාශනයක් පහත් දැක්වෙන ආකාරයට ලබාගගත හැක.
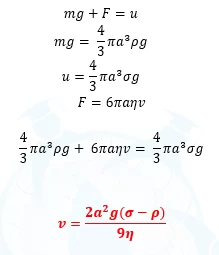
ප්රායෝගික පරීක්ෂණය- කේශික ප්රවාහ ක්රමය භාවිතයෙන් ජලයේ දුස්ස්රාවිතා සංගුණකය සෙවීම (පොයිසෙල් සමීකරණය ඇසුරෙන්)
අවශ්ය ද්රව්ය හා උපකරණ:-
- 25 cm පමණ දිග කේශික නලයක්
- නියත පීඩන උපකරණයක්
- මිනුම් සරාවක්
- මීටර් කෝදුවක්
- විරාම ඝටිකාවක්
- චල අන්වීක්ෂයක්
- නූල් කැබැල්ලක්
- තනුක භෂ්මයක් හා අම්ලයක්
- ස්ප්රීතු ලෙවලයක්
ක්රමය:-
- කේශික නලයක් පළමුවෙන් තනුක සෝඩියම් හයිඩ්රොක්සයිඩ් ද්රාවණයෙන් හා දෙවනුව තනුක හයිඩ්රොක්ලෝරික් අම්ල ද්රාවණයෙන් සෝදා අවසානයේ ජලයෙන් සෝදාගන්න.
- රූපයේ දැක්වෙන ආකාරයට උපකරණ සකස් කර කේශික නලය ස්ප්රීතු ලෙවලයක් මගින් තිරස්ව සවිකරගන්න.
- කේශික නලයේ විවෘත කෙළවර අසලින් නූල් කැබැල්ලක් ගැටගසා කරාමය ඇර කේශික නලයේ ජලය සෙමෙන් වෑස්සෙන අයුරින් නියත පීඩන උපකරණය සකස් කරන්න.
- විරාම ඝටිකාව ක්රියාත්මක කරනවාත් සමඟම නලයේ විවෘත කෙළවර යටින් මිනුම් සරාව තබන්න.
- මිනිත්තු තුනක් පමණ නිශ්චිත කාලයක් තුළ මිනුම්සරාව තුළ එකතු වූ ජල පරිමාව සටහන් කරගන්න.
- නියත පරිමා උපකරණයේ ජල මට්ටමත් කේශික නලයත් අතර සිරස් උස (h) මීටර් කෝදුවක් භාවිතයෙන් මැනගන්න.
- නියත පීඩන උපකරණයේ පිහිටීම් වෙනස් කරමින් h හි අගයන් කිහිපයක් සඳහා ඉහත සඳහන් ආකාරයට පාඨාංක ලබා ගන්න.
- කේශික නලයේ දිග මීටර් කෝදුවෙන්ද කේශික නලයේ අභ්යන්තර විෂ්කම්භය එකිනෙකට ලම්භක දිශා දෙකක් ඔස්සේ චල අන්වීක්ෂයකින්ද මැන ගන්න.
පරීක්ෂණයේ වැදගත් කරුණු:-
- පොයිසෙල් සමීකරණය වලංගු වීම සඳහා ජල ප්රවාහය අනාකූල සහ අනවරත විය යුතුය. නියත පීඩන උපකරණය මගින් කේශික නලය දෙපස නියත පීඩන අන්තරයක් තබාගෙන අනාකූල සහ අනවරත ප්රවාහයක් ලබාදේ
- කේශික නලයේ කෙළවරෙහි කපු නූල් කැබැල්ලක් යොදා ඇත්තේ නළය දිගේ ජලය ඉවතට ගැලීම වළක්වාලීමටත් ජල පෘෂ්ඨය පෘෂ්ඨික ආතතිය නිසා පීඩන වෙනසක් ඇතිවීම වළක්වා ලීමට ය.
- h අගය පහළ අගයක තබාගත යුතුය. එමගින් නලයේ දෙකෙළවර පීඩන අන්තරය පහළ අගයක් තබා ගත හැක. එම්ගින් සෑම විටම අනාකූල ප්රවාහය පවත්වා ගත හැක.
- ප්රකාශනයේ a4 පදයක් අඩංගුවන නිසා මෙම පරීක්ෂණයේදී වඩාත් නිවැරදිව නලයේ විෂ්කම්භය මැන ගැනීම වැදගත් වේ.
පරික්ෂණයේදී සිදුවන ගණනය:-
නළයේ දෙකෙළවර පීඩන අන්තරය = P0 + h𝜌g – P0 = h𝜌g
පොයිසෙල් සමීකරණය යෙදීමෙන්,
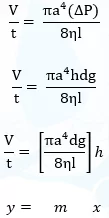
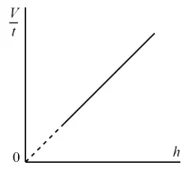
ප්රස්තාරයේ අනුක්රමණය (m) සොයා ගැනීමෙන් පසු ජලයේ දුස්ස්රාවිතා සංගුණකය (η) පහත පරිදි ගණනය කළ හැක.
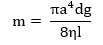
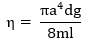
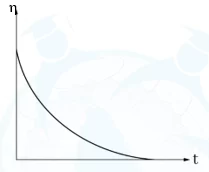
ද්රවවල දුස්ස්රාවිතාව උෂ්ණත්වය අනුව වෙනස් වීම
- උෂ්ණත්වය වැඩි වීමත් සමඟ ද්රවවල උකු බව අඩුවී ගලා යාමේ හැකියාව වැඩිවේ. එනම් උෂ්ණත්වය වැඩි කළ විට ද්රවවල දුස්ස්රාවිතාව අඩුවේ. ද්රවවල දුස්ස්රාවිතාව උෂ්ණත්වය සමඟ විචලනය වන ආකාරය පහත ප්රස්තාරයෙන් දැක්විය හැක.