රේඛීය ගම්යතාව
රේඛීයව චලනය වන වස්තුවක් සඳහා රේඛීය ගම්යතාව පහත ලෙස ගනී.
රේඛීය ගම්යතාව = ස්කන්ධය x ප්රවේගය
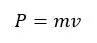
මාන සළකා,
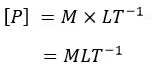
ගම්යතාවයේ ඒකකය, kg m s-1
ව්යුත්පන්න ඒකකය, Ns
රේඛීය ගම්යතා සංස්ථිති නියමය
1. පද්ධතියක් මත සලකනු ලබන යම් දිශාවක් ඔස්සේ “සම්ප්රයුක්ත ආවේගයක්” නොමැති නම් එම දිශාවට ගම්යතාව නියතව පවතියි.ඉතා කුඩා කාලයක් තුළ වස්තුවක් තුළ විශාල බලයක් ක්රියාත්මක වන විට “ආවේගයක්” ඇති බව කියනු ලැබේ.
2. නිව්ටන්ගේ දෙවන නියමයෙන්,
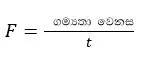
ගම්යතා වෙනස = Ft
F = 0 නම්, එනම් බලය ශුන්ය නම් ගම්යතා වෙනස ද ශුන්ය වේ.
එනම් වස්තුවක් හෝ වස්තු පද්ධතියක් මත බාහිර බලයක් ක්රියා නොකරන විටදී දෙන ලද දිශාවක් ඔස්සේ එම වස්තුවල මුළු රේඛීය ගම්යතාව සංස්ථිතික වේ. (වෙනස් නොවේ)
එනම් ඉහත 1 හා 2 කරුණු මඟින් සමාන අර්ථ දෙනු ලැබේ.
උදා :-
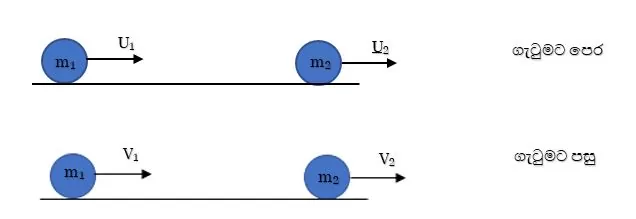
සුමට තිරස් තලයක් මත එකිනෙක සමඟ ගැටෙන සුමට ගෝල දෙකක් සළකන්න.
- සුමට තලයක් මත ගැටෙන බැවින් ඝර්ෂණ බල වැනි බාහිර බල නොමැත.එබැවින් රේඛීය ගම්යතා සංස්ථිති නියමය අනුව,
ගැටුමට පෙර ගම්යතාව = ගැටුමට පසු ගම්යතාව
m1u1 + m2u2 = m1v1 + m2v2
- මෙහිදී ඇත්තෙන්ම සිදුවන්නේ A මඟින් B මත ඇතිකරන බලයට සමාන ප්රතිවිරුද්ධ බලයක් B මඟින් A මත ඇති කිරීමයි.
- තවද එම බලයන් ක්රියා කරන කාලයන්ද සමානයි. එබැවින් A නිසා B මතද, B නිසා A මතද ඇතිකරන ආවේග (Ft) සමාන හා ප්රතිවිරුද්ධ වේ.
- එනම් ගම්යතා වෙනස = ආවේගය = F t
- එබැවින් ඇති වන ගම්යතා වෙනස් වීමද සමාන ප්රතිවිරුද්ධ වේ. එබැවින් ගම්යතා වෙනස ශුන්ය වේ.
සටහන-
m අදීශයක් වුවද u අදීශයක් නොවන බැවින් (එනම් ප්රවේගය දෛශිකයක් බැවින්) ගම්යතාවයද දෛශිකයකි.
එබැවින් රේඛීය ගම්යතා සංස්ථිති නියමය ද යෙදිය යුත්තේ කිසියම් නිශ්චිත දිශාවක් ඔස්සේය.




සැහැල්ලු තන්තුවකට 10g ස්කන්ධයක් ඈදා පද්ධතිය 4ms-2 ත්වරණයකින් පහලට වැටීමට සලස්වන ලදී.තන්තුවේ ආතතිය වන්නේ