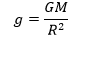05.01.00 – නිව්ටන්ගේ ගුරුත්වාකර්ෂණ නියමය

නිව්ටන්ගේ ගුරුත්වාකර්ෂණ නියමය

විශ්වයේ පවතින්නා වූ ඕනෑම වස්තූන් දෙකක් අතර ක්‍රියා කරන ගුරුත්වාකර්ෂණ බලය වස්තු වල ස්කන්ධ දෙකෙහි ගුණිතයට අනුලෝමවද ඒවා අතර පරතරයේ වර්ගයට ප්‍රතිලෝමවද සමානුපාතික වේ.

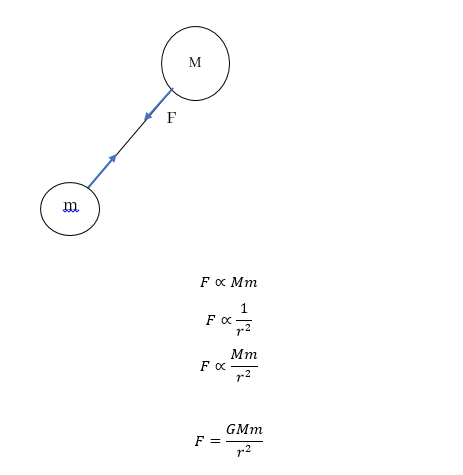
මෙහි G ගුරුත්වාකර්ශණ නියතයයි. එහි අගය G = 6.67×10^-11 Nm² kg^-2 වේ. G හි අගය ඉතා කුඩා බැවින් ගුරුත්වාකර්ෂණ බලය සදහා ප්‍රමාණවත් අගයක් ලැබෙන්නේ විශාල ස්කන්ධ සදහා පමණි.

G හි මාන,

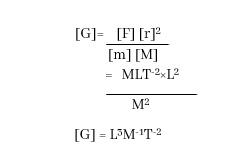
උදාහරණ:- 1) 1 km පරතරයකින් ඇති 10⁹kg සහ 10⁸ kg ස්කන්ධ දෙක අතර ගුරුත්වාකර්ෂණ බලය සොයන්න.

                 r =1×10³ m,    M =10⁹kg,   m = 10⁸kg

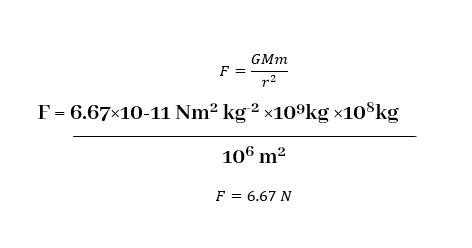
ගුරුත්වකර්ෂණ ක්ෂේත්‍ර තීව්‍රතාවය

යම් ප්‍රදේශයක ස්කන්ක්ධයක් තැබූ විට එය මත බලයක් ඇති වේ නම් එම ප්‍රදේශයේ ගුරුත්ව ක්ෂේත්‍රයක් ඇති බව අප දනිමු. යම් ලක්ෂයක තබන ලද ඒකක ස්කන්යධක් මත බලය එම ලක්ෂයේ ගුරුත්වජ ක්ෂේත්‍ර තීව්‍රතාව ලෙස හැදින්වේ. 

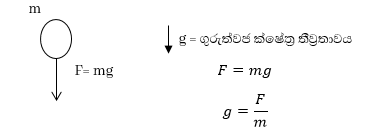
  g දෛශිකයකි. එහි ඒකක N kg^-1 වේ.

1. ලක්ෂීය ස්කන්ධයකට r දුරකින් පිහිටි ලක්ෂ්‍යය ක්ෂේත්‍ර තීව්‍රතාවය

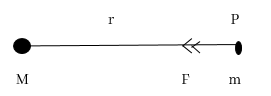
මෙහි දක්වා ඇති පරිදි  M  ස්කන්දයේ සිට r දුරකින් පිහිටි P ලක්ෂයේ ක්ෂේත්‍ර තීව්‍රතාවය සෙවීම සඳහා කල යුත්තේ P  නැමැති ලක්ෂ්‍යයේ ඉතා කුඩා m අවස්ථිතික ස්කන්ධයක් තබා එය මත හටගන්නා ගුරුත්වාකර්ෂණ බලය සෙවීමයි.එවිට එම බලය පහත පරිදි වේ,

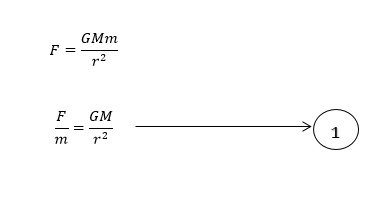
මෙම ලක්ෂ්‍යයේ ගුරුත්වාකර්ෂණ ක්ෂේත්‍ර තීව්‍රතාවය,

1 හා 2 න්,

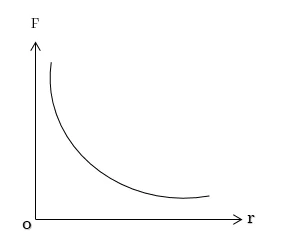
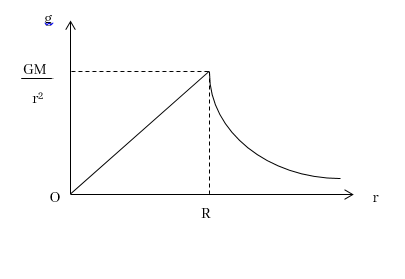
ලක්ෂ්‍යයාකාර ස්කන්ධයෙන් ඉවතට යනවිට එනම් r² වැඩිවන විට g  ප්‍රබලව අඩුවේ.

2. M ගෝලාකාර ස්කන්ධයක් නිසා  ඇතිවන ගුරුත්වජ ක්ෂේත්‍ර තීව්‍රතාවය,

                                                    

                                                                                                                     

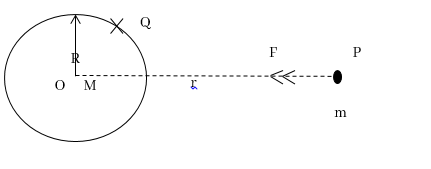
i. පිටතින් පිහිටි ලක්ෂ්‍යයක,

 P   හි තැබූ ස්කන්ධයක් මත බලය,

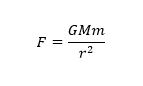
 අර්ථ දැක්වීමෙන් P  හි ගුරුත්වජ ක්ෂේත්‍ර තීව්‍රතාවය,

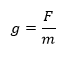
එමනිසා P  හි ගුරුත්වජ ක්ෂේත්‍ර තීව්‍රතාවය,

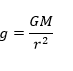
ii. පෘෂ්ඨය මත පිහිටි ලක්ෂ්‍යයක,(Q  වැනි)

          එවිට     R =r  වේ

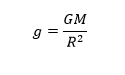
iii.       අභ්‍යන්තර ලක්ෂ්‍යයක,

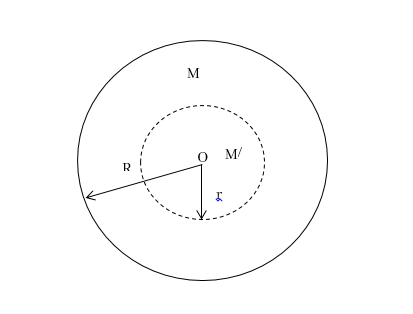
අරය  r වන ගෝලයේ ස්කන්ධය,   

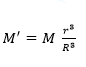
දැන් හි P  තැබූ  m ස්කන්ධය මත බලය,

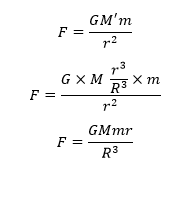
අමතර දැනුමට,

අරය  r වන ගෝලයේ ස්කන්ධය සෙවීම,

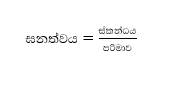
ස්කන්ධය M වන ගෝලය සලකා බලමු.

     

ස්කන්ධය M^/ වන ගෝලය සලකා බලමු.

        

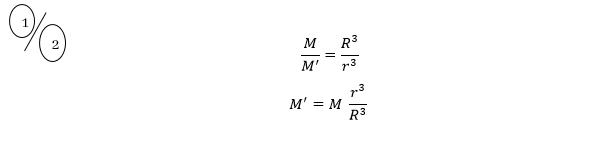
මෙහිදී r  ට පිටතින් ඇති බාහිර කවචය මගින් m මත ඇතිවන සම්ප්‍රයුක්ත බලය ශුන්‍ය වන බව අනුකලනය භාවිතයෙන් පෙන්විය හකිය.

එබැවින් P හි ගුරුත්වජ ක්ෂේත්‍ර තීව්‍රතාවය,

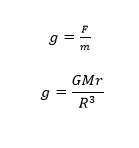
මෙහි අරය r  සමග ගුරුත්වජ ක්ෂේත්‍ර තීව්‍රතාවය g වෙනස්වන අයුරු පහත වේ.

3. පෘටිවි පෘෂ්ඨය අසල ගුරුත්වජ ක්ෂේත්‍ර තීව්‍රතාව

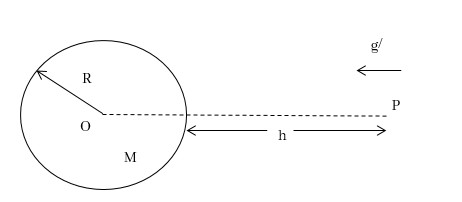
පෘට්වි කේන්ද්‍රයට (R + h)  දුරින් පිහිටි බාහිර ලක්ෂ්‍යයක ක්ෂේත්‍ර තීව්‍රතාවය,

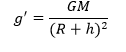
මෙහි (R + h) වැඩිවන විට ගුරුත්වජ ක්ෂේත්‍ර තීව්‍රතාවය අඩුය. එනම් පෘථිවි පෘෂ්ඨයෙන් ඈතට යනවිට ගුරුත්වජ ක්ෂේත්‍රය ක්‍රමයෙන් දුර්වල වේ.

පෘථිවි පෘෂ්ඨය මත ලක්ෂ්‍යයක ගුරුත්වජ ක්ෂේත්‍ර තීව්‍රතාවය,

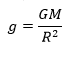
පොදු වශයෙන් ස්කන්ධය M සහ අරය R  වන ඕනෑම ඝන වස්තුවක් මත ගුරුත්වජ ක්ෂේත්‍ර තීව්‍රතාවය,