හැඳින්වීම
- තාර්කික ද්වාරයක් යනු බූලියන් ශ්රිතයක් ක්රියාවට නංවන්නාවූ එනම්, එකක් හෝ කිහිපයක් තාර්කික ප්රදානයන් මත තාර්කික මෙහෙයුමක් සිදුකොට එක් තාර්කික ප්රතිදානයක් ලබාදෙන්නාවූ පරාමාදර්ශිත හෝ භෞතික උපකරණයකි.
- එය ට්රාන්සිස්ටර භාවිතාකොට නිපදවා ඇති ඉලෙක්ට්රොනික උපාංගයකි.
- ද්වාර කපාට නමින්ද මෙය හඳුන්වයි. ඉලෙක්ට්රොනික භාවිතයේදී ලොජික් ගේට් යනුවෙන් හඳුන්වයි. ඉලෙක්ට්රොනික උපාංගවලට භාවිතා වන නම් සිංහලට පරිවර්තනයේදී සුළු අඩුපාඩුකම් ඇතිවීමට පුළුවන. කෙසේවෙතත් කාර්මිකයින් ගේට් යන තනි වචනයෙන් මෙය හඳුන්වයි.
- තාර්කිකව ක්රියා කරනු ලබන ඕනෑම ඉලෙක්ට්රොනික පරිපථයක එක ගේටයක් හෝ අන්තර්ගතයි.පරිගණකයද ඇතුළුව මේ සියලු තර්ක පරිපථ තර්ක මට්ටම් දෙකක් භාවිතා කරයි. එනම් බින්දුව සහ එක(0සහ1) වේ.
- විටක බින්දුව සෘණ තත්වය ලෙසද, එක ධණ තත්වය ලෙසද, විටක බින්දුව (OFF) තත්වය ලෙසද, එක (ON)තත්වය ලෙස භාවිතා වේ.එබැවින් සෘණ හෝ( OFF) යනුවෙන් හැදින්වෙන්නේ බින්දුව බවත්, ධණ හෝ( ON) යනුවෙන් හැඳින්වෙන්නේ එක බවත්, දත යුතුයි.
- තාර්කික ද්වාර පිළිබද සැලකීමෙදී ඒවා කාණ්ඩ දෙකකට ඒවායේ වොල්ටියතාවය පදනම් කරගෙන බෙදිය හැක.

- තාර්කික දොරටු වර්ග බොහොමයක් තිබේ. ඒවා,
1. NOT
2. AND
3. OR
4. NAND
5. NOR
6. XOR
7. XNOR
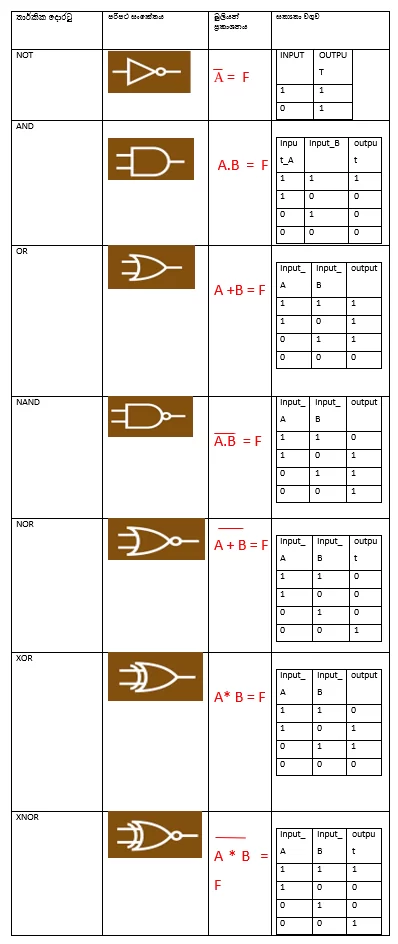
Q: පහත බූලියානු ප්රකාශනයට ගැලපෙන තාර්කික පරිපථය අඳින්න. සත්යතා වගුව ලියා දක්වන්න.
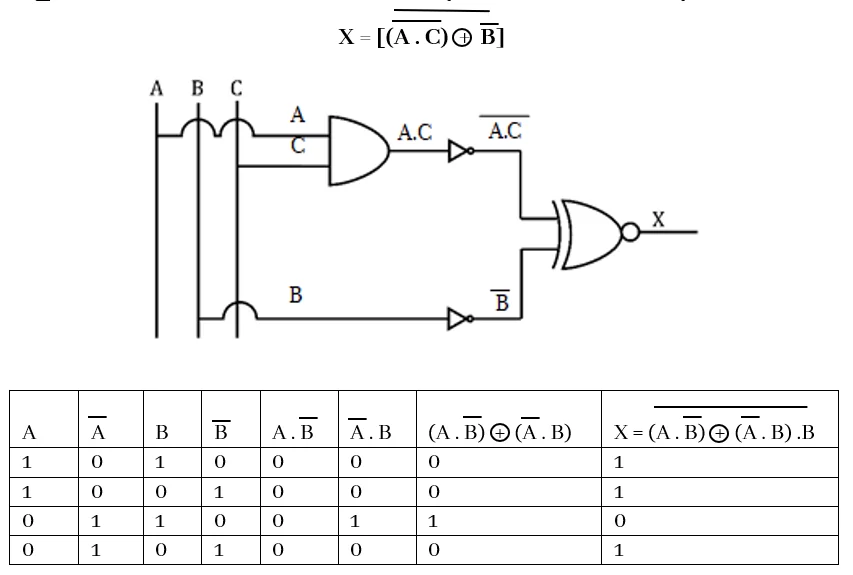
Q: පහත බූලියානු ප්රකාශනයට ගැලපෙන තාර්කික පරිපථය අඳින්න. සත්යතා වගුව ලියා දක්වන්න.
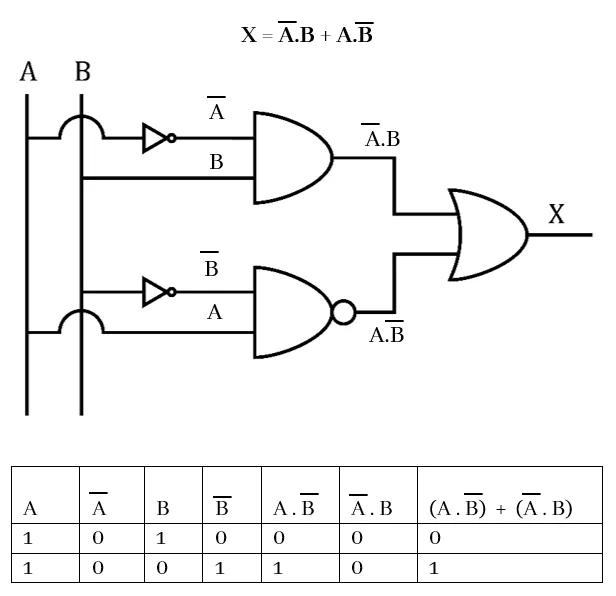
Q: පහත පද්ධතියේ A සහ B ඇසුරින් Z සඳහා බූලියානු ප්රකාශනය ලියන්න. මෙම තාර්කික ද්වාරය සඳහා සත්යතා වගුව අඳින්න.
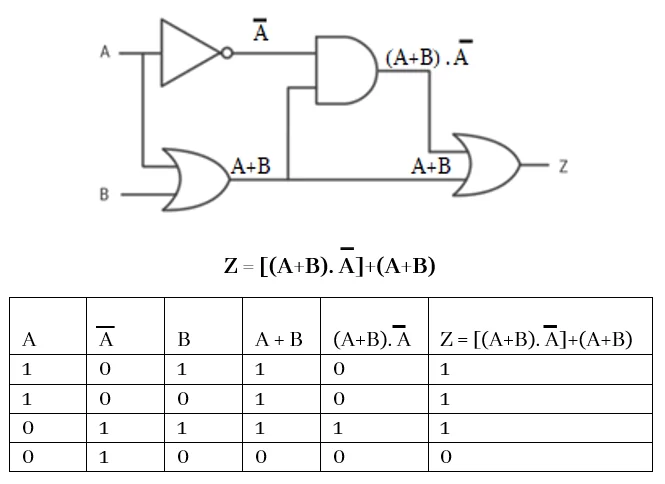
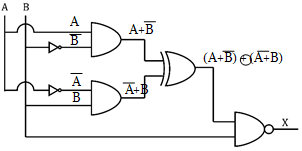
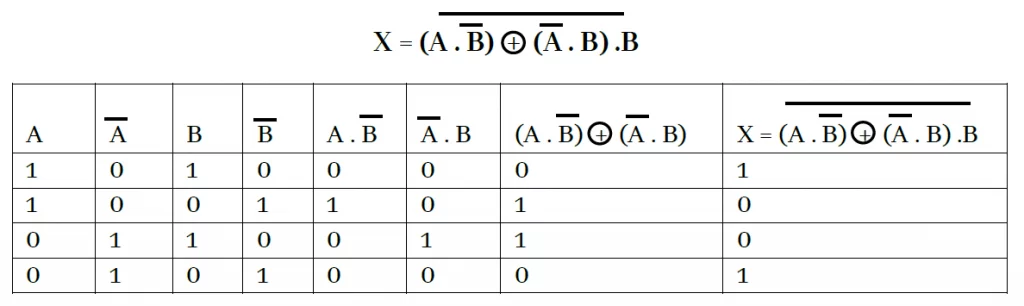
Q: පහත පද්ධතියේ A සහ B ඇසුරින් X සඳහා බූලියානු ප්රකාශනය ලියන්න. මෙම තාර්කික ද්වාරය සඳහා සත්යතා වගුව අඳින්න.
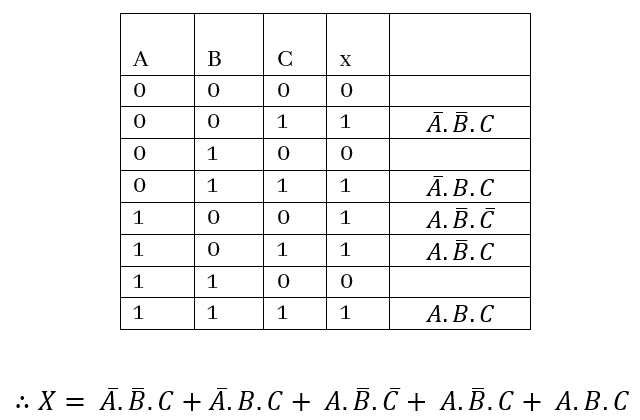
Q: රාත්රී කාලයේදී විදුලිය ඇණ හිටි අවස්තාවකදී ස්වංක්රීයව ක්රියාත්මක වන විදුලි පහනක් දල්වා ගැනීමට සංයුක්ත ද්වාර පරිපථයක් සැලසුම් කර ගත යුතුව ඇත. තවද මෙම බල්බය ඕනෑම බොත්තමක් තද කිරීමෙන්ද දල්වා ගැනීමේ හැකියාව පරිපථයට තිබිය යුතුය. පහත ප්රදාන සංඥා නිපදවා ගත හැකියි සිතන්න.
A = රාත්රී කාලය දැක්වීම (1-රාත්රියේදී, 0 – දහවලේදී)
B = විදුලිය නැති බව දැන්වීම (1-විදුලිය ඇති විට, 0 – විදුලිය නැති විට)
C = බොත්තම තද කල බව දැක්වීම (1-බොත්තම තද කල විට, 0- තද නොකළ විට)
x = 1-බල්බය දැල්වීම, 0-බල්බය නොදල්වීම
නිපදවා ගත යුතු පරිපථයට අදාළ සත්යතා වගුව සහ ප්රකාශනය ලියන්න
මෙහිදී අවශ්යතා වලට අනුව සත්යතා වගුව අඳින්න. එහි ඇති ප්රතිදානය 1 වන අවස්ථා පමණක් සලකන්න. OR ද්වාර ඇසුරින් එම ප්රතිදානය 1 වන අවස්ථා බූලීය අංකනයෙන් ලියා දක්වන්න. ඉන්පසු අවශ්ය අවස්ථාවන්හි ප්රතිදානය 1 වන ලෙස, ඉහත බූලීය අංකනයෙන් ලියන ලද අවස්තා AND ද්වාරයකින් සම්බන්ධ කරන්න. එය අවශ්ය සංයුක්ත ද්වාරය වේ.
SR පිළිපොල [SR Flip Flops] ![]()
SR හෙවත් සැකසූ – යළි සැකසූ(Set – Reset) පිළිපොලක් පහත රූපයේ දක්වා ඇති පරිදි NAND ද්වාර දෙකක් භාවිත කර සාදා ගත හැකි ය.
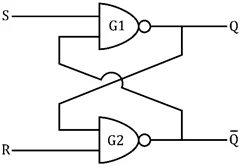
- මෙහි එක් එක් ද්වාරයේ ප්රතිදානය අතෙක් ද්වාරයේ ප්රදානයට සම්බන්ධ කර ඇත. පිළිපොල ස්මෘතිය ලබාගන්නේ මෙම ප්රතිපෝෂණ (Feedback) සම්බන්ධය මගිනි.
- පිළිපොලේ ප්රදාන S සහ R වන අතර එහි ප්රතිදාන P සභ Q වේ. Q̅ යනු Q හි අනුපූරකය යි.
- මෙම පරිපථයට ප්රදාන දෙකක් ඇති නිසා ප්රදාන අවස්ථා හතරක් ඇත. එම ප්රදාන අවස්ථා හතර
(i) S = 0, R = 0
(ii) S = 0, R = 1
(iii) S = 1, R = 0
(iv) S = 1, R = 1 වේ.
- පළමුව S = 1, R = 1 අවස්ථාව සළකා බලමු.
- මෙම අවස්ථාවේ දී Q හි අගය 1 බව උපකල්පනය කරමු. එවිට Q̅ = 0 වේ. මේ අනුව G1 NAND ද්වාරයේ ප්රදාන වන S සහ Q̅ පිළිවෙලින් 1 සහ 0 අගයන් ගන්නා නිසා එහි ප්රතිදානය Q = 1 වේ.
- එනම් G1 වාරයේ ප්රදාන සහ ප්රතිදාන අපගේ උපකල්පනය සමඟ එකඟ වේ. මේ ආකාරයට ම G2 NAND වාරයේ ප්රදාන සහ ප්රතිදාන ද උපකල්පනය සමඟ එකඟ වන බව පෙන්විය හැකි ය.
- දැන් S = 1, R = 1 අවස්ථාවේ දී Q හි අගය 0 බව උපකල්පනය කරමු. එවිට Q̅ = 1 වේ. G1 සහ G2 ද්වාරවල ප්රදාන සහ ප්රතිදාන මෙම උපකල්පනය සමඟ ද එකඟ වන බව පෙන්විය හැකි ය.
- මෙයින් පෙනී යන්නේ S = 1 සහ R = 1 වූ විට SR පිළිපොලහි ප්රතිදාන Q = 1, Q̅ = 0 සහ Q = 0, Q̅ =1 යන අවස්ථා දෙක ම සතාථ කරත බව යි. ඒ අනුව SR පිළිපොලකට S = 1 හා R = 1 ප්රදාන ලබා දී විද්යුත් ජවය සැපයූ විට එහි ප්රතිදානය ඉහත දක්වන ලද ප්රතිදාන අවස්ථා දෙකින් ඕතැම අවස්ථාවකට අහඹු ලෙස පත්විය හැකි අතර එය පත් වන අවස්ථාව නිශ්චිත ලෙස කලින් නිගමනය කළ නොහැකි ය.
- මෙම අවස්ථා දෙක පිළිපොලේ ස්ථායී ප්රතිදාන අවස්ථා ලෙස හැඳින්වේ. පිළිපොල ද්විස්ථායික යනුවෙන් හඳුන්වන්නේ මේ හේතුවෙනි.
S සහ R ප්රදාන වෙනස් කළ විට සිදුවන ප්රතිදාන වෙනස් වීම් දැන් සළකා බලමු.
- S හි අගය තවදුරටත් 1 හි තබා ගනිමින් මොහොතකට R = 0 කරමු. එම මොහොතේ දී පිළිපොලේ ප්රදාන අවස්ථාව S = 1 හා R = 1 වේ. එවිට පිළිපොලේ ප්රතිදාන Q = 1, Q̅ = 0 ස්ථායී අවස්ථාවට පත් වන බව පෙර පරිදි G1 සහ G2 ද්වාරවල ප්රදාන සහ ප්රතිදාන සැසඳීමේ දී පෙනී යයි.
- දැන් S = 0 අගය R = 1 ලෙස වෙනස් කළ ද ප්රතිදානය තවදුරටත් වෙනස් නොවී එම ස්ථායි පිහිටිමේ ම පවතී. මේ අයුරින් පිළිපොලේ ප්රදාන S = 1 සහ R = 1 අවස්ථාවේ පවතින විට මොහොතකට S = 0 කළ විට ප්රතිදාන Q = 0, Q̅ = 1 ස්ථායී අවස්ථාවට පැමිණෙන බව පෙනී යයි.
- එනම් පිළිපොලේ ප්රදාන මොහොතකට S = 0, R = 1 අවස්ථාවට පත් කළ විට එහි ප්රතිදාන Q = 0, Q = 1 වේ. ඉන් පසු R = 0 කළ ද ප්රතිදාන වෙනස් විමකට භාජනය නොවේ.
- මෙයින් පෙනී යන්නේ පිළිපොලේ ප්රතිදාන Q = 0, Q = 1 අවස්ථාවට පත් කිරීම සඳහා මොහොතකට එහි ප්රදාන S = 0 සහ R = 1 කළ යුතු බව සහ ප්රතිදාන Q = 1, Q = 0 බවට පත් කිරීම සඳහා ප්රදාන S = 1 සහ R = 0 කළ යුතු බව යි.
- මෙහි දී ගම්ය වන වැදගත් කරුණක් වන්නේ පිළිපොලේ ප්රතිදානය දෙස බලා එම ප්රතිදාන අවස්ථාවට පත් වීමට පෙර අවසන් වරට පිළිපොලේ පැවති ප්රදාන අවස්ථාව හඳුනා ගත හැකි වීමයි. පිළිපොලේ ප්රතිදානය Q = 1, Q = 0 සැකසූ අවස්ථාව නම්, මෙම අවස්ථාවට පත් වීමට පෙර අවසන් වරට මොහොතකට හෝ එහි S ප්රදානය 1 ව පැවතී බව නිගමනය කළ හැකි වේ.
- එලෙසම පිළිපොලේ ප්රතිදානය S = 0, Q = 1 යළි සැකසූ(Reset) අවස්ථාවේ පවතී නම්, අවසන් වරට 1 වී ඇති ප්රදානය බව නිගමනය කළ හැකි වේ.
- මෙයින් පෙනී යන්නේ අවසන් වරට 1 වූ ප්රදානය මතක තබා ගැනිමේ හැකියාව (ස්මෘතිය) පිළිපොලට ඇති බව යි.
- අනුක්රමික පරිපථවල මූලික අවයවය වන පිළිපොල සතු මෙම ස්මෘතිය හේතුවෙත් අනුක්රමික සංඛ්යාංක පරිපථ වල ද ස්මෘතිය ඇත.
S = 1, R = 1 ප්රදාන අවස්ථාවේ දී පිළිපොලේ ප්රතිදානය නිශ්චිත ව කිව තො හැකි බව කලින් සඳහන් කරන ලදී. එම නිසා SR පිළිපොල යොදා සංඛ්යාංක පරිපථ නිර්මාණය කිරීමේ දී මෙම අවස්ථාව ඇති නො වන පරිදි පරිපථය නිර්මාණය කිරීමට වග බලා ගත යුතු වේ.
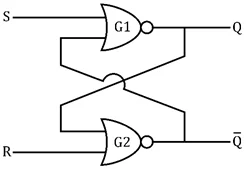
SR පිළිපොලක්, NOR ද්වාර යොදා ගැනීමෙන් ද සකසා ගත හැකි බව පහත රූපයෙන් පැහැදිලි වේ.
ඉදිරියේදී ප්රශ්න ඇතුලත් වන්නේ මෙතනටයි.



