ප්රත්යස්ථතාව හැඳින්වීම
- බාහිර බලයක් යෙදූ විට වස්තුවක දිග , වර්ගඵලය , පරිමාව , හැඩය වැනි රාශියක් වෙනස් වී බාහිර බලය ඉවත් කල විට ඉබේම මුල් තත්වයට පත්වීමේ ගුණය ප්රත්යස්ථතාව ලෙස හැඳින්වේ.
උදා -: රබර් පටියක් ඇද නිදහස් කල විට මුල් තත්වයට පත් වේ
රබර් කුට්ටියක් සම්පීඩනය කොට නිදහස් කල විට මුල් තත්වයට පත්වීම
දුනු පටියක් නවා නිදහස් කල විට ඉබේම මුල් තත්වයට පත් වේ
- බාහිර බලවලට ලක්ව ඇති වස්තූන් ප්රත්යාබල තත්වයක පවතී යැයි කියනු ලැබේ.
- එම බාහිර බලය නිසා කිසියම් වෙනසක් සිදුවී ඇත්නම් එය වික්රියාවකට ලක්ව ඇතැයි කියනු ලැබේ.
- ආතන්ය ප්රත්යාබල යටතේ ආතන්ය වික්රියාවකට බඳුන් වේ.
- දණ්ඩක් , තන්තුවක් හෝ කම්බියක් මත ඉදිරි දිශාව ඔස්සේ බලයක් යෙදූ විට එහි දිග වෙනස් වේ.
දිග වෙනස් වීම විතතිය ලෙසත් යෙදූ බලය නිසා කම්බිය හෝ දණ්ඩ තුළ හටගන්නා බලය ආතතිය ලෙසත් දක්වනු ලැබේ.
දණ්ඩක ඉදිරි දිශාව ඔස්සේ F බලයක් යෙදූ විට e දිග වැඩිවීමක් ලබා දුන්නේ යැයි සලකමු.

- මෙහිදී යම් ස්ථානයකින් කල්පිතව වෙන්කල විට එක් කොටසක් සමතුලිතව පවතින්නේ අප යෙදූ බලය හා අනෙක් කොටසේ අංශු මගින් ඇතිකරන ආකර්ෂණ බල නිසා වේ.
- මෙම ආකර්ෂණ බලවල සම්ප්රයුක්තය ආතතියට සමාන වේ. මේ නිසා ඕනෑම ස්ථානයක ආතතිය සමාන බැවින් ඕනෑම ස්ථානයක අංශුවක් මත ඉදිරි දිශාව ඔස්සේ ක්රියාකරන බලය සමාන වේ.
- මේ නිසා ඕනෑම අංශු 2ක් අතර පරතරය සමාන ලෙස වැඩිවීමෙන් මුළු දිග වැඩිවීම සිදුවේ.
- මේ නිසා මුළු දිග වැඩිවීම පහත සඳහන් සාධක මත රඳා පවති.
- දණ්ඩ සෑදී ඇති ද්රව්යය
- දණ්ඩේ හරස්කඩ වර්ගඵලය
- දණ්ඩේ මුල් දිග
- යෙදූ බලය
ආතන්ය ප්රත්යාබලය
- ඒකක වර්ගඵලයක් මත ආතති බලය වේ.
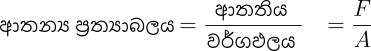
ආතන්ය වික්රියාව
- ඒකක දිගකට විතතිය වේ.
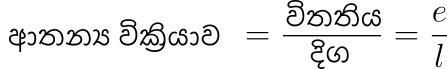
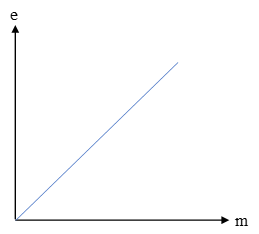
- බොහෝ ද්රව්ය සඳහා සමානුපාතික සීමාව දක්වා ආතන්ය ප්රත්යාබලය, ආතන්ය වික්රියාවට දක්වන අනුපාතය නියතයක් වේ.
- මෙම නියතය අදාළ ද්රව්යයේ යංමාපාංකය ලෙස හැඳින්වේ.

Q: පැත්තක දිග 2 cm වූ සමචතුරස්රාකාර හරස්කඩක් ඇති දිග 1.2 m වූ දණ්ඩකට 200kN බලයක් යෙදූ විට 22cm විතතියක් ඇතිවේ. දණ්ඩේ ආතන්ය ප්රත්යා බලයද, ආතන්ය වික්රියාවද, දණ්ඩ සාදා ඇති ද්රව්යයේ යංමාපාංකය ද සොයන්න.
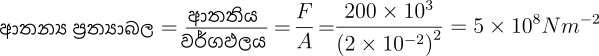
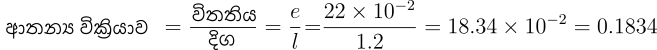
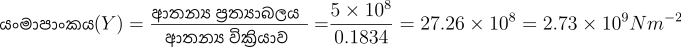
යංමාපාකයේ අර්ථ දැක්වීම
- අදාළ ද්රව්යයෙන් සාදන ලද ඒකක හරස්කඩ වර්ගඵලයක් ඇති ඒකාකාර දණ්ඩක ඒකක දිගකට ඒකක විතතියක් සමානුපාතික සීමාව තුළ දී ඇතිකරන බලය ද්රව්යයේ යංමාපාකය ලෙස හැඳින්වේ .
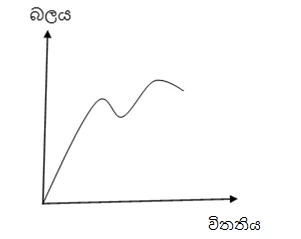
- වානේ වැනි ද්රව්යයක කම්බියක් ගෙන ක්රමයෙන් බලය වැඩිකොට විතතිය මැන විතතිය ඉදිරියෙන් බලය හෝ වික්රියාව ඉදිරියෙන් ප්රත්යාබලය ප්රස්තාර ගත කල විට පහත දැක්වෙන ප්රස්තාර ලැබේ.
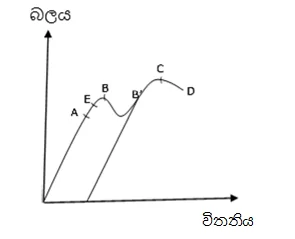
A- සමානුපාතික සීමාව
B- අවනති ලක්ෂ්යය
C- භේදක ලක්ෂ්යය
D- කැඩීම
E- ප්රත්යස්ථ සීමාව
A- සමානුපාතික සීමාව
- A ලක්ෂයට අදාල බලය දක්වා බලය ක්රමයෙන් වැඩි කරන විට ඊට සමානුපාතිකව විතතියද වැඩිවේ.
හුක් නියමය
සමානුපාතික සීමාව තුළ යොදන බලය ඇතිකරන විතතියට අනුලෝමව සමානුපාතික වේ.
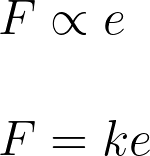
Q: k යන සමානුපාතික නියතයේ අගය 6×1012 වන ද්රව්යයකින් සැදී කම්බියක් 2×10-2 mm විතතියක් ලබා දීමට සමත් වන්නේ කවර බලයක්ද?
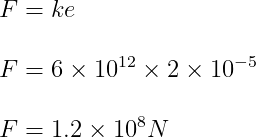
E- ප්රත්යාස්ථ සීමාව
- E ලක්ෂයට අනුරූප බලය දක්වා බලය ක්රමයෙන් වැඩි කොට බලය ඉවත් කල විට කම්බිය මුලින් තිබූ තත්වයට පත් වේ. නමුත් Aහා E අතරද හුක් නියමය පිලිනොපදී.
B- අවනති ලක්ෂ්යය
- ප්රත්යාස්ථ සීමාව ඉක්මවූ විට B වැනි ලක්ෂයකට අනුරූපව කම්බිය මත අංශු එකමත එක ලිස්සීම අරඹයි.
- මෙය සුවිකාර්ය වීම ලෙස හැඳින්වේ.
- මැටි , Clay වැනි ද්රව්ය ආරම්භයේ සිටම සුවිකාර්ය වේ.
- වීදුරු වැනි ද්රව්ය ප්රත්යාස්ථ සීමාව ඉක්මවා සුවිකාර්ය නොවේ.
- පෘෂ්ඨ මත අංශු එකමත එක ලිස්සීමේදී අණු බන්ධන බිඳෙන නිසා ඒ සඳහා කාර්ය කිරීමට යොදන බලයෙන් කොටසක් වැයවන නිසා කම්බියේ ආතතිය අඩුවේ.
- B’ වැනි ලක්ෂයකට අනුරූප බල යෙදීමෙන් පසු බලය ඉවත් කරන විට B’E’ වැනි ප්රස්තාරයක් අනුගමනය කරයි.
- එනම් OE’ ට සමාන ස්ථිර විතතියක් ඇති
C- භේදක ලක්ෂ්යය
- C ලක්ෂයට අනුරූප බලය යෙදූ විට කම්බිය සිහින් වී D වැනි ලක්ෂයකදී කැඩී යයි.
- කම්බිය කැඩීමේදී අණු එකිනෙක වෙන්වන නිසා ඒ සඳහා කාර්ය කිරීමට බලයෙන් කොටසක් වැයවන බැවින් කැඩෙන අවස්ථාවේ ආතතිය යෙදූ බලයට වඩා අඩු අගයක් ගනී.
Q: දිග 1.6 m සහ අරය 1 mm වන වානේ කම්බියක ඉහල කෙලවර අචල ආධාරකයකට සම්බන්ධ කර පහල කෙලවරට 20 kg ක භාරයක් යොදනු ලැබේ. සමානුපාතික සීමාව ඉක්ම නොවූයේ යයි සලකා කම්බියේ විතතිය සොයන්න. (වානේ වල යංමාපාංකය 2 x 1011 Nm-2 වේ.)
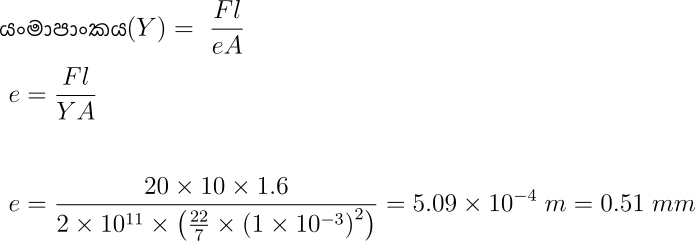
වික්රියා විභව ශක්තිය
- කම්බියක් මත බලයක් යෙදූ විට කම්බියේ දිග වැඩිවේ. එනම් බලය චලිත වේ.
- බලය මගින් කාර්ය කරයි.
- එම කාර්ය කම්බිය තුල ශක්තිය ලෙස ගබඩා වේ.
- එම ශක්තිය වික්රියා විභව ශක්තිය ලෙස හැඳින්වේ.
- මෙහිදී බලය ක්රමයෙන් වැඩි කරන නිසා මුළු බලයට මුළු විතතියට සමාන දුරක් චලිත නොවේ
- මේ නිසා මධ්යන්ය බලය මගින් කරනු ලබන කාර්ය සලකනු ලැබේ.
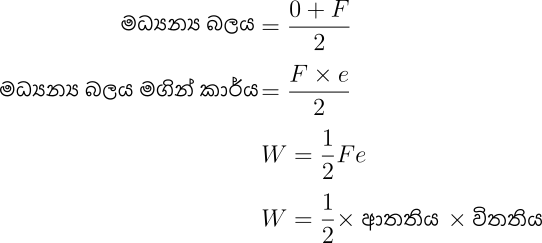
Q: වානේ කම්බියක එක කෙළවරක් අචල ආධාරකයකට බැඳ එහි නිදහස් කෙලවරට 200N ක බලයක් යොදා එය ඉවතට ආදී විට එහි ඇති වූ විතතිය 5mm වේ. කම්බියේ ගබඩා වී ඇති ශක්තිය කොපමණද?

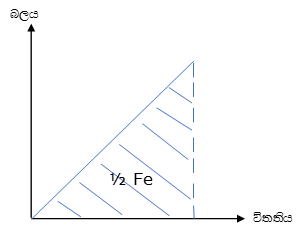
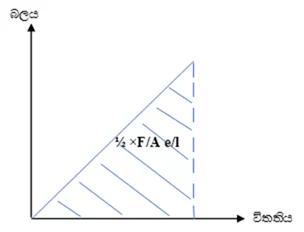
- එනම් විතතිය ඉදිරියෙන් බලය ප්රස්තාරගත කල විට ප්රස්තාරයත් x අක්ෂයත් අතර වර්ගඵලයෙන් ගබඩා වන ශක්තිය ලැබේ.
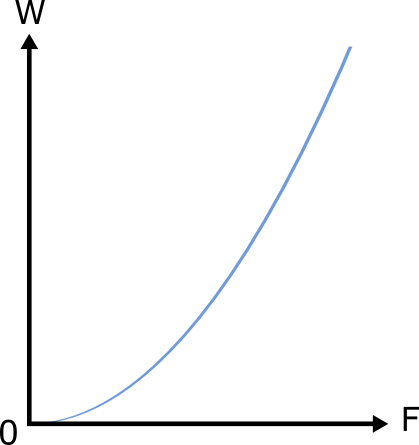
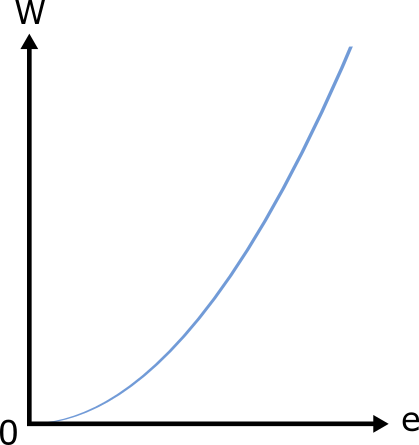
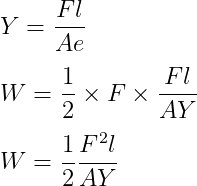
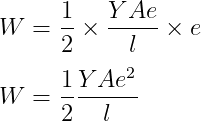
Q: එක්තරා ද්රව්යයකින් සාදන ලද කම්බියක දිග 2m ද, සමචතුරස්රාකාර හරස්කඩේ පැත්තක දිග 5cm ද වේ. එය සාදා ඇති ද්රව්යයේ යංමාපාකය 2.5×109 Nm-2 වේ. යම් බලයක් එයට යොදා එය ඇද්ද විට එහි ඇති වූ විතතිය 0.05 mm වේ නම් එවිට එහි ගබඩා වී ඇති වික්රියා විභව ශක්තිය කොපමණද?
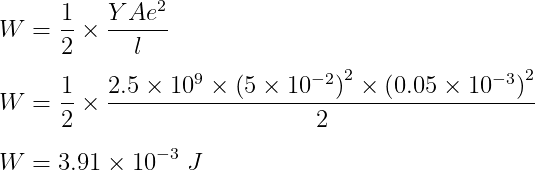
ඒකක පරිමාවක ගබඩාවන ශක්තිය
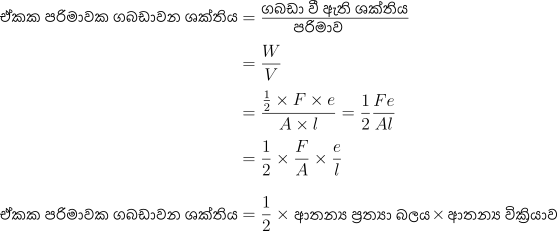
Q: එක්තරා ලෝහයක යංමාපාංකය 2 x 1011 Nm-2 වේ. එහි එක් කෙළවරක් වහලයකට සම්බන්ධ කර අනෙක් කෙළවරෙන් 10kg භාරයක් එල්ලා ඇත. එවිට කම්බියේ ඒකක පරිමාවක ගබඩා වන විභව ශක්තිය සොයන්න. (කම්බියේ අරය 0.2 mmවේ.)
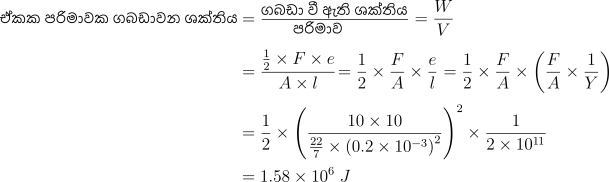
- වික්රියාවට ඉදිරියෙන් ප්රත්යාබලය ප්රස්තාරයත් x අක්ෂයත් අතර වර්ගඵලයෙන් ඒකක පරිමාවක ගබඩාවන ශක්තිය ලැබේ.
ලෝහ කම්බියක යංමාපාංකය සෙවීම
උපකරණ
- එකම ද්රව්යයෙන් සාදන ලද එකම දිග ඇති සිහින් ඒකාකාර කම්බි 2 ක්
- ප්රධාන පරිමාණයක්
- ව’නියර් පරිමාණයක්
- ½kg පඩි කට්ටලයක්
- අමතර භාරයක්
- මීටර් රූලක්
- මයික්රෝමීටර ස්කුරුප්පු ආමානයක්
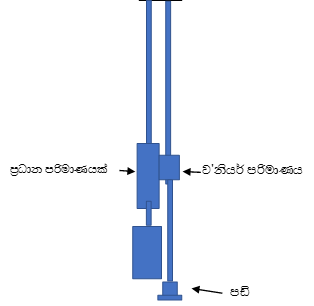
- එකම ආධාරකයක කම්බි දෙකම එල්ලන්න .
- එක් කම්බියක ප්රධාන පරිමාණය එල්ලා එමගින් අමතර භාරය එල්ලීමෙන් කම්බිය ඇදී පවතින සේ සකස් කරගන්න .
- අනෙක් කම්බියේ ව’නියර් පරිමාණය එල්ලන්න. ව’නියර් පරිමාණයෙන් බර යොදන තැටිය එල්ලන්න.
- තැටියට ආරම්භයේදි 1kg පමණ පඩියක් යොදා ව’නියරයේ ශූන්ය සලකුණෙන් දක්වන පාඨාංකය ප්රධාන පරිමාණයෙන් හා ව’නියර් පරිමාණයෙන් කියවන්න.
- ½kg ක පඩියක් යොදා නැවත ව’නියරයේ ශූන්ය සලකුණෙන් දක්වන පාඨාංකය කියවාගෙන ආරම්භක පාඨාංකය අඩුකොට විතතිය ලබාගන්න.
- ½kg බැගින් බර වැඩි කරමින් ඉහත ආකාරයට පරීක්ෂණය කොට අදාළ මිනුම් ලබාගන්න .
- නැවත භාරය ඉවත් ඉවත් කරමින්ද එක් එක් භාරයට අනුරූප පාඨාංක කියවාගෙන විතතිය ලබාගන්න.
- කම්බියේ ස්ථාන කිහිපයකින් විෂ්කම්භය මැන ගන්න.
වාදය
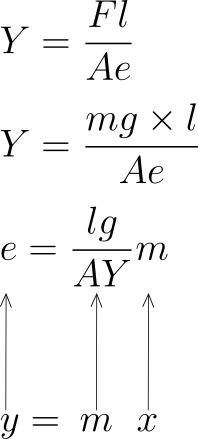
| යෙදූ පඩිවල ස්කන්ධය | mo | m1 | m2 |
| ව’නියරය දක්වන පාඨාංකය | x0 | x1 | x2 |
| සඵල භාරය | m1 – mo | m2 – mo | |
| විතතිය | x1 – x0 | x2 – x0 |
- මෙහිදී කම්බිය 2.5mm පමණ දිගින් විය යුතු අතර කම්බියේ විෂ්කම්භය 0.5mm හෝ 1mm ප්රමාණයේ විය යුතුය.
- මෙහිදී සිහින් දිග කම්බියක් යොදාගන්නේ වැඩි විතතියක් ඇතිකොට එම මිනුමේ නිරවද්යතාවය වැඩි කරගැනීමට වේ.
- ව’නියර් මූලධර්මය යොදාගන්නේ විතතිය කුඩා මිනුමක් නිසා මිනුම නිරවද්යව ගැනීමට වේ.
- මෙහි ඇති කුඩාම විතතිය හා විෂ්කම්භය නිසා ඒවා වැඩිම නිරවද්යතාවයෙන් ගත යුතුය.
- එකම ආධාරකයක එල්ලීමෙන් බර යෙදීමේදී ආධාරකය පහත් වූ විට ප්රධාන හා ව’නියර් පරිමාන එකම ප්රමාණයකින් පහත් වන නිසා විතතියට දෝෂයක් ඇති නොවේ.
- එකම දිග ඇති එකම ද්රව්යයෙන් සැදි කම්බි දෙකක් යොදාගත්විට උෂ්ණත්වය වෙනස් වන විට සිදුවන ප්රසාරණය නිසා ප්රධාන හා ව’නියර් පරිමාණ එකම ප්රමාණයකින් වෙනස් වන නිසා දෝෂයක් ඇති නොවේ.
- මෙහිදී භාරය එක් කරමින් එක් වතාවක් ද, භාරය ඉවත් කරමින් තවත් වතාවක්ද පාඨාංක ලබාගන්නේ ප්රත්යාස්ථ සීමාව ඉක්මවා ඇත්දැයි බැලීමටත්, නැම්මක් දිගහැරීම හෝ සම්බන්ධක ලිස්සීමක් සිදුවී ඇත්දැයි බැලීමටත් වේ.
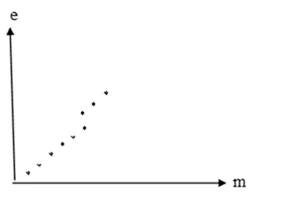
නැම්මක් දිගහැරීම හෝ සම්බන්ධක ලිස්සූ විට
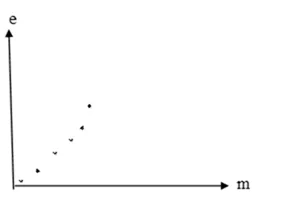
ප්රත්යාස්ථ සීමාව ඉක්මවූ විට
- මෙවැනි අවස්ථා වල රේඛීයව පවතින එක් කොටසක් පමණක් යොදාගෙන ගණනය කිරීම් කළ හැකිය.
ඔබට මෙම කොටස වීඩියෝ මගින් අධ්යයනය කිරීමට :



