භ්රමණ චලිතය
- කිසියම් අංශුවක් යම් ලක්ෂයක සිට නිශ්චිත දුරක් පවත්වා ගනිමින් එය චලිත වේ නම් එය කෝණික චලිතයකි.
කෝණික විස්ථාපනය
- කෝණික චලිතයේ යෙදෙන අංශුවක් කේන්ද්රය ආපාතනය කරන කෝණය රේඩියනය කෝණික විස්ථාපනය නම් වේ.
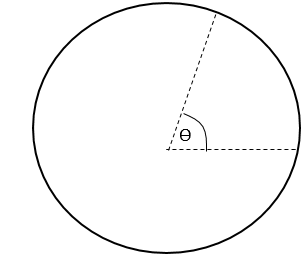
- අංශුවක් පූර්ණ වටයක් සම්පූර්ණ කළ විට කෝණික විස්ථාපනය 2𝜋 rad වේ.
- කෝණික විස්ථාපනය තුළ දෛශික මෙන්ම අදිශ ගුණ ද ඇත.
- වෘත්තයක අරය ට සමාන චාප දිගකින් කේන්ද්රය ආපාතනය කරන කෝණය ‘රේඩියනය’ වේ.
𝜋 rad = 180°
2𝜋 rad = 360°
- 2𝜋r දිගකින් කේන්ද්රය ආපාතනය කරන කෝණය = 2𝜋 rad
- ඒකක දිගකින් කේන්ද්රය ආපාතනය කරන කෝණය = 2𝜋 ÷ 2𝜋r
- S දිගකින් කේන්ද්රය ආපාතනය කරන කෝණය = (2𝜋 ÷ 2𝜋r) × S
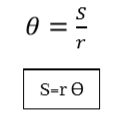
- S දිග චාප කොටසකින් අරය r වෘත්තයක කේන්ද්රය ආපාතිත කෝණය, ϴ විට ඉහත සමීකරණයෙන් ලැබේ.
- භ්රමණයක් නොමැති අවස්ථාවකදී මනිනු ලබන කෝණය (උදා: ත්රිකෝණයක කෝණය) අදිශයකි.
- භ්රමණයක් පවතී නම් එම කෝණය දෛශිකයකි. එහි දිශාව දකුණත් නියමයෙන් ලැබේ.
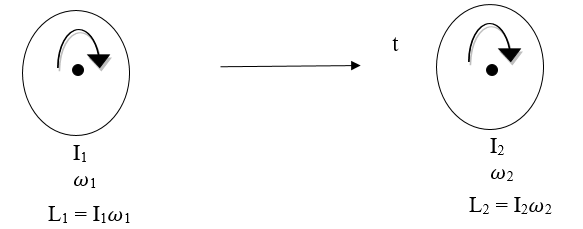
ආවර්ත කාලය (T)
- එක් සම්පූර්ණ වටයක් භ්රමණය වීමට ගතවන කාලය වේ.
භ්රමණ සංඛ්යාතය (f)
- තත්පරයකදී භ්රමණය වන වාර ගණන භ්රමණ සංඛ්යාතය’ වේ.
- යම් වස්තුවක භ්රමණ සංඛ්යාතය f නම්, වට f ගණනක් භ්රමණය වීමට ගතවන කාලය = 1s
- වට 1ක් භ්රමණය වීමට ගතවන කාලය = 1/f
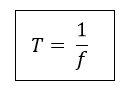
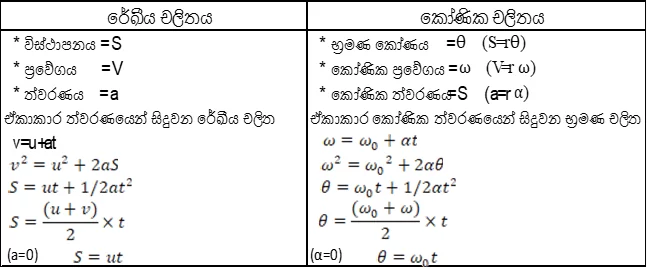
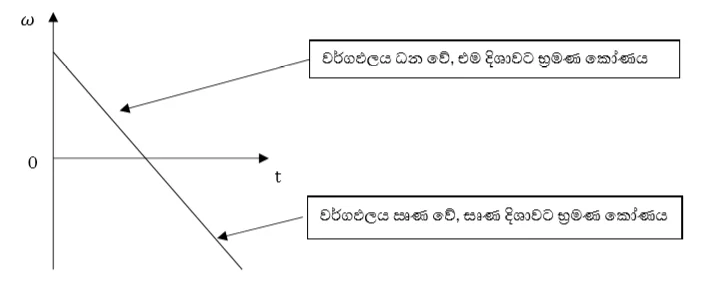
- රේඛීය චලිතය කදී කාලයත් සමඟ වස්තුව ගමන් ගන්නා දුර වෙනස් වේ, භ්රමණය චලිතය කදී නම් කාලයත් සමඟ භ්රමණය වන කෝණය වෙනස් වේ.
- සලකන යම් දිශාවකට භ්රමණ කෝණය ධන නම්, ඊට ප්රතිවිරුද්ධ දිශාවට භ්රමණ කෝණය ඍණ වේ.
කෝණික ප්රවේගය (ω) – දෛශික
- කෝණික විස්ථාපනය වෙනස් වීමේ ශීඝ්රතාවය කෝණික ප්රවේගය නම් වේ.
- එනම් ඒකක කාලයකදී භ්රමණය වූ කෝණයයි.
- t කාලයකදී භ්රමණය වූ කෝණය ϴ නම්,
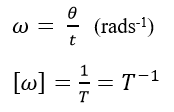
- නමුත්,
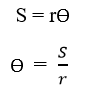
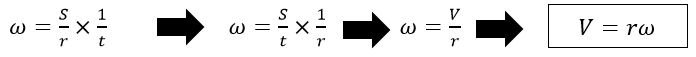
- අරය r වූ වෘත්තාකාර පථයක, ω කෝණික ප්රවේගයකින් භ්රමණය වන අංශුවක ස්පර්ශීය (රේඛීය) ප්රවේගය වන V ඉහත සමීකරණයෙන් ලැබේ.
- භ්රමණ අක්ෂය සිට අංශුවට ඇති දුර අනුව රේඛීය ප්රවේගය වෙනස් වූවද කෝණික ප්රවේගය වෙනස් නොවේ.
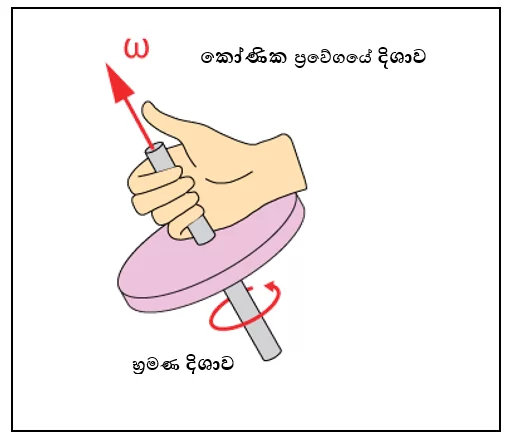
- කෝණික ප්රවේගය දෛශිකයක් වන්නේ භ්රමණ කෝණය දෛශිකයක් නිසාය. එබැවින් කෝණික ප්රවේගයේ දිශාවද දකුණත් නියමයෙන් ලැබේ.
දකුණත් නියමය
- දකුණු අතේ ඇඟිලි වලින් වස්තුවක භ්රමණ දිශාව පෙන්වනු ලබන විට එයට ලම්බක තලයක ඇති මහපට ඇඟිල්ලෙන් කෝණික ප්රවේගයේ දිශාව ලැබේ.
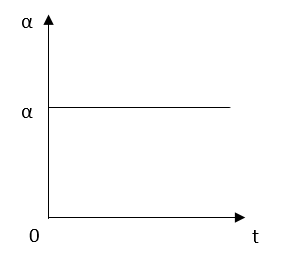
කෝණික ත්වරණය (α) – දෛශික
- කෝණික ප්රවේගයේ වෙනස්වන ශීඝ්රතාවය කෝණික ත්වරණය යි.
- t කාලයකදී සිදුවූ කෝණික ප්රවේග වෙනස Ω නම්,

- නමුත්,
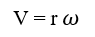

- අරය r වන වෘත්තාකාර පථයක α කෝණික ත්වරණයකින් භ්රමණය වන අංශුවක රේඛීය (ස්පර්ශීය) ත්වරණය වන a ඉහත සමීකරණයෙන් ලැබේ.
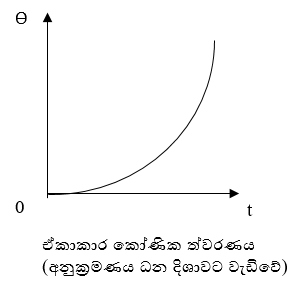
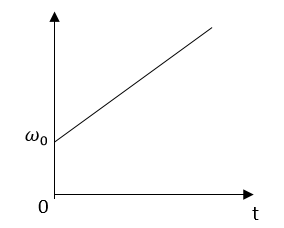
ω ආරම්භක හා t කාලයකදී වූයේනම්,
ω0 = ආරම්භක කෝණික ප්රවේගය
ω = අවසාන කෝණික ප්රවේගය
α = කෝණික ත්වරණය


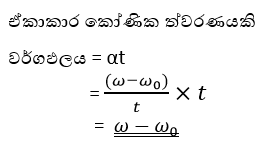
භ්රමණ අවස්ථිතිය හෙවත් අවස්ථිති ඝූර්ණය
- නිශ්චලව පවතින වස්තුවක් භ්රමණය කිරීමට උත්සහ කිරීමේදීත්, භ්රමණය වන වස්තුවක් නිශ්චල කර ගැනීමට උත්සාහ කිරීමේදීත් ඒ සඳහා දක්වන්නාවූ අකමැත්ත භ්රමණය අවස්ථිතිය හෙවත් අවස්ථිති ඝූර්ණය වේ.
- භ්රමණය චලිතය විස්තර කරන විට යොදා ගන්නා අවස්ථිති ඝූර්ණය පදය රේඛීය චලිතය විස්තර කරන විට යොදා ගන්නා රේඛීය අවස්ථිතිය ට අනුරූප වේ.
- අවස්ථිති ඝූර්ණය කෙරෙහි,
- වස්තුවේ ස්කන්ධය
- ස්කන්ධ ව්යාප්තිය, බලපායි.
- වස්තුවක ස්කන්ධය වැඩිවනවිට අවස්ථිති ඝූර්ණය වැඩිවන අතර භ්රමණ අක්ෂය සිට ස්කන්ධ ව්යාප්තියේ දුර වැඩිවනවිට අවස්ථිති ඝූර්ණය වැඩි වේ.
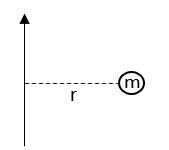
- භ්රමණ අක්ෂයේ සිට r දුරකින් පිහිටි ලක්ෂයක m ස්කන්ධයක් පවතින විට අවස්ථිති ඝූර්ණය පහත පරිදි වේ.
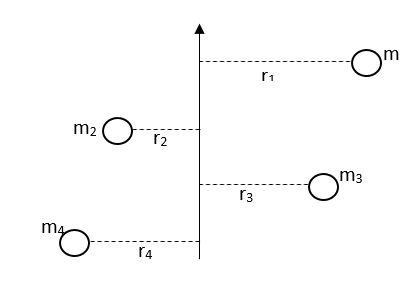
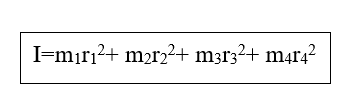
- අවස්ථිති ඝූර්ණය අදිශ රාශියක් බැවින් ස්කන්ධ ව්යාප්තියක අවස්ථිති ඝූර්ණය ඉහත පරිදි වේ.
- දෘඩ වස්තුවක කුඩා ලාක්ෂාකාර අංශුන් අති විශාල සංඛ්යාවක් ඇති බැවින් සලකන ලබන අක්ෂයක් වටා අවස්ථිති ඝූර්ණය ඉහත පරිදි එකතු කොට ලබා ගත යුතුය.
- ස්කන්ධය m හා අරය r වන සිහින් මුදුවක කේන්ද්රය හරහා ගමන් කරන අක්ෂයක් වටා අවස්ථිති ඝූර්ණය,
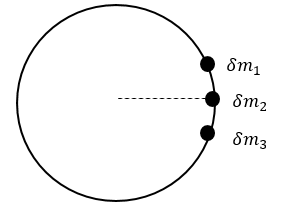
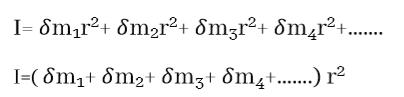
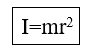
- ස්කන්ධය m හා අරය r වන වෘත්තාකාර තැටියක කේන්ද්රය හරහා ගමන් කරන අක්ෂයක් වටා අවස්ථිති ඝූර්ණය,
- මෙහිදී කේන්ද්රයේ සිටම අංශු පවතින බැවින් එකෙක් අංශුවට පවතින දුර (අක්ෂයේ සිට) වෙනස් වේ. එම නිසා අවස්ථිති ඝූර්ණය සෙවීමත් තරමක් සංකීර්ණය.
- අනුකලනය භාවිතා කොට අවස්ථිති ඝූර්ණය සෙවීමෙන් පහත ප්රතිඵලය ලැබේ.
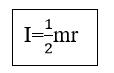
- පහත ප්රතිපලද අනුකලනය භාවිතයෙන් ගනු ලබයි.
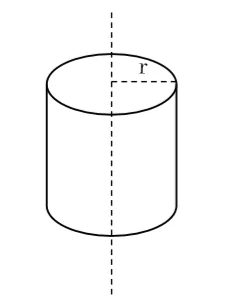
- ස්කන්ධය m හා අරය r වන සිලින්ඩරයක කේන්ද්රය හරහා ගමන් කරන සිරස් අක්ෂයක් වටා අවස්ථිති ඝූර්ණය,
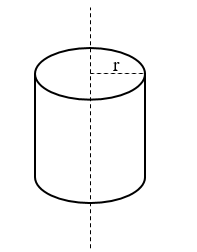
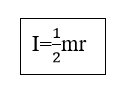
- ස්කන්ධය m හා අරය r වන කුහර සිලින්ඩරයක අවස්ථිති ඝූර්ණය,
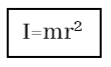
- ස්කන්ධය m හා අරය r වන ඒකාකාර ඝන ගෝලයක අවස්ථිති ඝූර්ණය,
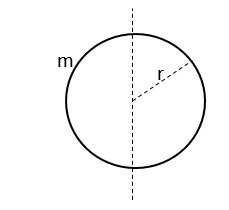
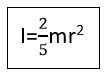
- ස්කන්ධය m හා අරය r වන ඒකාකාර කුහර ගෝලයක අවස්ථිති ඝූර්ණය
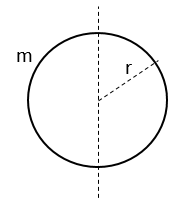
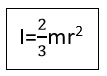
- ස්කන්ධය m හා දිග L වන ඒකාකාර දණ්ඩක ගුරුත්ව කේන්ද්රය හරහා හා කෙළවරක් හරහා ගමන් කරන අක්ෂයක් වටා අවස්ථිති ඝූර්ණය,
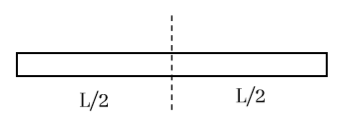
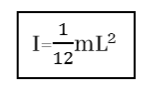
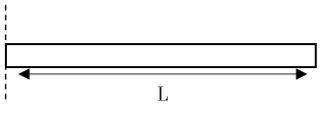
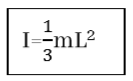
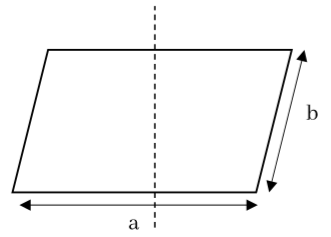
- ස්කන්ධය m හා දිග a හා පළල b වන සෘජුකෝණාස්රාකාර තහඩුවක ගුරුත්ව කේන්ද්රය හරහා ගමන් කරන අක්ෂය වටා අවස්ථිති ඝූර්ණය,
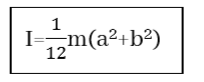
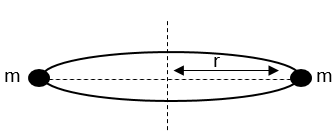
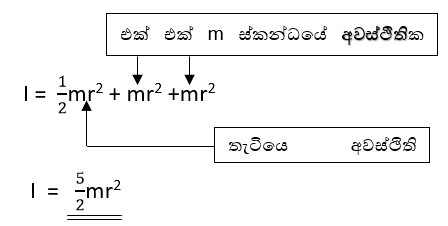
- ස්කන්ධය m හා අරය r වන වෘත්තාකාර තැටියක පරිධිය මත විෂ්කම්භය දෙකෙළවර m ස්කන්ධ දෙකක් තබා ඇත. කේන්ද්රය හරහා යන අක්ෂය වටා අවස්ථිති ඝූර්ණය පහත පරිදි ලබාගත හැක,
අවස්ථිති ඝූර්ණය සම්බන්ධ සමාන්තරීක්ෂ නියමය (වැඩිදුර)
- කිසියම් වස්තුවක ගුරුත්ව කේන්ද්රය හරහා ගමන් කරන අක්ෂය වටා අවස්ථිති ඝූර්ණය දන්නේ නම් ඊට සමාන්තර වෙනත් අක්ෂයක් වටා අවස්ථිති ඝූර්ණය පහත පරිදි වේ.
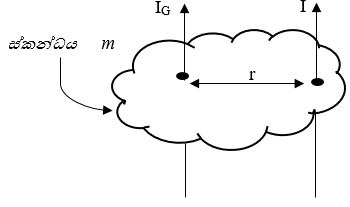

- මේ අනුව වස්තුවක් හරහා සමාන්තර අක්ෂ කිහිපයක් සැලකූවිට ගුරුත්ව කේන්ද්රය හරහා යන අක්ෂය වටා අඩුම අවස්ථිති ඝූර්ණය පවතී.
- ඒ අනුව,
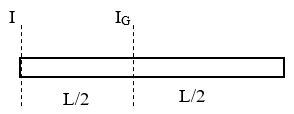
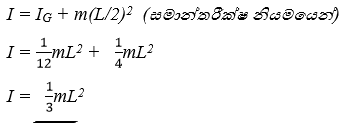
විභ්රමණ අරය (වැඩිදුර)
- වස්තුව කිසි යම් අක්ෂයක් වටා ඇති කරන අවස්ථිති ඝූර්ණය ම ලබා දෙන ආකාරයට වස්තුවේ ස්කන්ධයට සමාන ලක්ෂීය ස්කන්ධයක් භ්රමණ අක්ෂය සිට තැබිය යුතු දුර විභ්රමණ අරය වේ.
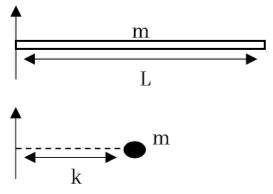
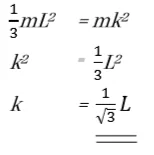
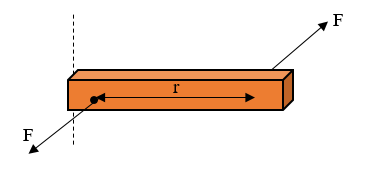
වස්තුවක් භ්රමණය කිරීමට පැවතිය යුතු අවශ්යතාවය
- වස්තුවක් භ්රමණය කිරීමට කිසියම් බලයක් මගින් බල යුග්මයක් හෙවත් ව්යවර්තයක් ඇති කළ යුතුය.
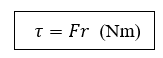
කෝණික ගම්යතාවය
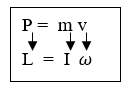
- යම් අක්ෂයක් වටා භ්රමණය වන අංශුවක කෝණික ගම්යතාවය අර්ථ දක්වන්නෙ එහි රේඛීය ගම්යතාවයේ භ්රමණඅක්ෂය වටා ඝූර්ණය ලෙසයි.
- වස්තුවක් අංශු විශාල ගණනාවකින් සමන්විත බැවින්, මෙලෙස අවස්ථිති ඝූර්ණයේත්, කෝණික ප්රවේගයේත් ගුණිතයෙන් එය ලබා ගනී.
- එය රේඛීය ගම්යතාවයට අනුරූපව අවස්ථිති ඝූර්ණයේත් කෝණික ප්රවේගයේත් ගුණිතයක් ලෙස පහත පරිදි ලිවිය හැක.
- මෙය දෛශික රාශියක් වන අතර එහි දිශාව කෝණික ප්රවේගය දිශාවෙන් ලබාදෙයි.( කෝණික ප්රවේගය දිශාව සුරත් නියමයෙන් ලබාගනී)
කෝණික ගම්යතා සංස්ථිති මූලධර්ම
- යම් වස්තුවක් හෝ වස්තු පද්ධතියක් මත යම් අක්ෂයක් වටා බාහිර ව්යාවර්තයක් ක්රියා නොකරයි නම් එම අක්ෂය වටා වස්තුවේ හෝ වස්තු පද්ධතියේ කෝණික ගම්යතාව සංස්ථිතික වේ.
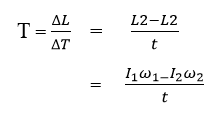
කෝණික ගම්යතා සංස්ථිතියේ යෙදීම්
- භ්රමණ වේදිකාවක් මත සිටින දෑතට ස්කන්ධ දෙකක් ගත් මිනිසෙක් ස්කන්ධ දෙක ඈත් කොට භ්රමණය වන අවස්ථාවේ දී ස්කන්ධ දෙක ළං කරණු ලැබුවහොත් භ්රමණ වේගය වැඩිවේ. මෙහිදී පද්ධතිය මත බාහිර බල ඝූර්ණයක් නොයෙදෙන නිසා ස්කන්ධ ළං කිරීමේදී අවස්ථිති ඝූර්ණය(I) අඩු වන විට කෝණික ප්රවේගය (ω) වැඩි වී කෝණික ගම්යතාව නියතව තබා ගනියි.
- පිහිනුම් වේදිකාවෙන් (Diving Board) පනින ක්රීඩකයෙකු දෙ අත් හා ඇඟ හකුලුවා ගනයි. එවිට I අඩු වන නිසා විශාල වට ගණනක් ඉහළදී භ්රමණය විය හැකි වේ.
- කෝණික ගම්යතාව දෛශිකයක් නිසා එහි විශාලත්වය මෙන්ම දිශාවද ආරක්ෂා කර ගැනීම වැදගත් වේ.
- බයිසිකලයක් වේගයෙන් පදින විට සංතුලනය කර ගැනීම පහසුය.
- කුරුම්බා ගෙඩියක් කරකවා පහලට අතහැරීම.
- තුවක්කුවකින් පිට වන උණ්ඩයක් භමණය වෙමින් ඉදිරියට ගමන් කරන විට ඉලක්කය ගැනීම පහසු වේ.
4. හෙලිකොප්ටරයක අවර පෙති භ්රමණය කිරීමට ඇතුලත ඇති එන්ජිමෙන් බල යුග්මයක් යෙදෙන විට ඊට ප්රතිවිරුද්ධ බල යුග්මයක් හෙලිකොප්ටරය මත යෙදේ. අවර පෙති එක් අතකට භ්රමණය වන විට හෙලිකොප්ටරය ප්රතිවිරැද්ධ අතට භ්රමණය වීමෙන් කෝණික ගම්යතාවය සංස්ථිතික කර ගනියි.
5.
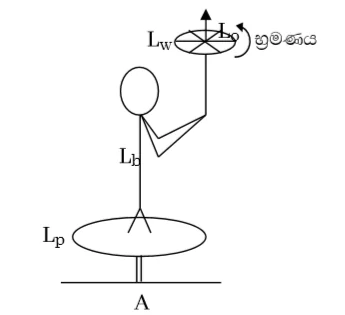
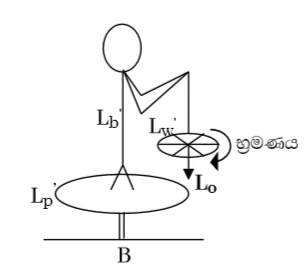
Lb = ළමයාගේ කෝණික ගම්යතාවය
Lc = තැටියේ කෝණික ගම්යතාවය
Lw = රෝදයේ කෝණික ගම්යතාවය
A රුපයේ පරිදි තිරස්ව භ්රමණය විය හැකි තැටිය මත සිට ගෙන සිටින ලමයෙකුගේ අතේ සුමට අක්ෂයක් වටා භ්රමණය වන බයිසිකල් රෝදය ඇත.
A හිදී ලමයා හා තැටිය නිශ්චල නිසා,
Lp = 0 හා Lb = 0
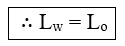
ඉන්පසු රූපයේ පරිදි ලමයා එම රෝදය 1800 කින් භ්රමණය කරවන ලදි. එවිට ලමයා සහිත තැටිය රෝදයේ නව භ්රමණ දිශාවට පතිවිරුද්ධ දිශාවට භ්රමණය වන බව නිරීක්ෂණය වේ.
මෙහිදී භ්රමණ අක්ෂය වටා බාහිර බල ඝූර්ණයක් නොයෙදෙන බැවින් කෝණික ගම්යතා සංස්ථිති නියමය යෙදිය හැක.
කෝණික ගම්යතා සංස්ථිතිට අනුව,
පද්ධතියේ පෙර මුලු කෝණික ගම්යතාව = පසු මුලු කෝණික ගම්යතාව
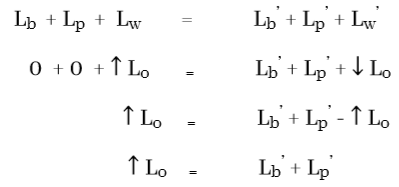
මේ අනුව ලමයා සහිත තැටිය බයිසිකල් රෝදයේ පෙර කෝණික ගම්යතාවය මෙන් දෙගුණයක කෝණික ගම්යතාවයකින් භ්රමණය වේ.
6. සූර්යයා වටා ග්රහ වස්තූන්ගේ චලිතය :-
m ස්කන්ධයක් ඇති ග්රහයෙකු සූර්යයා වටා ඉලිප්සාකාර පථයක ගමන් කරයි.
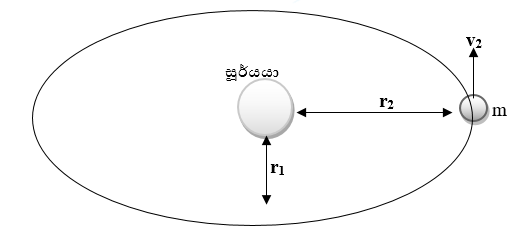
ග්රහයා සඳහා කෝණික ගම්යතා සංස්ථිතියට අනුව,

පෙර කෝණික ගම්යතාව = පසු කෝණික ගම්යතාව
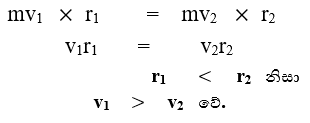
මේ අනුව පැහදිලි වන්නේ සූර්යයා ට ආසන්නව ග්රහයෙකු ගමන් කරනා විට වැඩි වේගයකින් ද, සූර්යයා ට ඈතින් ග්රහයෙකු ගමන් කරනා විට අඩු වේගයකින් ද ගමන් කර බවයි.
ζ = Iα සම්බන්ධය ලබා ගැනීම
- වස්තුවක් මත කෝණික ගම්යතාවය වෙනස් වීමේ සීඝ්රතාවය එම වස්තුව මත ක්රියා කරන බාහිර ව්යාවර්තය ට අනුලෝමව සමානුපාතික වන අතර කෝණික ගම්යතාවය වෙනස් වන අක්ෂය ඔස්සේ ව්යාවර්තයේ දිශාව පිහිටයි.
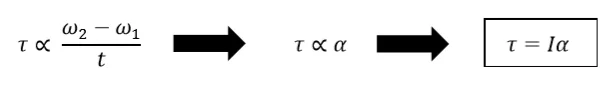
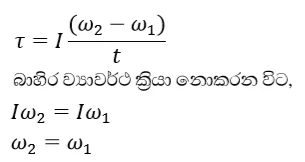
භ්රමණ කාර්යය
- යම් වස්තුවක් මත යම් අක්ෂයක් වටා ව්යාවර්තයක් යෙදීම නිසා එම අක්ෂය වටා කෝණික විස්ථාපනයක් ඇතිවීමෙන් භ්රමණ කාර්යයක් සිදු වේ.
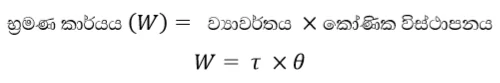
භ්රමණ ක්ෂමතාව
- භ්රමණ කාර්යය කිරීමේ ශීඝ්රතාවය , භ්රමණ ක්ෂමතාවය නම් වේ.
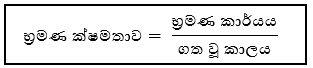
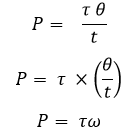
භ්රමණ චාලක ශක්තිය
- භ්රමණය වන වස්තුවක කාර්යය කිරීමේ හැකියාව එම වස්තුවේ භ්රමණ චාලක ශක්තිය නම් වේ.
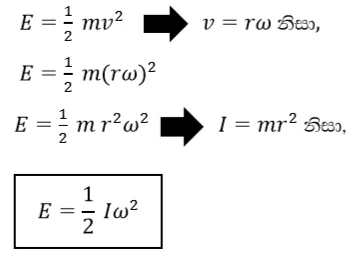
භ්රමණ චලිතය සඳහා කාර්යය – ශක්තිය මූලධර්මය
- කිසියම් වස්තුවක් මත යම් අක්ෂයක් වටා යෙදෙන ව්යාවර්තය මගින් කෙරෙන කාර්යය ප්රමාණය එම අක්ෂය වටා සිදු වූ භ්රමණ චාලක ශක්ති වෙනස්වීමට සමාන වේ.



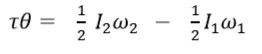



පෙරලුම් චලිතය
වස්තුවක රේඛීය චලිතයක හා භ්රමණ චලිතයක එකතුවක් ලෙස වස්තුවක පෙරළීම සිදු වේ.
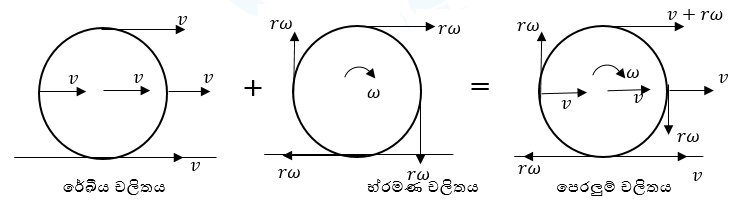
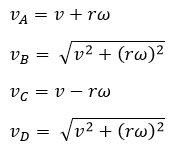
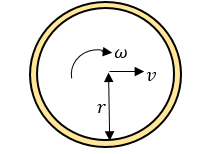
- ලිස්සීමකින් තොරව පෙරලෙන විට රේඛීය චලිතයෙන් ලැබෙන ප්රවේගය භ්රමණ චලිතයේ ස්පර්ශීය ප්රවේගයට සමාන වේ. එම නිසා වේ.
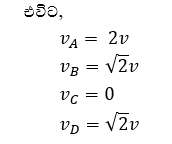
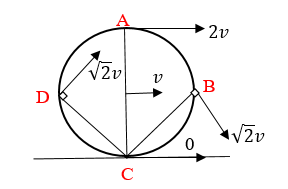

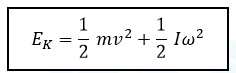
උදා :-
- ස්කන්ධය m වන වළල්ලක් v ප්රවේගයෙන් පෙරළීගෙන යන විට එහි මුලු චාලක ශක්තිය m හා v ඇසුරින් සොයන්න.
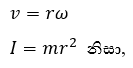
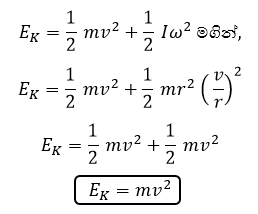
රේඛීය චලිතය හා භ්රමණ චලිතය අතර අනුරූපතාව

ඉදිරියේදී ප්රශ්න ඇතුලත් වන්නේ මෙතනටයි.



