මාන හැඳින්වීම
- කිසියම් භෞතික රාශියක් මූලික භෞතික රාශියක් සමඟ බැඳී පවතින ආකාරය දක්වන ප්රකාශනයට එම භෞතික රාශියේ මාන දැක්වීම යැයි කියයි.
- යාන්ත්ර විද්යාවේදී භාවිත වන මූලික භෞතික රාශි 3කි.
| භෞතික රාශිය | මාන |
| ස්කන්ධය | M |
| දිග | L |
| කාලය | T |
ව්යුත්පන්න භෞතික රාශිවල මාන
මාන උපයෝගී කරගෙන ව්යුත්පන්න භෞතික රාශීන්ගේ මාන ලබා ගන්න ආකාරය පහත දැක්වේ.
පූර්ණ වශයෙන් මාන සහිත භෞතික රාශි
| භෞතික රාශිය | ලැබෙන ආකාරය | මාන |
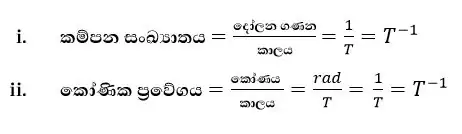
| වේගය | දුර/කාලය | L T-1 |
| ප්රවේගය | විස්ථාපනය/කාලය | L T-1 |
| ත්වරණය | ප්රවේග වෙනස/කාලය | L T-2 |
| බලය | ස්කන්ධය × ත්වරණය | M L T-2 |
| කාර්යය | බලය × විස්ථාපනය | M L2 T-2 |
| ශක්තිය | කරන ලද කාර්යය ප්රමාණය | M L2 T-2 |
| ක්ෂමතාව | කාර්යය/කාලය | M L2 T-3 |
| වර්ගඵලය | දිග × පළල | L2 |
| පරිමාව | දිග × පළල × උස | L3 |
| පීඩනය | අභිලම්භ බලය/වර්ගඵලය | M L-1 T-2 |
| ඝනත්වය | ස්කන්ධය/පරිමාව | M L-3 |
අර්ධ වශයෙන් මාන ඇති භෞතික රාශි
මාන රහිත භෞතික රාශි

මාන වල ලාක්ෂණික
- භෞතික රාශියේ මාන දැක්වීම මඟින් එම භෞතික රාශියේ විශාලත්වය නිරූපනය නොකෙරේ.
- එම නිසා භෞතික රාශියේ විශාලත්වය කුමක් වුවත් එහි එහි මාන එකම වේ.
- භෞතික රාශියක මාන මඟින් ඒකක ක්රමය නිරූපනය නොකෙරේ.
- ඕනෑම ඒකක ක්රමයකින් භෞතික රාශියක මාන එකම වේ.
- භෞතික රාශීන් දෙකක මාන සමාන වීමෙන් එම භෞතික රාශීන් සමාන වන බව නොදක්වයි.
උදා:
- කාර්යය හා බල ඝූර්ණය
- සංඛ්යාතය හා කෝණික ප්රවේගය
මෙම රාශීන්යුගල වල මාන සමාන වුවද එම රාශි සමාන නොවේ.
- භෞතික රාශි දෙකක් සමාන කල හැක්කේ , එකතු කල හැක්කේ ,අඩු කල හැක්කේ ඒවයේ මාන සමාන නම් පමණි.
- භෞතික රාශීන් කිහිපයක ගුණාකාරයක් සහිත පද කිහිපයක් සමාන කල හැක්කේ , එකතු කල හැක්කේ, අඩු කල හැක්කේ ඒවායේ මාන සමාන නම් පමණි.
- පද කිහිපයක එකතුවකට හෝ අන්තරයකට පවතින්නේ එක් පදයක මාන වේ.
- මාන සහිත පදයකට හෝ පද කිහිපයකට මාන නොමැති නියත පද යක් එකතු කල නොහැක.
- මාන සහිත සියලු ම රාශීන්ට ඒකකයක් පවතී.
- ඒකක පවතින සමහර රාශීන්ට මාන නොමැත.
උදා:
- තල කෝණය
- ඝන කෝණය
මාන විශ්ලේෂණයේ භාවිත
- සමීකරණය නිවැරදි දැයි සොයා බැලිය හැකිය.
- දී ඇති රාශියක ඒකක හා මාන සෙවීම.
- සමීකරණ ගොඩ නැගිය හැකිය.
- එක් ඒකක ක්රමයක් තවත් ඒකක ක්රමයකට පරිවර්තනය කල හැකිය.
සමීකරණය නිවැරදි දැයි පරීක්ෂා කිරීම
- භෞතික විද්යාවේ පද කීපයක් සහිත සමීකරණයක සෑම පදයකට ම සමාන මාන තිබිය යුතුයි.
උදා:
- S=ut+\frac12at^2\; මෙහි S විස්ථාපනය,u ආරම්භක ප්රවේගය,t කාලය ,a ත්වරණය ඉහත සමීකරණයේ සෑම පදයක ම සමාන මාන ඇති බව පෙන්වන්න.
[S] =L
[ut] =LT-1 x T x L=L
[at2]=LT-2 x T2=L
[S] = ut හි මාන=at2 හි මාන
- V2=U2+2aS සමීකරණයේ S විස්ථාපනය, U ආරම්භක ප්රවේගය, V අවසාන ප්රවේගය, a ත්වරණය ඉහත සමීකරණයේ සෑම පදයක ම සමාන මාන ඇති බව පෙන්වන්න.
[V2]= (L T-1)2 =L2 T-2
[U2]= (L T-1)2 =L2 T-2
[aS]= LT-2 x L =L2 T-2
[V2]= [U2]= [aS]
- P+\frac12\rho V^2+\rho gh=K සමීකරණයේ P පීඩනය, V ප්රවේගය, ρ ඝනත්වය, g ගුරුත්වජ ත්වරණය, h උස නම්,
- ඉහත සමීකරණයේ සෑම පදයක ම සමාන මාන ඇති බව පෙන්වන්න.
- K හි මාන සොයන්න.
[P] = M L-1 T-2
[ρV2] = (M L-3) x (L T-1)2 = M L-1 T-2
[ρgh] = (M L-3) x (L T-2) x (L) = M L-1 T-2
[P] = [ρV2] = [ρgh]
[K] = [P] = M L-1 T-2
දී ඇති රාශියක ඒකක හා මාන සෙවීම
උදා:
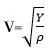
- ඉහත සමීකරණයේ v යනු ඝන මාධ්ය තුල ධ්වනි ප්රවේගය, ρ ඝනත්වය Y යංමාපාංකය නම්, Y හි ඒකක හා මාන මොනවාද?
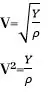
Y=V2ρ
=(LT-1)2(ML-3)
=(M)(L)-1(T)-2
=kg m-1 s-2
- V=\frac{K_1}{t+K_2}+K_3\;t^2 ඉහත සමීකරණයේ V ප්රවේගය, t කාලය නම්, K1,K2,K3 හි මාන සොයන්න.
[V]= [K3t2]
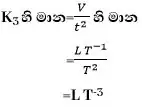
[T] =[K2]
[K2] =[T]
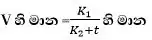
[V] = \left[\frac{K_1}{t+K_2}\right]
[K1]=[V] \times [K2+t]
=LT-1 \times T
=L
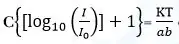
මෙහි I හා I0 යනු විද්යුත් ධාරාවන් ය. C යනු නියතයක් නම්,


මාන විශ්ලේෂණය මඟින් ප්රකාශන ව්යුත්පන්න කිරීම
- පහත සඳහන් අවස්ථාවල දී කිසියම් භෞතික රාශියක් තවත් භෞතික රාශීන් කීපයක් සමඟ බැඳී ඇති විට ඒවා අතර සම්බන්ධය ගොඩනගා ගැනීමට මාන විශ්ලේෂණය යොදා ගත හැකිය.
- භෞතික රාශිය තවත් භෞතික රාශි 3 ක් හෝ ඊට අඩු ප්රමාණයක් සම්බන්ධ වී තිබිය යුතුයි.
- එකම මාන සහිත භෞතික රාශීන් 2 ක් සමඟ බැඳී නොතිබිය යුතුයි.
- මාන නොමැති භෞතික රාශියක් සමඟ බැඳී නොතිබිය යුතුයි.
- පද කීපයක එකතුවක් නොතිබිය යුතුයි.
- පළමුවෙන්ම පරීක්ෂණාත්මක ලෙස කිසියම් භෞතික රාශියක් තවත් කුමන රාශීන් සමඟ බැඳී ඇති දැයි හඳුනා ගත යුතුයි.
- ඉන්පසුව පහත පියවර අනුගමනය කරන්න.
උදා:
- සරල අවලම්භයක ආවර්ත කාලය T එහි දිග L හා ගුරුත්වජ ත්වරණය g මත රඳා පවතින බව පරීක්ෂණාත්මක ව සොයා ගෙන ඇත. මාන විශ්ලේෂණය මඟින් ආවර්ත කාලය සඳහා ප්රකාශයක් ලබා ගන්න.
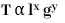
T = K lx gy (K යනු සමානුපාතික නියතයකි.)
මාන ආදේශයෙන්,
T = K [L]x [LT-2]y
T = K [L](x+y) [T]-2y
T හි මාන සලකමු. 1= -2y
L හි මාන සලකමු. 0=x+y
y=-1/2 , x=1/2
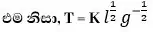
පරීක්ෂණාත්මක ව K = 2π බව සොයා ගෙන ඇත.
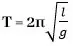
- වෘත්තාකාර පථයක ගමන් කරන වස්තුවක් මත කේන්ද්ර අභිසාරී බලය F, වස්තුවේ ප්රවේගය V, ස්කන්ධය m, වෘත්තයේ අරය r මත රඳා පවතී. මාන විශ්ලේෂණයෙන් කේන්ද්ර අභිසාරී බලය සඳහා ප්රකාශනයක් ගන්න.
F α Vx my rz
F = K Vx my rz (K යනු සමානුපාතික නියතයකි.)
මාන ආදේශයෙන්,
F = K [LT-1]x [M]y [L]z
F = K [L](x+z) [M]y [T]–x
T හි මාන සලකමු.
-2 = -x
x= 2
M හි මාන සලකමු.
y= 1
L හි මාන සලකමු.
x+z= 1
විසදීමෙන්, z= -1
අගයයන් ආදේශයෙන්,
F = K V2 m1 r-1
F = K
K = 1 බව පරීක්ෂණාත්මක ව සොයා ගෙන ඇත.
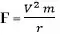
එක් ඒකක ක්රමයක් තවත් එකක ක්රමයකට පරිවර්තනය කිරීම
- පළමුවෙන් දී ඇති භෞතික රාශියේ මාන ලබා ගන්න.
- මුලික රාශි පරිවර්තනය කිරීමට අවශ්ය ගුණන සාධකය ලියා එමගින් ගුණ කල යුතූ හෙවත් ගුණන සාධකය ගණනය කරන්න.
උදා:
- 25 mm2 ,m2 කරන්න.
වර්ගඵලයේ මාන=[L]2
ගුණන සාධකය =(10-3)2
=10-6
- 25 mm2 =25×10-6 m2
- 20 cm ms-1 , m s-1 කරන්න.
ප්රවේගයේ මාන=[L][T]-1
=(10-2)x(10-3)-1
=10
20 cm ms-1 =200 m s-1
- 0.00035 m2 වර්ගඵලය cm2 වලින් දක්වන්න.
වර්ගඵලයේ මාන=[L]2
ගුණන සාධකය =(102)2
=104
0.00035 m2 =0.00035 x 104 cm2
=3.5 cm2
- 35 mm3 පරිමාණ m3 වලින් ලියන්න.
පරිමාවේ මාන=L3
ගුණන සාධකය=(10-3)3
=10-9
35 mm3 =35×10-9 m3
- 30 m s-1 ප්රවේගය km h-1 වලින් දක්වන්න.
වේගයේ මාන=[L][T]-1
ගුණන සාධකය=(10-3)x(3600-1)-1
=3600/1000
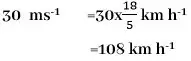
- ස්කන්ධ g වලින් දුර cm වලින් කාලය ms වලින්ද ගත් විට බලය 0.25 g cm ms-2 ලෙස ලැබේ. එම බලය N වලින් දක්වන්න.
බලයේ මාන=M L-1 T-2
ගුණන සාධකය=(10-3) x (10-2) x (10-3)-2
=10
0.25 g cm ms-2=0.25×10 N
=2.5 N
- දුර cm වලින්ද ස්කන්ධය g වලින්ද කාලය s වලින්ද ගත් විට පීඩනය 2.5×105 g cm-1 s-2 ලෙස ලැබේ. මෙම පීඩනය Pa වලින් ප්රකාශ කරන්න.
පීඩනයේ මාන=M L-1 T-2
=(10-3) x (10-2)-1
=10-3x102
=10-1
2.5×105 g cm-1 s-2=2.5×105x10-1 Pa
=2.5×104 Pa
මාන විශ්ලේෂණයේ සීමාවන්
- සමීකරණයක තිබිය හැකි මාන රහිත නියතක අගය සෙවිය නොහැකිය.
උදා:
\text{S=ut+}\frac{\text{1}}2\text{at}^2\text{ සමීකරණයේ }\frac12\text{ යන නියතය මාන විශ්ලේෂ්ණයෙන් සෙවිය නොහැක.}- සමීකරණයක් තේරුමක් සහිත සාධාරණ සමීකරණයක් වීමට තිබිය යුතු අමතර පද තිබිය යුතු දැයි තීරණය කල නොහැක.
උදා: s=ut+1/2at2සමීකරණ්යේ ut පදය නොමැති වුවත් සමීකරය මාන අතින් නිරවද්ය වේ. නමුත්,S=ut+1/2at2 සමීකරණය (සැමවිටම) සත්ය නොවේ.
- එකම මාන ඇති වෙනස් භෞතික රාශීන් වෙන වෙනම හඳුනා ගත නොහැක.
උදා: කාර්යයට හා බලඝූර්ණයට සමාන මාන තිබුනද ඒවා සම්පූර්ණයෙන් ම වෙනස් භෞතික රාශීන් දෙකකි.
- මාන විශ්ලේශනය මඟින් ව්යුත්පන්න කල හැකි වනුයේ භෞතික රාශීන් තුනක් හෝ තුනකට අඩු සංඛ්යාවක් පමණක් ඇති සමීකරණයි. නැතහොත්, සමීකරණ සංඛ්යාවට වඩා විචල්යයන් සංඛ්යාව වැඩි වන නිසා අදාල සමීකරණය ගොඩ නැගිය නොහැකිය.
- කිසියම් රාශියකට හෝ රාශි සංයෝජනයකට මාන නොපවතී නම් පමණක් සංඛ්යාවක හෝ කිසියම් රාශියක හෝ ඝාතීය ශ්රිතයේ හෝ දර්ශකයක් ලෙස යොදා ගත හැක.
උදා: 10x, Ax, ℮x
මෙහි x රාශියට මාන නොතිබිය යුතුය.
- කිසියම් රාශියකට හෝ රාශි සංයෝජනයකට හෝ මාන නොපවතී නම් පමණක් එහි ලඝුගණකය පිලිබඳ සලකා බලයි.
එනම්, ලඝුගණක ගැන සලකා බැලිය හැකි වනුයේ සංඛ්යාවල පමණි.
උදා:
\log\left(x\right)මෙහි x රාශියට මාන නොමැති විය යුතුයි.
Video link:
Results
#1. N=No e-λ tසමීකරණයේ N හා No යනු පරමාණුක න්යෂ්ටි සංඛ්යාවන් වන අතර t යනු කාලයයි. 𝞴හි මාන සමාන වන්නේ,
#2. ඇදි තන්තුවක ස්ථාවර තරංග සංඛ්යාතය f=P/2l √(T/m) සමීකරණය මගින් ලබා දෙයි. මෙහි T යනු ආතතිය ද, l - තන්තුවේ දිග ද, P - පුඩු ගණන ද නිරූපණය කරයි නම් m හි මාන වන්නේ,
#3. පීඩනය පරිමාවෙන් ගුණ කිරීමෙන් ලැබෙන රාශියේ මාන වලට සමාන වන්නේ පහත සඳහන් කුමන රාශියක මාන ද?
#4. පහත සඳහන් ඒවායින් SI ඒකකයක් නො වන්නේ,
#5. දී ඇති A, B, C අවස්ථා තුනෙන් ඒකක නිවැරදිව ලියා ඇති අවස්ථාව/අවස්ථා වන්නේ,
A. mm s-1
B. mm/s
C. mm. s-1
#6. පහත ඒවායින් මාන නොමැති රාශිය/රාශීන් වන්නේ, a. සාපේක්ෂ ඝනත්වය b. සාපේක්ෂ ප්රවේගය c. ඝර්ෂණ සංගුණකය
#7. වාහනයක් ගමන් කල දුර S හා ගත වූ කාලය t අතර සම්බන්ධය දක්වන සමීකරණය S= At2 (1 + 1/2 Bt) වේ. මෙහි A හා B වල මාන පිළිවෙළින්,
#8. ප්රධාන පරිමාණයේ මිලි මීටර කොටස් 24 සමාන කොටස් 25 ට බෙදීමෙන් සාදා ඇති වර්නියර් පරිමාණයකින් පැත්තක දිග 12mm වන ඝනකයක පැති මැන එහි පරිමාව ගණනය කිරීමේ දී සිදු වන ප්රතිශත දෝශය වන්නේ, (ගුණ කිරීමේ දී භාගික දෝෂය එකතු වේ.)
#9. පරීක්ෂකයා මත රඳා පවතින දෝෂය වන්නේ,
#10. මීටර් රූල භාවිතයෙන් ලබාගත් අගයක් 40.0 cm ලෙස වුවත් පසුව එහි පරිමාණය වැරදි ලෙස සලකුණු කර ඇති බව සොයා ගන්නා ලදී. එහි සත්යය අගය 39.7 cm වුණි නම් සිදුවී ඇති දෝෂය,
#11. ඇදි තන්තුවක් ඔස්සේ තීර්යක් තරංග වේගය v පහත සමීකරණය ලබා දෙයි. v=CTxmy+ 1/2 kT2 වේ. T යනු තන්තුවේ ආතතිය ද m යනු ඒකක දිගක ස්කන්ධය ද වේ. C යනු මාන රහිත නියතයක් වන අතර k යනු මාන සහිත නියතයකි. x හා y හි අගයන් වන්නේ,
#12. මේ අතරින් දෛශික රාශිය කුමක්ද ?
#13. පහත ඒවායින් අදිශ රාශියක් වන්නේ ,



