ප්රිස්මයක අවම අපගමන අවස්ථාව සෙවීම
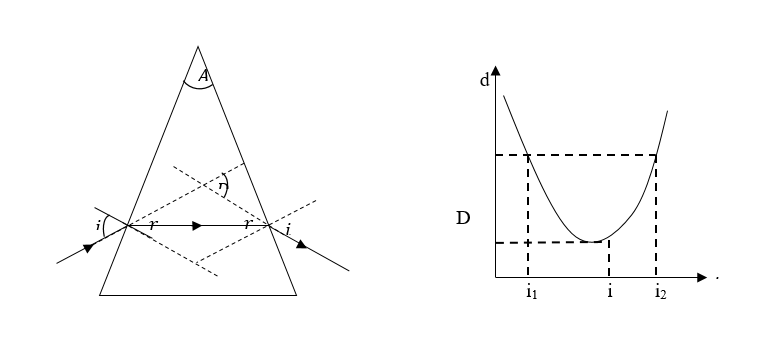
- ප්රිස්මයක් මත පතනය වන ආලෝක කිරණයක මුල් පතන කෝණය ක්රමයෙන් වැඩි කරමින් කිරණයේ අපගමන කෝණය සොයා පතන කෝණය ඉදිරියෙන් ප්රස්තාර ගත කළවිට රූපයේ පරිදි ප්රස්තාරයක් ලැබේ.
- එනම් පතන කෝණය ක්රමයෙන් වැඩිකරන විට අපගමන කෝණය ක්රමයෙන් අඩුවී අවම අගයකට පැමිණ නැවතත් ක්රමයෙන් වැඩි වේ.
- අපගමන කෝණය ලබාගන්නා මෙම අවම අගය අවම අපගමන කෝණය (D) වශයෙන් හඳුන්වයි.
- අපගමන කෝණය වෙනත් d අගයකදී ඊට අනුරූපව පතන කෝණ දෙකක් (i1 සහ i2) ඇති බව ප්රස්තාරයෙන් පෙනේ.
- ආලෝකයේ ප්රතිවර්ත්යතාව සැලකූ විට එම i1 සහ i2 කෝණ ප්රිස්ම සටහනේ සලකුණු කර ඇති මුල් පතන කෝණය හා දෙවන මුහුණතින් නිර්ගත කෝණය වන බව පෙනේ.
- මේ අනුව ප්රිස්මයක් හරහා ගමන් කරන කිරණයක් සඳහා එකම අපගමන කෝණයක් ඇති පතන කෝණ දෙකක් ඇති බව පෙනේ.
- අවම අපගමන අවස්ථාවේදි එම i1 සහ i2 කෝණ දෙකම එකම i අගයක් ගන්නා බව පැහැදිළිය. වර්තන නියම වලට අනුව මෙම අවම අපගමන අවස්ථාවේදි ඉහත ප්රිස්ම සටහනේ r1 සහ r2 කෝණද සමාන වියයුතුය.
- එනම් අවම අපගමන අවස්ථාවේදි වර්තිත කිරණය ප්රිස්මය හරහා සමමිතිකව ගමන් කරයි.
අවම අපගමන අවස්ථාව සඳහා වර්තන අංක වල සම්බන්ධය
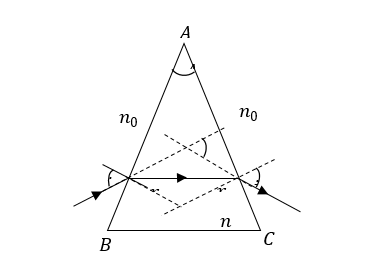
- වර්තන අංකය no වන විරල මාධ්යයක තබා ඇති වර්තන කෝණය A වන වර්තන අංකය n වූ ප්රිස්මයක් හරහා D අවම අපගමන කෝණයක් යටතේ ආලෝක කිරණයක් ගමන් ගන්නා අවස්ථාව සලකමු.
- I මුහුණතේ වර්තනයට ස්නෙල් නියමය යොදමු.
noSini = nSinr
n / no = Sini / Sinr …………… (1)
ඉහත සටහනට අනුව, r + r = A
r = A / 2
තවද i – r + i – r = D
2i – 2r = D
2i – A = D
i = (A + D) / 2
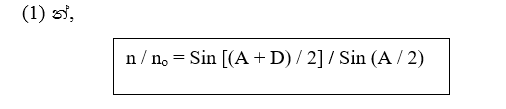
අවට විරල මාධ්යයට වාතය හෝ රික්තය ඇත්නම් no = 1 වේ.
එම නිසා,
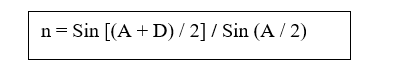
(විරල මාධ්යය වෙතට ගහන මාධ්යයකින් කිරණ ගමන් කරනවිට)
ප්රිස්මයක අවම අපගමන කෝණය සෙවීම
- අඳින පුවරුව මත සුදු කඩදාසියක් තබන්න.
- එම කඩදාසිය මත ප්රිස්මය තබා එහි මායිම පැන්සලකින් ලකුණු කරන්න.
- ප්රිස්මයේ එක් පාදයක් මත දන්නා පතන කෝණයක් සහිත රේඛාවක් අඳින්න. එම රේඛාව මත ප්රිස්මයට ආසන්නව P ඇල්පෙනෙත්තද, ටිකක් ඈතින් Q ද සිටවන්න.
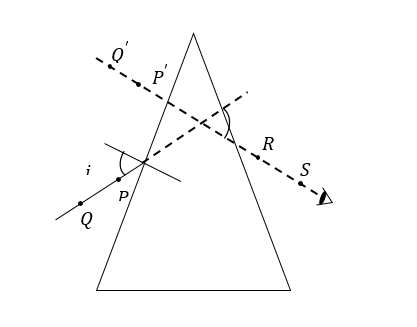
- නිර්ගත මුහුණතින් බලා P හා Q ඇල්පෙනෙතිවල නිර්ගත ප්රතිබිම්භ වන P/ හා Q/ සමඟ ඒකරේඛීය වන සේ R හා Q ඇල්පෙනෙති එකිනෙකට මඳක් ඈතින් සිටවන්න.
- දැන් ප්රිස්මය ඉවත්කර, අදාළ රේඛා දික්කර අපගමන කෝණය D සොයාගන්න.
- ඉන්පසු I වැඩිකරමින් ඉහත පරිදි පරීක්ෂණයෙන් D ලබාගන්න.
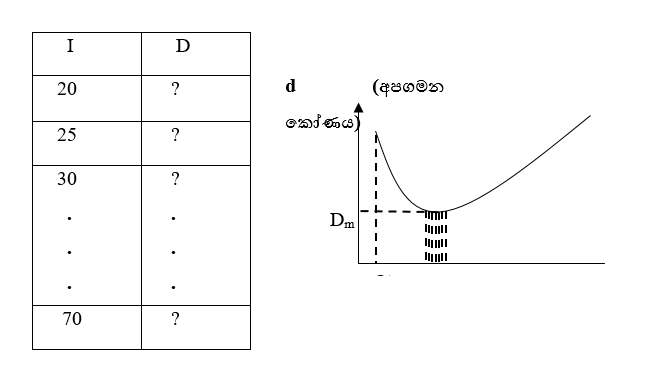
- ප්රස්තාරය මගින් අප සොයගන්නා වැදගත්ම අගය Dm වේ. එම Dm ඉතා නිවැරදිව ගැනීම සඳහා පහත පරීක්ෂණාත්මක ක්රමය අනුගමනය කරන්න.
- අවම අපගමනය ලැබෙන පතන කෝණය දෙපසින් තවත් ඉතා ආසන්න පතන කෝණ කිහිපයකට එම පරීක්ෂණය නැවතත් සිදු කර අපගමන කෝණ ලබාගන්න.
- කිරණය නිර්මාණය සඳහා අවශ්ය ඇල්පෙනෙති දෙක එකිනෙකට ඈතින් සිටවනු ලබයි. එවිට ඒවා යා කිරීමෙන් නිවැරදි රේඛා එකක් පමණක් ලැබේ. ඒවා ළඟින් සිටවූයේ නම් රේඛා කිහිපයක් ලැබිය හැක.
- ඇල්පෙනෙති සිරස්ව සිටවිය යුතුය. නැතහොත් ප්රතිබිම්භය ඇද වේ.
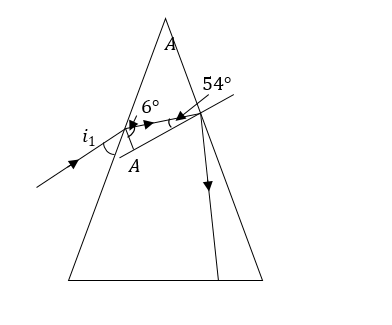
- මෙම පරීක්ෂණය ආරම්භයේදී පතන කෝණයට 200 ට වඩා අඩු අගයයන් තබාගැනීම සුදුසු නැත. මෙවිට i1 කුඩා නිසා r1 ද කුඩා වේ. මෙවිට r2 > C වන බැවින් කිරණය පූර්ණ අභ්යන්තර පරාවර්තනයට ලක්වේ. ඒ අනුව ප්රතිබිම්භයක් දැකගත නොහැකි වේ.
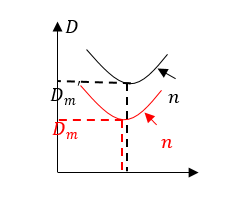
- ප්රිස්මයේ වර්තනාංකය විශාල නම් අවම අපගමන කෝණය සඳහා ඇත්තේද විශාල අගයකි.
↑ n = Sin [A + ↑ (Dm / 2)] / Sin (A / 2) (A නියත වේ.)
අවධි කෝණ ප්රමේයය භාවිතයෙන් ප්රිස්මයක වර්තනාංකය සෙවීම
- සුදු කඩදාසියක් මත ප්රිස්මය තබා එහි මායිම ලකුණු කරන්න.
- ප්රිස්මයේ x – z සමඟ ස්පර්ශ වන සේ, මැදට මඳක් ඉහළින් P ඇල්පෙනෙත්ත සිටවන්න.
- y – z තුළින් xy දෙස බලමින් y සිට z දක්වා ඇස ගෙනයන්න.
- P වල ප්රතිබිම්භය පෙනෙන – නොපෙනෙන අවස්තාවට අනුරූපව ප්රතිබිම්භය සමඟ ඒකරේඛීය වන සේ Q හා R ඇල්පෙනෙති සිටවන්න.
නිර්මාණ
- RQ යා කර, එම රේඛාව y – z පාදය හමුවන ලක්ෂ්ය S ලෙස ගන්න.
- P වල සිට x – y ට ලම්භකයක් ඇඳ, PT = TU වන තෙක් එය දික් කරන්න.
- U හා S යා කරන්න. එම රේඛාව xy හමුවන ලක්ෂ්ය W වේ. PW යා කරන්න.
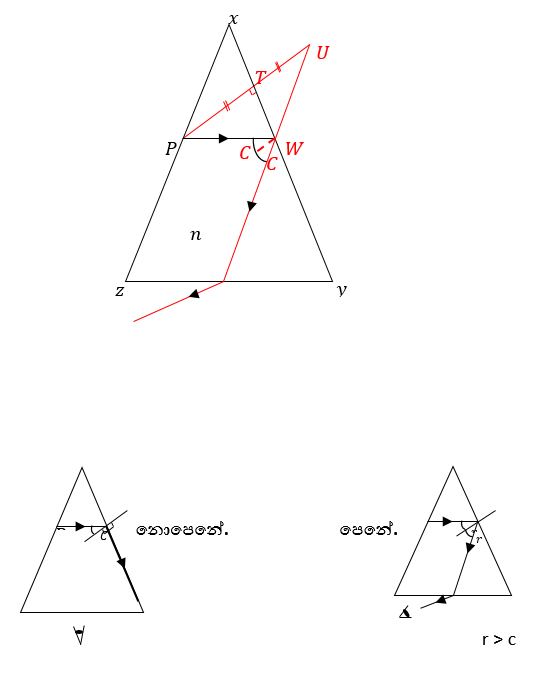
අවධි කෝණ ක්රමය භාවිතයෙන් ද්රවයක වර්තනාංකය සෙවීම
- ප්රිස්මයේ xy පාදය සමඟ ස්පර්ශවන සේ ජලය තැවරූ අන්වීක්ෂ කදාවක් තබා, එම පරීක්ෂණය එලෙසම සිදුකර 2C1 කෝණය ලබාගන්න.
- පහත පරිදි ගණනයෙන් ද්රවයේ වර්තනාංකය nw ලබාගත හැක.
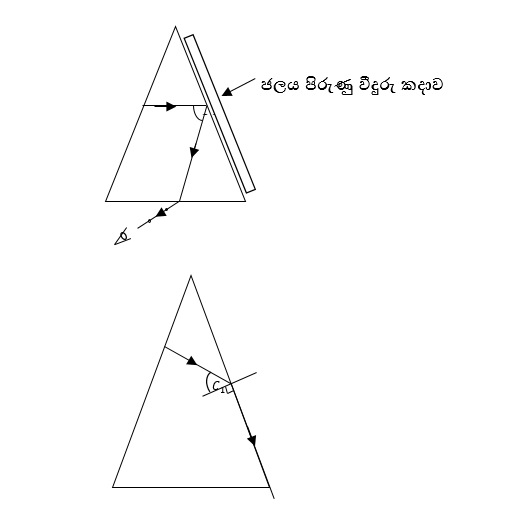
ngSinC1 = nwSin900
ngSinC1 = nw
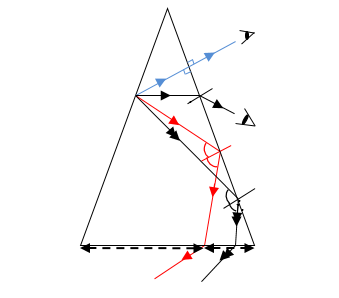
මෙම පරීක්ෂණයේදී P ඇල්පෙනෙත්ත xy පාදය සමඟ ස්පර්ශ වන සේ සිටුවා ඇත්තේ ආලෝක කිරණ xy පාදයෙන් වර්තනය වීම වැළැක්වීමටයි.
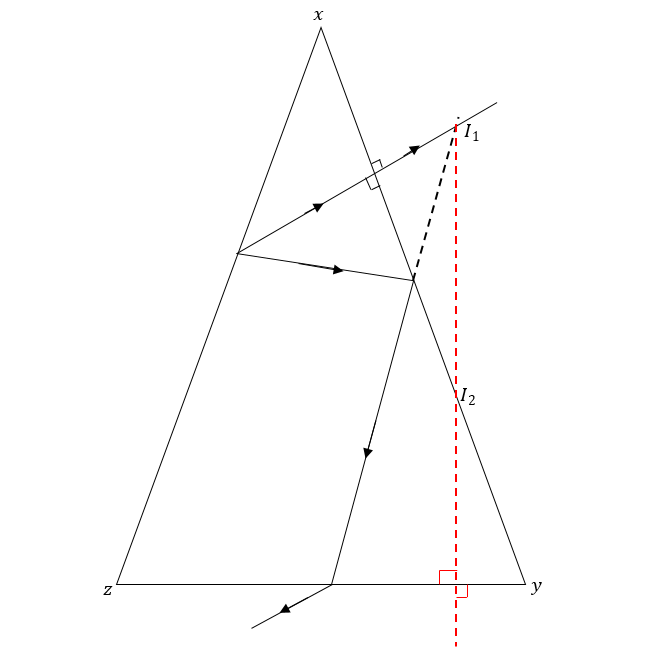
- xy පෘෂ්ඨයෙන් සාදන P වස්තුවේ ප්රතිබිම්භය වන I1, yz පෘෂ්ඨය සඳහා අතාත්වික වස්තුවක් ලෙස ක්රියා කරයි.



