රේඛීය චලිතය
නියම දිශාවක් ඔස්සේ හෙවත් සරල රේඛීය පථයක් දිගේ සිදුවන චලිතය “රේඛීය චලිතය” නම්වේ.
දුර හා විස්ථාපනය
- චලිත වන වස්තුවක පිහිටීමේ සිදුවන වෙනස්වීම “දුර” ලෙස හැඳින්වේ. මෙය වස්තුව ගමන් කරන මාර්ගය මත රඳා පවතී.
- උදාහරණයක් ලෙස A හා B නම් නගර දෙකක් සලකමු. පහත රූපයට අනුව A නගරයේ B නගරය කරා යාමට හැකි මාර්ග කිහිපයක් ඇතැයි සිතමු. එවිට, මේ එක් එක් මාර්ගය ඔස්සේ ගෙවා යා යුතු දුරවල් එකිනෙකට වෙනස් බව පැහැදිලිය.
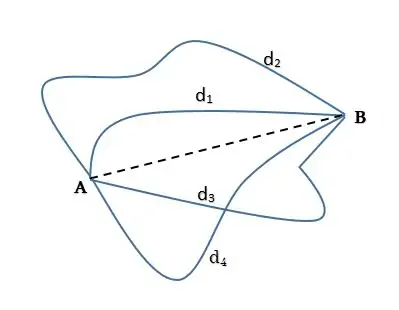
- වස්තුවක චලිතයේ ආරම්භක ලක්ෂ්යයත් අවසාන ලක්ෂ්යයත් අතර ගමන් මඟේ දිග, වස්තුව ගමන් කළ දුර ලෙස හඳුන්වයි.
- වස්තුවට A සිට B දක්වා මාර්ග කිහිපයක් ඔස්සේ ගමන් කළ හැකිය. මාර්ගය අනුව ගමන් කරන දුර වෙනස් ය.
- දුර අදිශ රාශියකි. එයට ඇත්තේ විශාලත්වයක් පමණි.
- ඉහත රූපයේ දැක්වෙන A නගරයේ සිට B නගරය දක්වා කෙටිම දුරක් සහිත ගමන් මඟ AB යාකරන රේඛාව දැක්වෙන කඩ ඉර මඟින් ලැබේ.
- මේ අනුව ලක්ෂ්යය දෙකක් අතර තිබිය හැකි කෙටිම දුර එම ලක්ෂ්යය දෙක අතර “විස්ථාපනය” ලෙස හැඳින්වේ.
- විස්තාපනය දෛශික රාශියකි. එයට විශාලත්වයක් මෙන්ම දිශාවක්ද ඇත.
- දුර සහ විස්තාපනය මැනීමේ SI ඒකකය m (මීටර්) වේ.
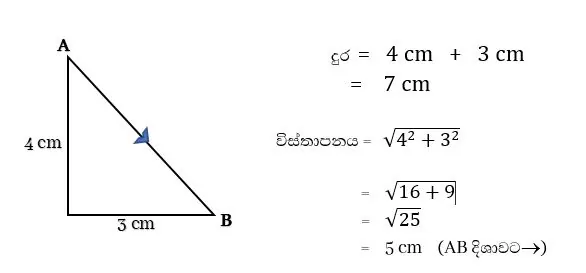
උදාහරණ :- A සිට B දක්වා දුර සහ විස්තාපනය සොයමු.
වේගය
- චලනය වන වස්තුවක පිහිටීම වෙනස් වීමේ සීඝ්රතාව, එනම් ඒකක කාලයකට ගමන් කරන දුර එහි වේගය වේ.
- වේගය අදීශ රාශියකි. වේගයට ඇත්තේ දිශාවක් පමණි. වස්තුවක් සමාන කාලාන්තර වලදී සමාන දුර ප්රමාණ ගමන් කරයි නම්, එය නියත වේගයෙන් ගමන් කරන්නේ යැයි කියනු ලැබේ.
උදාහරණ :-
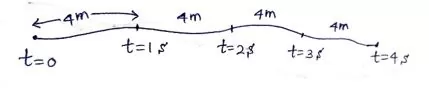
- එසේ නොවන අවස්තාවලදී වස්තුවේ වේගය වෙනස් වන බැවින් එහි චලිතය සඳහා සාමාන්ය වේගයක් පමණක් ප්රකාශ කෙරේ.
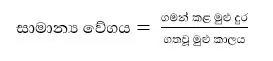
උදාහරණ :-


- සාමාන්ය වේගයේ ඒකක m s-1 හෝ km h-1 වේ.
උදාහරණ 1 :- බස් රථයක් A නම් නගරයක සිට B නම් නගරයක් දක්වා යාමට පැය 3ක කාලයක් ගනී. නගර දෙක අතර දුර 72 km වේ. බස් රථයේ සාමාන්ය වේගය සොයන්න.
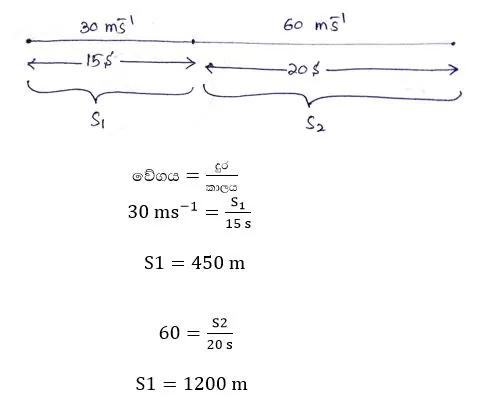
එමනිසා ගමන් කළ මුළු දුර = S1 + S2 = 1650 m
ගතවූ මුළු කාලය = 20 s + 15 s = 35 s

ප්රවේගය
- චලනය වන වස්තුවක විස්ථාපනය වෙනස් වීමේ ශීඝ්රතාව, “ප්රවේගය” නම් වේ.
- එනම් ඒකක කාලයකදී සිදු කරන ලද විස්ථාපනයයි.
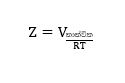
- විස්ථාපනය දෛශිකයක් බවින් ප්රවේගයද දෛශිකයකි. එනම් ප්රවේගයට විශාලත්වයක් මෙන්ම දිශාවක්ද ඇත.
- ප්රවේගයේ ඒකකයද m s-1 හෝ km h-1 වේ.
- තවද යම් වස්තුවක් t කාලයක් තුළදී S නම් විස්ථාපනයක් ඇති කරයි නම් එම වස්තුවේ ප්රවේගය සෙවීමට,
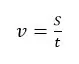
සමීකරණය යොදාගත හැකිය.
නියත වේගයෙන් වෘත්ත චලිතයක් සිදු කරන අංශුවක් සලකන්න.
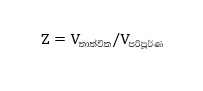
- අංශුවේ වේගය නියත වුවද චලිත දිශාව සෑම මොහොතකම වෙනස් ය. එබැවින් මෙය නියත වේගයෙන්, එනමුත් වෙනස් වන ප්රවේගයෙන් ගමන් කරන අංශුවකට හොඳ උදාහරණයකි.
- මේ අනුව ඒකාකාර ප්රවේගයෙන් ගමන් කිරීමට නම් වේගය මෙන්ම දිශාවද නොවෙනස් විය යුතුය.
- එබැවින් ඒකාකාර ප්රවේගයක් තිබිය හැක්කේ රේඛීය චලිතයක් සිදු කරන වස්තුවකට පමණි.
- රේඛීය චලිතයක් සිදු කරන වස්තුවක්, සමාන කාලාන්තර වලදී සමාන විස්ථාපන සිදු කරයි නම්, එය ඒකාකාර ප්රවේගයෙන් චලිත වේ යැයි කියයි.
උදාහරණ 1 :- වස්තුවක් සරල රේඛීය මාර්ගයක් ඔස්සේ A සිට B දක්වා 40 m දුරක විස්ථාපනයක් සිදුකරයි. ඒ සඳහා ගතවූ කාලය 10 s නම්, වස්තුවේ ප්රවේගය සොයන්න.
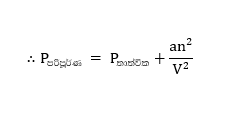
ත්වරණය
- චලනය වන වස්තුවක ප්රවේගය කාලවත් සමඟ වැඩිවන විට ත්වරණය වන්නේ යැයි කියනු ලැබේ.
- තවද, සමාන කාලාන්තර වලදී ප්රවේග වැඩිවීම සමාන නම් එය ඒකාකාර ත්වරණයෙන් ගමන් කරයි.
- එනම් වස්තුවක ත්වරණයක් ලෙස අර්ථ දක්වන්නේ ඒකක කාලයක් තුළදී ප්රවේගයේ සිදුවන වෙනස් වීමයි.
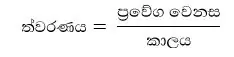
උදාහරණ 1 :- නිශ්චලතාවයෙන් ගමන් ආරම්හ කර 4 s තුලදී 40 m s-1 ප්රවේගයක් අත් කර ගන්නා වස්තුවක,

මෙසේම ප්රවේගයෙහි සිදුවන අඩුවීම “මන්දනයක්” ලෙස හඳුන්වන අතර එය ඒකාකාරව අඩුවේ නම් ඒකාකාර මන්දනයකි.
උදාහරණ 2 :- 30 m s-1 ආරම්භක ප්රවේගයකින් චලිත වන වස්තුවන් තත්පර 3 ක කාලයක් තුළ නිශ්චලතාවයටපත් වේ.

වස්තුවක් මත ක්රියාකරන a නම් ත්වරණයක් හේතුවෙන් t කාලයක් තුළදී එහි ප්රවේගය u නම් ආරම්භක අගයක සිට v නම් අවසන් අගයක් දක්වා වෙනස් වේ නම් එම වස්තුවේ ත්වරණය,

මඟින් ලැබේ.
චලිත සමීකරණ
ඒකාකාර ත්වරණයකින් සරල රේඛීය මාර්ගයක චලිත වන වස්තුවක් සළකමු. එක් එක් අවස්තාවේදී වස්තුවේ ප්රවේගය, එහි ත්වරණයටත් විස්තාපනයටත් දක්වන සම්බන්ධතාවය පහත දක්වා ඇති ලෙස සරල සමීකරණ කීපයක් මඟින් දැක්විය හැකිය. ඒවා සරල රේඛීය චලිතය සඳහා “චලිත සමීකරණ” ලෙස හැඳින්වේ.
පහත රූපයේ දක්වා ඇති ලෙස යම් වස්තුවක ප්රවේගය u නම් ආරම්භක අගයක සිට v අවසාන අගයක් දක්වා t කාලයක් තුළ ඒකාකාරව වැඩිවන අවස්තාවක් සළකමු.
මෙහිදී වස්තුවට a නම් ඒකාකාර ත්වරණයක් ලැබෙන බවත්, එම කාලය තුළ එය S දුරක් විස්තාපනය වී ඇති බවත් සැලකිය හැකිය.
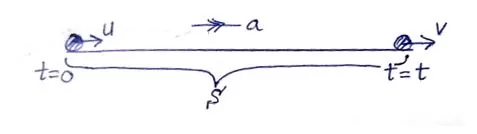
මෙම වස්තුවේ,
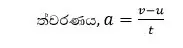
ඉහත ප්රකාශනය හරස් ගුණිතයෙන්,
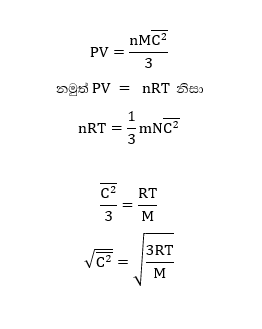
මෙහි v උක්ත කිරීමෙන්,
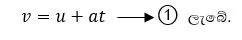
මෙම වස්තුවේ ත්වරණය ඒකාකාර බැවින් එහි,
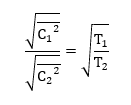
ඉහත පළමු සමීකරණයෙන් ලැබුණ සම්බන්ධය මෙයට ආදේශ කළ විට,
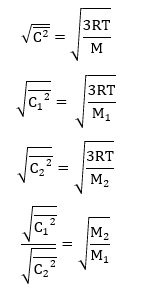
ඉහත ① සමීකරණය වර්ග කිරීමෙන්,
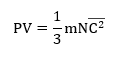
මෙය සරල රේඛාවක චලිත වන වස්තුවක චලිතය විස්තර කිරීමට යොදාගත හැකිය.



