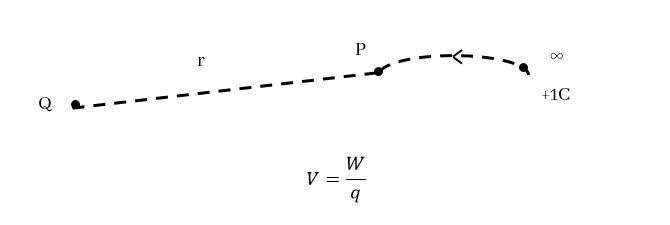
විද්යුත් ක්ෂේත්රයක සෑම ලක්ෂ්යයකටම විද්යුත් විභවයක් ඇත. අනන්තයේදී විභවය ශුන්ය ලෙස තෝරා ගනී.
Q ලක්ෂීය ආරෝපණයක සිට r දුරින් පිහිටි P ලක්ෂ්යයක විද්යුත් විභවය අර්ථ දක්වන්නේ ඒකක (+) ලක්ෂීය ආරෝපණයක් අනන්තයේ සිට මෙම ලක්ෂ්යය දක්වා ගෙන ඒමට කළ යුතු කාර්යය ලෙසය.
අනුකලනය භාවිතයෙන්;
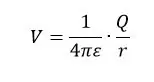
v හි ඒකකය = JC-1 = V (වෝල්ට්)
වෝල්ටය අර්ථ දැක්වීම
විද්යුත් ක්ෂේත්රයක පිහිටි එක් ලක්ෂ්යයක සිට තවත් ලක්ෂ්යයකට 1 C ක (+) ආරෝපණයක් ගෙන යාමේදී කළ යුතු කාර්යය 1 J ක් නම් එම ලක්ෂ්යයන් 2 අතර විභව අන්තරය 1V ය.
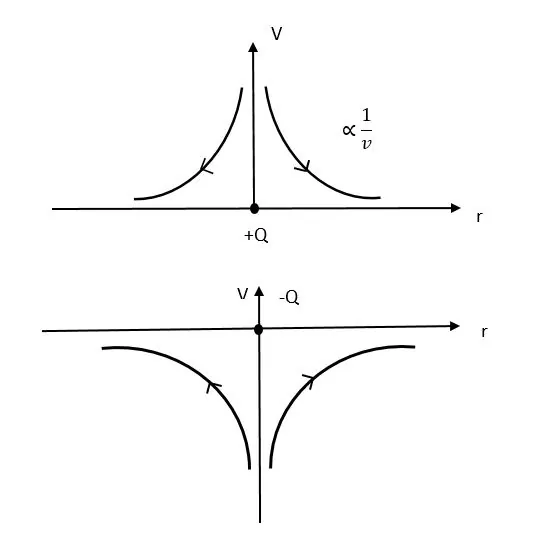
ඉහත සූතයේ Q ආදේශයේදී (+) හෝ (-) ලකුණ අනිවාර්යයෙන්ම ආදේශ කළ යුතුය. එවිට, (+)Q අවට ලක්ෂ්යයවල විභව (+) වේ. ( +q අනන්තයේ සිට ගෙන ඒමේදී +Q මගින් විකර්ෂනය කරන නිසා ලං කිරීමට සැබවින්ම කාර්යයක් කළ යුතුය)
(+)Q අවට ලක්ෂ්යයවල විභව (-) වේ. (අනන්තයේ සිට +1 C ගෙන ඒමට යාමේදී -Q විසින් ආකර්ෂණය කරන බැවින් සැබවින්ම කාර්යයක් කළ යුතු නැති නිසා)
ඉලෙක්ට්රෝන වෝල්ටය
ඉලෙක්ට්රෝනයක ආරෝපණයක් 1V විභව අන්තරයක් හරහා ගෙන යාමේදී ලබාගන්නා ශක්තිය යි.
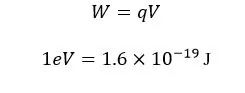
මූල ලක්ෂ්යය මත තබන ලද Q ආරෝපණයක් නිසා x අක්ෂය ඔස්සේ ඇති වන v, r සමග විචලනය වන ආකාරය සලකමු.
x අක්ෂය මත යම් පරතරයකින් තබා ඇති ලක්ෂීය ආරෝපණ දෙකකින් x අක්ෂය ඔස්සේ ඇති කරන v, r සමග විචලනය වන ආකාරය සලකමු. එහිදී එක් එක් ආරෝපණය නිසා ඇතිවන v විචලනය වෙන වෙනම ඇදගෙන ඒවා අධිස්ථාපනය කර ගත යුතුය.
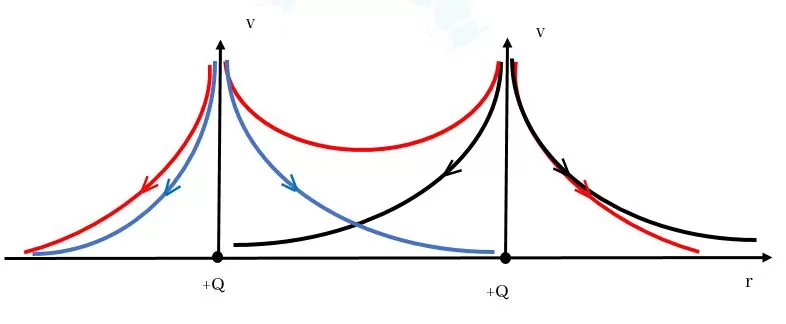
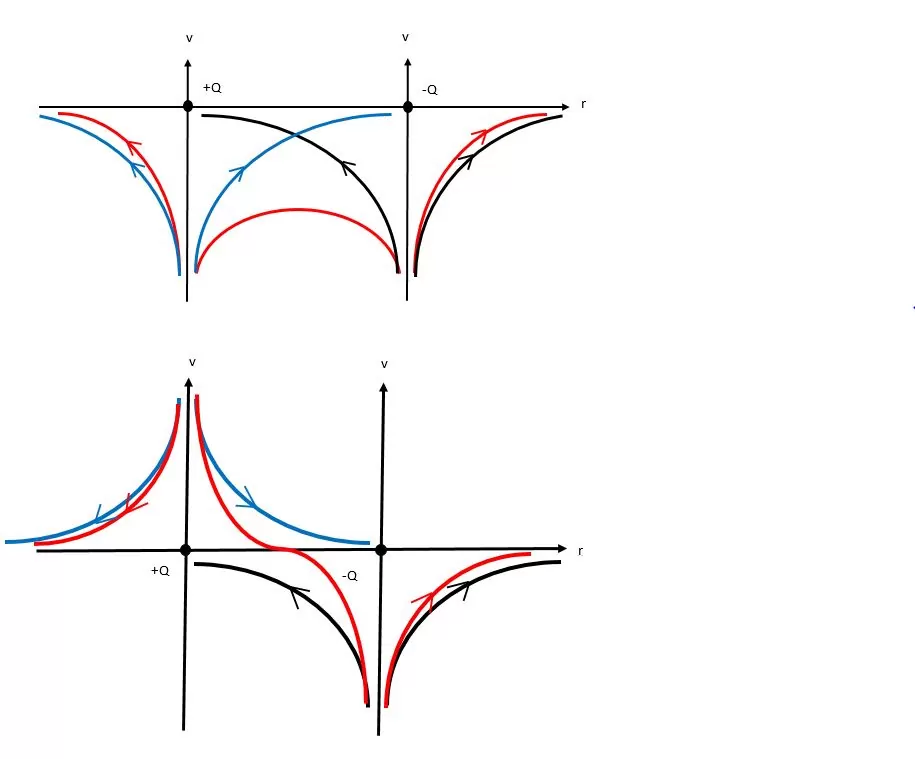
විභවය අදීශයකි. එමනිසා ආරෝපණ කිහිපයක් මගින් යම් ලක්ෂ්යයකදී ඇති කරන මුළු විභවය ගැනීමට එක් එක් ආරෝපණයෙන් ඇතිකරන විභව වෙන වෙනම ගෙන ඒවායේ එකතුව ගත යුතුය.
විභව අන්තරය
විද්යුත් ක්ෂේත්රයක ලක්ෂ්යයන් දෙකක විභවයන්ගේ වෙනස එම ලක්ෂ්යයන් දෙකේ විභව අන්තරය නම් වේ. විභව අන්තරය අර්ථ දක්වන්නේ එක් ලක්ෂ්යයක සිට අනෙක් ලක්ෂ්යයට ඒකක (+) ආරෝපණයක් ගෙන යාමට සිදුකළ යුතු කාර්යය ලෙසය.
B ට සාපේක්ෂව A හි විභවය,
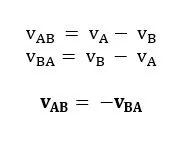
විද්යුත් විභව ශක්තිය (PE)
විද්යුත් ක්ෂේත්රයක් තුල විභවය V වන ලක්ෂ්යයක් දක්වා අනන්තයේ සිට q ලක්ෂීය ආරෝපණයක් ගෙන ඒම සඳහා qV කාර්යයක් කළ යුතුය. එය q වල විද්යුත් විභව ශක්තිය ලෙස ගබඩා වේ.
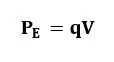
මෙහි q හා V දෙකෙහිම ලකුණවල් ආදේශ කළ යුතුය.
- (+) ආරෝපණයක් අඩු විභව ලක්ෂ්යයකදී තිබියදීට වඩා වැඩි විභව ලක්ෂ්යයකදී තිබියදී එහි විභව ශක්තිය වැඩිය.
- (-) ආරෝපණයක් වැඩි විභව ලක්ෂ්යයවල තිබියදීට වඩා අඩු විභව ලක්ෂ්යයවල තිබියදී විභව ශක්තිය වැඩිය.
q ලක්ෂීය ආරෝපණය තැබුවේ Q ලක්ෂීය ආරෝපණයේ සිට r දුරකින් නම්,
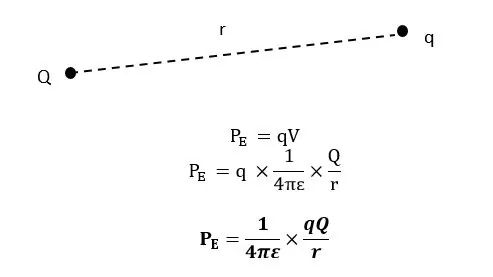
මෙහි q හා Q වල ලකුණවල් ආදේශ කළ යුතුය.
කාර්යය (W)
විද්යුත් ක්ෂේත්රයක එක් ලක්ෂ්යයක සිට තවත් ලක්ෂ්යයකට ආරෝපණයක් ගෙන යාමේදී සිදුවන විභව ශක්ති වැඩි වීමට සමාන ප්රමාණයක කාර්යයක් කළ යුතුය.
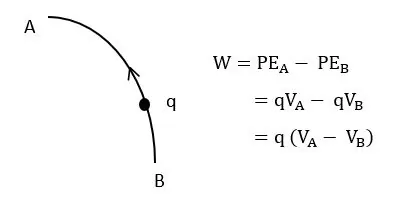
ආරෝපණයක් ගෙන යාමට සිදු කළ යුතු කාර්යය එය ගෙන යන මාර්ගයෙන් ස්වායත්තය. විද්යුත් ක්ෂේත්රද සමන්යිතික බල ක්ෂේත්රයකි.
- ඕනෑම ආරෝපණයක් තම විද්යුත් විභව ශක්තිය අඩුවෙන් පවත්වා ගැනීමට කැමැත්තක් දක්වයි. එමනිසා (+) ආරෝපණ අඩු විභව ලක්ෂ්යයක සිට වැඩි විභව ලක්ෂ්යයකටද, (-) ආරෝපණ වැඩි විභව ලක්ෂ්යයක සිට අඩු විභව ලක්ෂ්යයකටද ගෙන යාමට කාර්යය කළ යුතුය.
- (+) ආරෝපණ වැඩි විභව ලක්ෂ්යයවල සිට අඩු විභව ලක්ෂ්යයවලට ඒමේදීද (-) ආරෝපණ අඩු විභව ලක්ෂ්යයක සිට වැඩි විභව ලක්ෂ්යයකට ඒමේදීද විභව ශක්තිය අඩු කර ගනී. එම අඩුවන විභව ශක්තිය තාප ශක්තිය, ආලෝකය, චාලක ශක්තිය, විභව ශක්තිය වැනි වෙනස් ශක්ති ප්රභේදයකට පරිවර්තනය වේ.
ඉලෙක්ටෝන වෝල්ට් (eV)
කුඩා විභව ශක්ති මැනීමට ඉලෙක්ටෝන වෝල්ට් භාවිතා වේ. එය අර්ථ දක්වන්නේ ඉලෙක්ටෝන එකක ආරෝපණයක් වෝල්ට් එකක විභව අන්තරය යටතේ නිදහසේ ත්වරණය වන විට එයට ලැබෙන චාලක ශක්තිය ලෙසය.
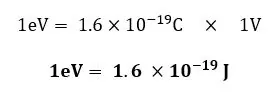
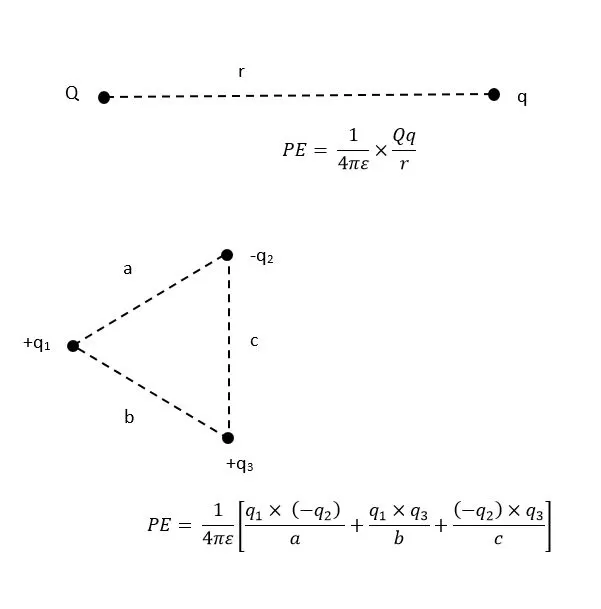
ලක්ෂීය ආරෝපණ පද්ධතියක විද්යුත් විභව ශක්තිය
ලක්ෂ්යාකාර ආරෝපණවලින් සමන්විත පද්ධතියක මුළු විද්යුත් විභව ශක්තිය යනු එක් එක් ආරෝපණයක් පිලිවෙලින් අනන්තයේ සිට නියමිත පිහිටීම් වලට ගෙන ඒමේදී කළ යුතු සුළු කාර්යයයි. එක් එක් ආරෝපණ යුගලය අතර විද්යුත් විභව ශක්ති වෙන වෙනම ගෙන එකතු කිරීමෙන් මුළු විභව ශක්තිය ලැබේ.
විද්යුත් ක්ෂේත්ර තීව්රතාව සහ විභවය අතර ඇති අන්තර්ක්රියා සම්බන්ධතාව
A (+) ආරෝපිත සහ B (-) ආරෝපිත තහඩු දෙකක් අතර (+) තහඩුව අසළ +q ආරෝපණයක් මුදා හැරියේ යැයි සිතමු.
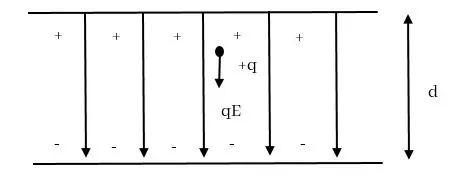
තහඩු දෙක අතර ක්ෂේත්ර තීව්රතාවය E ඒකාකාර නිසා ක්ෂේත්රයෙහි q මත නියත qE බලයක් ඇති කරයි. එම බලය යටතේ ත්වරණය වීමෙන් සෘණ තහඩුව වෙතට එනවිට q ට චාලක ශක්තියක් ලැබේ.
එය බලයෙන් සිදු කළ කාර්යය ලෙස ගත් විට Fs = qE × d ය.
අඩු වූ විද්යුත් විභව ශක්තිය ලෙස ගත් විට q = VAB ය.
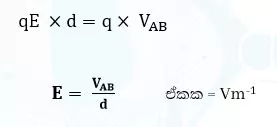
ඒකාකාර නොවන විද්යුත් ක්ෂේත්රයක එකිනෙකට ඉතා ආසන්නව dx දුරින් පිහිටි ලක්ෂ දෙකක විභව අන්තරය dv නම් එම ලක්ෂ්යයන් දෙක අතරේ,
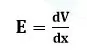
ලෙස ගත හැක.
සාමාන්යයෙන් විභව අන්තරයක් ප්රකාශ කරන්නේ අඩු විභව ස්ථානයේ සිට වැඩි විභව ස්ථානයට වන පරිදිය. E ඇත්තේ වැඩි විභව ලක්ෂ්යයේ සිට අඩු විභව ස්ථානය දෙසටය. මෙම දිශා වෙනස දැක්වීම (-) ලකුණ යෙදීමෙන්,
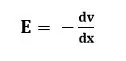
ලෙස ලියනු ලැබේ.
මෙහි dv/dx දුර x සමඟ විභවය V වෙනස් වීමේ ශීඝ්රතාවය වේ. එය විභව අනුක්රමණය ලෙස හැඳින්වේ. එය x සමඟ V ප්රස්තාරයක අනුක්රමණයද වේ.
විද්යුත් ක්ෂේත්රයක x දිශාව ඔස්සේ V-x ප්රස්තාරය භාවිතයෙන් E-x ප්රස්තාරය ලබාගන්නා ආකාරය සලකමු.
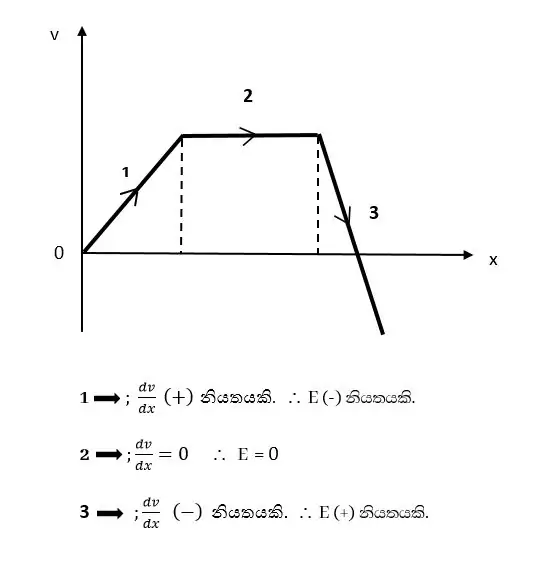
වඩා අනුකමණය වැඩි නිසා වඩා හි විශාලත්වය වැඩිවේ.
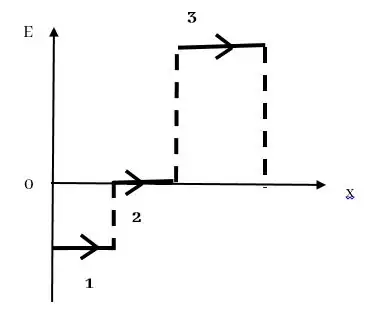
යම්කිසි පදේශයක් පුරා නියතව පවතී නම් ( + අගයක හෝ – අගයක හෝ ශුනයයේ ) එම පදේශය පුරා E=0 ය.
සම විභව පෘෂ්ඨ
විද්යුත් ක්ෂේත්රයක පිහිටි විභව සමාන ලක්ෂ යා කරන පෘෂ්ඨයක් සම විභව පෘෂ්ඨයකි. එකම සම විභව පෘෂ්ඨය මත පිහිටි ලක්ෂ දෙකක් අතර විභව අන්තරයක් නැත. එමනිසා එවැනි ලක්ෂ දෙකක් අතරේ ආරෝපණයක් ගෙන යාමට කාර්යයක් කළ යුතු නැත.
එකම සම විභව පෘෂ්ඨයක් ඔස්සේ V එකම නිසා dv/dx = 0 ය. එමනිසා සමවිභව පෘෂ්ඨයක් දිගේ විද්යුත් ක්ෂේත්රයක් තිබිය නොහැක. එමනිසා E තිබිය යුත්තේ සමවිභව පෘෂ්ඨයට ලම්බ වන සේය. එනම් තල රේඛා සහ සමවිභව පෘෂ්ඨ එකිනෙකට ලම්බ වේ.







