නිදසුන්
- 13 වසර අවසාන වාර විභාගයේදී පළමුවෙනියා වූ ශිෂ්යයයෙක් උසස් පෙළ විභාගයේදී A සාමාර්ථ තුනක් ලබා ගැනිම.
- පාසලේ ශිෂ්ය නායිකාවක් උසස් පෙළ විභාගය සමත් වීම.
මෙහිදී එක් සිද්ධියක් (A) සිදු වූ බව දී ඇති විට, අනෙක් සිද්ධිය (B) සිදුවීමේ සම්භාවිතාව සළකන බැවින් ඉහත අර්ථ දැක්වීමේ නියැදි අවකාශය Ω, A බවට කුඩා වී ඇති අතර B සිදුවන්නේ A හා සංඝටිතවයි
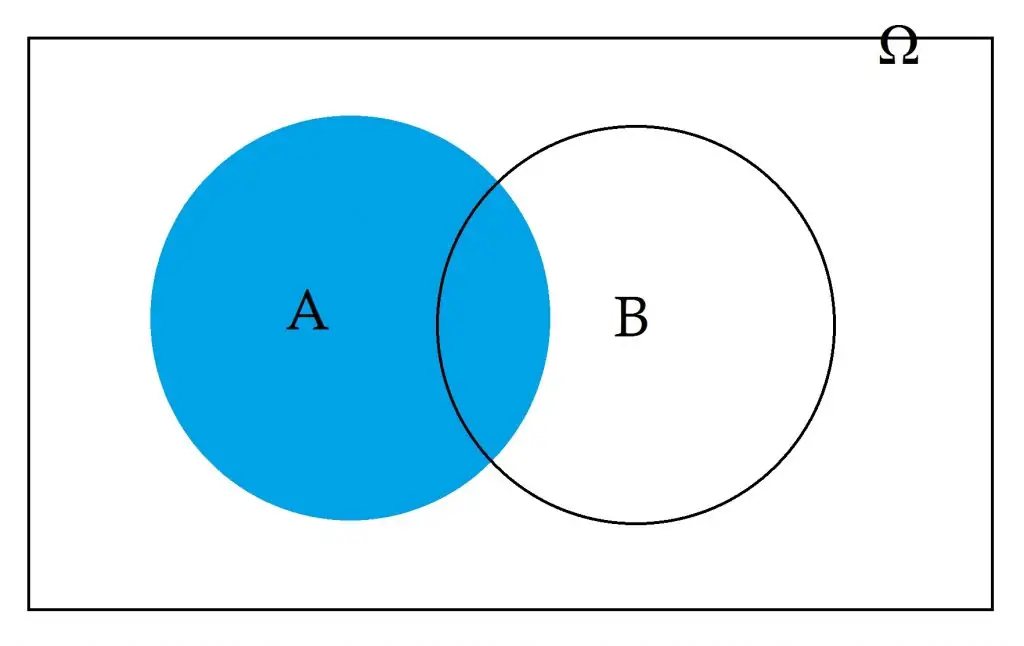
අසම්භාව්ය සම්භාවිතාව අර්ථ දැක්වීම
සසම්භාවී පරීක්ෂණයක් හා සංඝටිත Ω නියැදි අවකාශයකට අනුරූප A සිද්ධි අවකාශයේ වූ P(A)>0 ලෙස වූ A හා B සිද්ධි 2 ක් සලකමු. එවිට, A සිද්ධිය සිදු වී යයි දී ඇති විට B සිද්ධිය සිදුවීමේ අසම්භාව්ය සම්භාවිතාව P(B|A) යන්න
P(B\vert A)=\dfrac{P(B\cap A)}{P(A)};P(A)\;>\;0 ලෙස අර්ථ දැක්වේ
සටහන
\begin{array}{l}1.\;P(A)\;=\;0\;විට\;P(B\vert A)\;අර්ථ\;නොදැක්වේ.\;\\2.\;P(A\cap B)\;=\;P(A).P(B/A)\;;\;\;P(A)\;\neq\;0\;\\3.\;P(A\vert B)\;=\;\dfrac{P(A\cap B)}{P(B)}\;;\;\;P(B)\;>\;0\;\\4.\;P(A\cap B)\;=\;P(B).P(A/B)\;;\;\;P(B)\;\neq\;0\;\\5.\;P(A),\;P(B)\;\neq\;0\;විට,\\\;\;\;\;\;\;\;\;P(A\cap B)\;=\;P(A).P(B\vert A)\;=\;P(B).P(A\vert B)\end{array}නිදසුන
1 සිට 6 දක්වා අංක යෙදු දාදු කැට 2 ක් උඩ දමා ලැබෙන අය ගණන්වල එකතුව 6 ක් වේ නම්, එම අගය ගණන්වලින් එක් අගයක් 2 වීමේ සම්භාවිතාව සොයන්න.
සාධාරණ දාදු කැට 2 උඩ දැමීමේ සසම්භාවී පරීක්ෂණයට අනුරූප නියැදි අවකාශය
Ω = {(1, 1), (1, 2), (1, 3) ………………………………… (6, 6)}; n(Ω) = 36
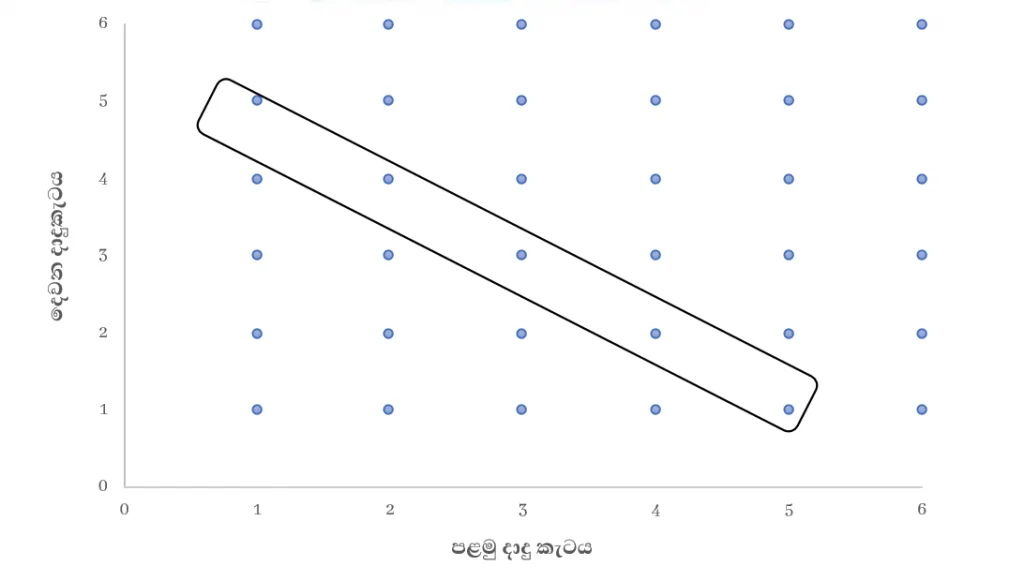
ලැබෙන අය ගණන්වල එකතුව 6 වීම = A ලෙසටද,
එක් අගයක් 2 වීම = B ලෙසටද ගනිමු.
A = { (1, 5) , (5, 1) , (2, 4) , (4, 2) , (3, 3) }
දැන් Ω නියැදි අවකාශය A බවට කුඩා වී ඇත.
\begin{array}{rcl}P(B\vert A)\;&=&\;\dfrac{P(A\cap B)\;}{P(A)};\;\;\;\;\;\;\;A\cap B\;=\;\lbrace(2,4),(4,2)\rbrace \\\; &=&\;\dfrac{\displaystyle\dfrac2{36}}{\displaystyle\dfrac5{36}};\;\;\;\;\;\;\;\;\;\;\;\;\;P(A\cap B)\;=\;\dfrac2{36}\\\;&=&\;\dfrac25\end{array}අසම්භාව්ය සම්භාවිතාව පිළිබඳ ප්රමේය
1.A යනු P(A) > 0 ලෙස වූ ඕනෑම සිද්ධියක් නම්, P(∅|A) = 0 වේ.
සාධනය :
අසම්භාව්ය සම්භාවිතාවයේ අර්ථ දැක්වීම අනුව,
\begin{array}{rcl}P(ø\vert A)\;&=&\;\dfrac{P(A\cap\varnothing)}{P(A)}\;\\&=&\dfrac{P(\varnothing)}{P(A)}\\&=&\dfrac0{P(A)}\\&=&\;0\end{array}2.A, B ∈ Ω සඳහා P(B’|A) = 1 – P(B|A) වේ.
සාධනය :
අසම්භාව්ය සම්භාවිතාවයේ අර්ථ දැක්වීම අනුව,
\begin{array}{rcl}P(B'\vert A)\;&=&\;\dfrac{P(B'\cap A)}{P(A)}\\&=&\dfrac{P(A)-\;P(A\cap B)}{P(A)}\\&=&\;1\;-\;\dfrac{P(A\cap B)}{P(A)}\\\therefore{P(B'\vert A)}\;&=&\;1\;-\;P(B\vert A)\&&\end{array}3.A1, B1, B2, ∈ Ω සඳහා P(B1|A) = P[(B1∩B2)|A] + P[(B1∩B’2)|A] වේ.
සාධනය
\begin{array}{rcl}P\lbrack(B_1\cap B_2)\vert A\rbrack\;+\;P\lbrack(B_1\cap B_2')\vert A\rbrack\;\;&=&\;\dfrac{P((B_1\cap B_2)\cap A)}{P(A)}\;+\;\dfrac{P((B_1\cap B_2')\cap A)}{P(A)}\\&=&\;\dfrac{P(B_1\cap B_2\cap A)}{P(A)}\;+\;\dfrac{P(B_1\cap B_2'\cap A)}{P(A)}\\&=&\dfrac{P(B_1\cap B_2\cap A)\;+\;{P(B_1\cap B_2'\cap A)}}{P(A)}\;\\&&\\&&\end{array}
\begin{array}{l}B_1\;\cap\;B_2\;\cap\;A\;හා\;B_1\;\cap\;B_2'\cap\;A\;අන්යෝන්ය\;වශයෙන්\;බහිෂ්කාර\;බැවින්,\;\\\;(B_1\;\cap\;B_2\;\cap\;A)\;\cup\;(B_1\;\cap\;B_2'\cap\;A)\;=\;B_1\;\cap\;A\;බැවින්,\;\\\\\end{array}
\begin{array}{rcl}P\lbrack(B_1\;\cap\;B_2\;\cap\;A)\;\cup\;(B_1\;\cap\;B_2'\cap\;A)\rbrack\;&=&\;P(B_1\cap\;A)\\P(B_1\;\cap\;B_2\;\cap\;A)\;+\;(B_1\;\cap\;B_2'\cap\;A)\;&=&\;P(B_1\cap\;A)\\P(B_1\;\cap\;B_2\;\vert A)\;+\;(B_1\;\cap\;B_2'\vert A)\;&=&\;P(B_1\vert A)\\\end{array}
\begin{array}{l}A,\;B_1,\;B_2\;\in\;Ω\;සඳහා,\\P\lbrack(\;B_1\;\cup\;B_2\;)\vert A\;\rbrack\;=\;P(\;B_1\vert A\;)\;+\;P(\;B_2\vert A\;)\;–\;P\lbrack(\;B_1\;\cap\;B_2\;)\vert A\;\rbrack\\\\\\\end{array}
සාධනය
\begin{array}{rcl}&&අසම්භාව්ය\;සම්භාවිතාව\;අර්ථ\;දැක්වීම\;අනුව,\\P\;\big\lbrack(B_1\;\cup\;B_2)\vert A\big\rbrack\;&=&\;\dfrac{P\big\lbrack(B_1\cup B_2)\cap A\big\rbrack}{P(A)}\\&=&\dfrac{P\big\lbrack(\;B_1\;\cap\;A\;)\cup(B_2\cap A)\big\rbrack}{P(A)}\\&=&\dfrac{P(\;B_1\;\cap\;A\;)+P(\;B_2\;\cap\;A\;)-P(B_1\cap A\cap B_2)}{P(A)}\\&=&\;P\;(B_1\vert A)\;+\;P\;(B_2\vert A)\;–\;P\;\big\lbrack(B_1\cap\;B_2)\vert A\big\rbrack\\&&\end{array}
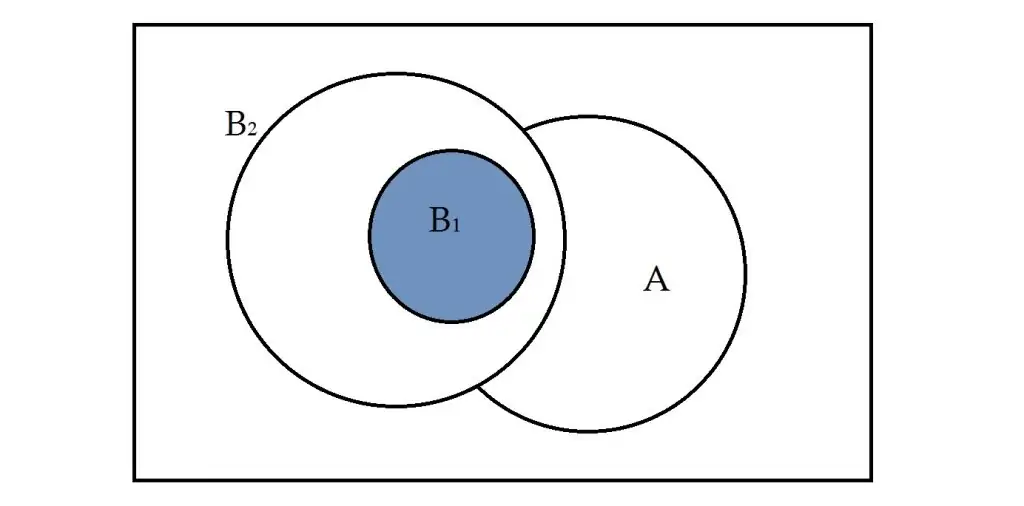
4.A, B1, B2 ∈ Ω හා B1 ⊆ B2 නම්, P (B1|A) ≤ P (B2|A) වේ
සාධනය
\begin{array}{l}B_1\;\subseteq\;B_2\;බැවින්\;(A\;\cap\;B_1)\;\subseteq\;(A\;\cap\;B_2)\;\\\therefore\;P\;(A\;\cap\;B_1)\;\leq\;P\;(A\;\cap\;B_2)\\P(A)\;˃\;0\;බැවින්\;\;\dfrac{P(A\cap B_1)}{P(A)}\;\leq\;\dfrac{P(A\cap B_2)}{P(A)}\\P\;(B_1\vert A)\;\leq\;P\;(B_2\vert A)\end{array}ගුණන නීතිය
E සසම්භාවී පරීක්ෂණයක් සමඟ සංඝටිත Ω නියැදි අවකාශයට අනුරූප A සිද්ධි අවකාශය තුළ වූ සිද්ධි 2ක් A1 හා A2 නම් හා P( A1 ) ˃ 0 වේ නම්,
P(A1∩A2 ) = P( A1 ).P( A2/A1 ) වේ.
සාධනය
\begin{array}{rcl}P\;(A_2\;\vert A_1)\;&=&\;\dfrac{P(\;A_2\cap A_1\;)}{P(A_1)}\;\\\therefore\;P\;(A_1\cap A_2)\;&=&\;P\;(A_1)\;\times P(A_2\vert A_1)\\&&\end{array}
සටහන
\begin{array}{l}A_1,\;A_{2,}\;A_3\;යනු\;ඉහත\;සිද්ධි\;අවකාශය\;තුළ\;වූ\;P\;(A_1\;\cap\;A_{}2)\;>\;0\;ලෙස\;වූ\;ඕනෑම\;සිද්ධි\;3ක්\;නම්,\\\;\;P\;(A_1\;\cap\;A_2\;\cap\;A_3)\;=\;P(A_1).P(A_2\vert A_1).P(A_{3\;}\vert A_1\cap A_2)\\උදා\;-\\P(A_1).P(A_2\vert A_1).P(A_3\;\vert A_1\cap\;A_2)\;=\;P(A_1).\;\dfrac{P(\;A_1\cap A_2\;)}{P(A_1)}.\dfrac{P(\;A_1\cap A_2\cap A_3\;)}{P(\;A_1\cap A_2\;)}\;=\;P(A_1\cap A_2\cap A_3)\\\end{array}
උදාහරණ ගැටලු –
- සාධාරණ කාසියක් දෙවරක් උඩ දැමීමේ සසම්භාවී පරීක්ෂණය සළකමු.
- පළමු වතාවේදී හිස දක්වයි නම්, වාර දෙකේදීම හිස දැක්වීමේ සම්භාවිතාව ගණනය කරන්න.
- අඩු ගණනේ එක් වාරයකදීවත් හිස දක්වයි නම්, වාර දෙකේදීම හිස දැක්වීමේ අසම්භාව්ය සම්භාවිතාව සොයන්න.
\begin{array}{l}Ω={\{(H,H),(H,T),(T,H),(T,T)}\}\\A=\{පළමු\;වතාවේදී\;හිස\;දැක්වීම\}={(H,H),(H,T)}\rightarrow P(A)=\dfrac12\\B=\{වාර\;දෙකේ\;දීම\;හිස\;දැක්වීම\}={(H,H)}\rightarrow P(B)=\dfrac14\\A\cap B={(H,H)}\rightarrow P(A\cap B)=\dfrac14\\\\\\\\\\\\\end{array}
\begin{array}{rcl}පළමු\;වතාවේදී\;හිස\;දක්වයි\;නම්,\;වාර\;දෙකේදීම\;හිස\;දැක්වීමේ\;සම්භාවිතාව\;\;&=&\;P(\;B\vert A)\\&=&\dfrac{P(A\cap B)}{P(A)}=\dfrac{\displaystyle\dfrac14}{\displaystyle\dfrac12}=\dfrac12\\C=\{අඩු\;ගණනේ\;එක්වාරයකදී\;වත්හිස\;දැක්වීම.\}={\{(H,H),(H,T),(T,H)}\}\\P\;(C)\;&=&\;\;\dfrac34\\B\cap C&=&{(H,H)}\rightarrow P(B\cap C)=\dfrac14\\අඩු\;ගණනේ\;එක්\;වාරයකදීවත්\;හිස\;දක්වයි\;නම්,\;වාර\;දෙකේදීම\;හිස\;දැක්වීමේ\;අසම්භාව්ය\;සම්භාවිතාව\;&=&\;P(\;B\vert C\;)\\&=&\dfrac{P(B\cap C)}{P(C)}\;=\;\dfrac{\displaystyle\dfrac14}{\displaystyle\dfrac34}\;=\dfrac13\\&&\\&&\\&&\\&&\;\\&&\\&&\\&&\\&&\\&&\end{array}
- වෛද්යවරයෙක් රෝගීන් 150 ක් පරීක්ෂා කිරීමේදී ඉන් 90කට හෘද රෝගද 50කට දියවැඩියාවද 30කට මෙම රෝග දෙකමද ඇති බව සොයාගන්නා ලදී. සසම්භාවී ලෙස රෝගියෙකු තෝරාගත් විට,
- ඔහු හෘද රෝගියෙකු ලෙස හඳුනාගෙන ඇති විට දියවැඩියා රෝගියෙකු වීමේ,
- ඔහු දියවැඩියා රෝගියෙකු ලෙස හඳුනාගෙන ඇති විට හෘද රෝගියෙකු වීමේ,
සම්භාවිතාව සොයන්න.
A = { පුද්ගලයෙකු හෘද රෝගියෙකු වීම. }
B = { පුද්ගලයෙකු දියවැඩියා රෝගියෙකු වීම. }
\begin{array}{rcl}P(A)\;&=&\;\dfrac{90}{150}\;=\dfrac35\;\;\\P(B)\;&=&\;\dfrac{50}{150}\;=\;\dfrac13\\P\;(A\cap B)\;&=&\dfrac{30}{150}=\dfrac15\\1.\;P\;(B\vert A)\;&=&\dfrac{P(A\cap B)}{P(A)}\;=\;\dfrac{\displaystyle\dfrac15}{\displaystyle\dfrac35}=\dfrac13\\2.P\;(A\vert B)\;&=&\;\dfrac{P(A\cap B)}{P(B)}=\;\dfrac{\displaystyle\dfrac15}{\displaystyle\dfrac13}=\dfrac35\\&&\end{array}
\begin{array}{rcl}3.P(A)\;&=&\;\frac5{12}\;\;,\;P\;(A\vert B')\;=\;\frac7{12}\;,\;P\;(A\cap B)\;=\frac18\;\;නම්,\;පහත\;සඳහන්\;සම්භාවිතා\;සොයන්න\end{array}
- P(B)
- P(A|B)
- P(B|A)
- P(B’|A)
- P(A∪B)
- P(B’|A’)
\begin{array}{rcl}1.P(A\vert B')\;&=&\;\dfrac{P(A\cap B')}{P(B')}\\\dfrac7{12}\;&=&\dfrac{P(A)-P(A\cap B)}{P(B')}\\\dfrac7{12}\;&=&\dfrac{{\displaystyle\dfrac5{12}}-{\displaystyle\dfrac18}}{P(B')}\\{P(B')}&=&\dfrac7{24}\times\dfrac{12}7\\1-P(B')\;&=&\dfrac12\\P(B)\;&=&\;\dfrac12\\&&\end{array}
\begin{array}{rcl}{1.P(A\vert B')\;}&=&\;\dfrac{P(A\cap B')}{P(B')}\\\dfrac7{12}\;&=&\dfrac{P(A)-P(A\cap B)}{P(B')}\\\dfrac7{12}\;&=&\dfrac{\displaystyle\dfrac5{12}-\dfrac18}{P(B')}\\{P(B')}&=&\dfrac7{24}\times\dfrac{12}7\\{1-P(B')\;}&=&\dfrac12\\{P(B)\;}&=&\;\dfrac12\end{array}
\begin{array}{rcl}{2.P\;(A\vert B)}&=&\dfrac{P(A\cap B)}{P(B)}=\dfrac{\displaystyle\dfrac18}{\displaystyle\frac12}=\dfrac14\end{array}
\begin{array}{rcl}{3.P\;(B\vert A)}&=&\dfrac{P(A\cap B)}{P(A)}\;=\;\dfrac{\displaystyle\dfrac18}{\displaystyle\dfrac5{12}}=\dfrac3{10}\end{array}
\begin{array}{rcl}{4.P\;(B'\vert A)}&=&{\dfrac{P(\;B'\cap A\;)}{P(A)}=\dfrac{P(A)-P(A\cap B)}{P(A)}=\;1\;-\;\dfrac{P(A\cap B)}{P(A)}=1-\;P(B'\vert A)=1-\dfrac3{10}=\dfrac7{10}}\end{array}
\begin{array}{rcl}{5.P\;(A\cup B)}&=&{P(A)\;+\;P(B)\;–\;P(A\cap B)\;=\dfrac5{12}+\dfrac12-\dfrac18=\;\dfrac{11}{12}-\dfrac18=\dfrac{19}{24}}\end{array}
\begin{array}{rcl}{6.P\;(B'\vert A')}&=&\dfrac{P(\;B'\cap A'\;)}{P(A')}\;=\dfrac{P(\;B\cup A\;)'}{P(A')}=\dfrac{1-P(A\cup B)}{1-\;P(A)}=\dfrac{1-\;{\displaystyle\dfrac{19}{24}}}{1-{\displaystyle\dfrac5{12}}}=\dfrac5{24}\times\dfrac{12}7=\dfrac5{14}\end{array}
- පෙට්ටියක රතු බෝල 5ක් හා සුදු බෝල 3ක් ඇත. වරකට 1 බැගින්,
- ප්රතිස්ථාපනය රහිතව
- ප්රතිස්ථාපනය සහිතව
බෝල 3ක් ඉවතට ගනු ලැබේ.
රතු බෝල 2ක් හා සුදු බෝල 1ක් ලැබීමේ සම්භාවිතාව සොයන්න.
මෙම පරීක්ෂණය අදියර 3කින් යුක්තය. A, B, C මඟින් පළමු, දෙවන, තුන්වන වාරවලදී රතු බෝලයක් ගැනීම පිළිවෙලින් දැක්වේ යැයි ගනිමු. එවිට, A’,B’,C’ මඟින් පළමු, දෙවන, තුන්වන වාරවලදී සුදු බෝලයක් ගැනීම පිළිවෙලින් දැක්වේ.
- ප්රතිස්ථාපනය රහිතව ගත් විට,
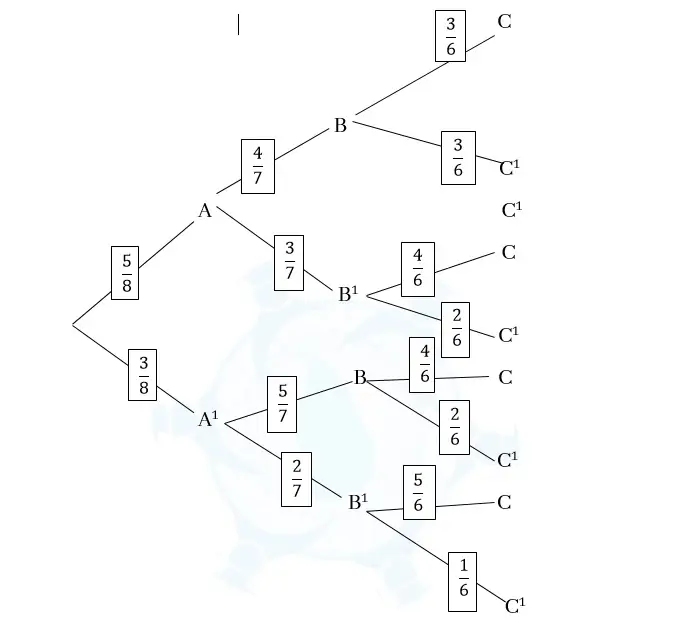
X = { රතු බෝල 2ක් හා සුදු බෝල 1ක් ලැබීම. )
X = ( A∩B∩C’ ) ( A∩B1∩C ) ( A1∩B∩C )
P(X) = P[( A∩B∩C1 ) ( A∩B1∩C ) ( A1∩B∩C )]
( A∩B∩C1 ) , ( A∩B1∩C ) , ( A1∩B∩C ) සිද්ධි අන්යෝන්ය වශයෙන් බහිෂ්කාර නිසා,
P(X) = P(A∩B∩C’) + P(A∩B’∩C) + P(A‘∩B∩C’) ; [ P(A∩B∩C’) = P(A) P(B|A) P(C’|A∩B) ]
\begin{array}{rcl}P(X)\;&=&\dfrac58\times\;\dfrac47\times\;\dfrac36\;+\;\dfrac58\;\times\dfrac37\times\;\dfrac46\;+\dfrac{\;3}8\times\;\dfrac57\times\;\dfrac46\\\;P(X)\;&=&\dfrac{\;60}{336}\;+\;\dfrac{\;60}{336}\;+\dfrac{60}{336}\\P(X)\;&=&\;\dfrac{180}{336}\\\;&=&\;\dfrac{15}{28}\end{array}
- ප්රතිස්ථාපනය සහිතව ගත් විට,
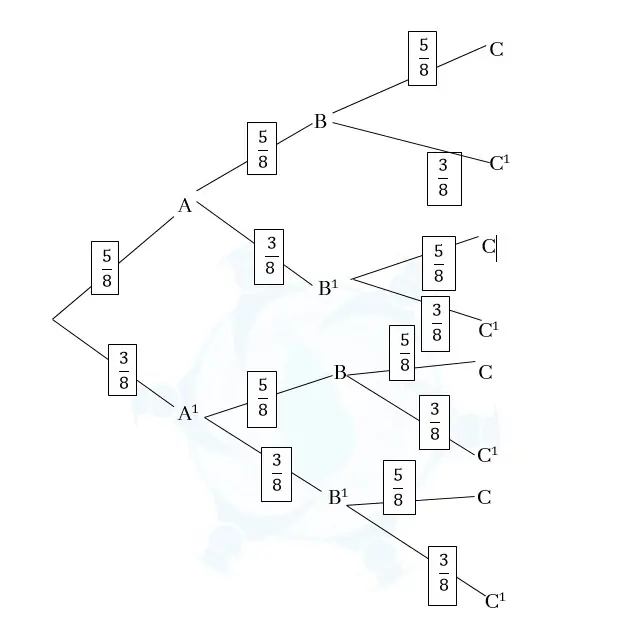
\begin{array}{rcl}P(X)\;&=&\;P\big\lbrack(\;A\cap B\cap C'\;)\;\cup\;(\;A\cap B'\cap C\;)\;\cup\;(\;A'\cap B\cap C\;)\big\rbrack\;\;\;\;\;\;\;\\\;\;\;&=&\;P(\;A\cap B\cap C'\;)\;+\;P(\;A\cap B'\cap C\;)\;+\;P(\;A'\cap B\cap C\;)\\\;\;\;\;\;\;\;\;\;&=&\dfrac{\;5}8\times\;\dfrac58\times\;\dfrac38\;\;+\;\;\dfrac58\times\;\dfrac38\times\dfrac{\;5}8\;+\;\;\dfrac38\;\times\dfrac58\times\dfrac58\\&=&\;\dfrac{225}{512}\end{array}
\begin{array}{l}5.\;එක්තරා\;රෝගියෙකු\;රෝහලකට\;නොපමාව\;ගෙන\;යාමට\;හැකි\;වීමේ\;සම්භාවිතාව\;\frac23\;කි.\;රෝගියා\;නොපමාව\\\;ගෙන\;ගියහොත්\;ඔහුව\;බේරා\;ගැනීමට\;හැකි\;වීමේ\;සම්භාවිතාව\;\frac45\;\;කි.\;පමා\;වී\;ගෙන\;ගියහොත්\\\;බේරා\;ගැනීමට\;හැකි\;වීමේ\;සම්භාවිතාව\;\frac37කි.\end{array}
- රෝගියා රෝහලට නොපමාව ගෙන ගියහොත් බේරා ගැනීමට නොහැකි වීමේ
- රෝගියා බේරා ගැනීමට හැකිවීමේ සම්භාවිතා සොයන්න.
A = { රෝගියාව නොපමාව රෝහලට ගෙන යාම. }
B = { රෝගියාව බේරා ගැනීමට හැකි වීම. }
\begin{array}{rcl}P(\;B\vert A\;)\;&=&\;\dfrac45\;\;,\;\;P(\;B\vert A'\;)\;=\;\dfrac37,\;P\;(A)\;=\;\dfrac23\\1.P(\;B'\vert A\;)\;&=&\;\dfrac{P(B'\cap A)}{P(A)}\\&=&\dfrac{P(A)-P(A\cap B)}{P(A)}\\&=&1\;-\dfrac45\\&=&\dfrac15\\2.\;\;\;\;\;\;\;P(B)\;&=&\;P(\;B\vert A'\;).P(A')\;+\;P(\;B\vert A\;).P(A)\\&=&\dfrac37\;.\dfrac13\;+\;\dfrac45.\dfrac23\\&=&\dfrac17\;+\;\dfrac8{15}\\&=&\dfrac{71}{105}\\&&\end{array}
- මලල ක්රීඩා තරගයකදී 110 m කඩුළු පැනීම හා 200 m කෙටි දුර දිවීමට ක්රීඩිකාවක් තරඟ වදියි. අතීත දක්ෂතා අනුව, කඩුළු පැනීමේ තරඟය ජය ගැනීම 0.6 ක සම්භාවිතාවක්ද කෙටි දුර ධාවනය ජය ගැනීම 0.8 සම්භාවිතාවක්ද එකම තරඟයකින්වත් ජය නොගැනීම 0.1 ක සම්භාවිතාවක්ද ඇත. මෙම ක්රීඩිකාවගේ පියා, තරඟය නැරඹීමට පැමිණෙන අවස්ථාවේ ඇය කඩුළු පැනීමේ තරඟයට සහභාගී වී පරාජයට පත් වී තිබුණි. ඇය 200 m තරඟයෙන් ජය ගනියි යැයි පියාට බලාපොරොත්තු විය හැකි සම්භාවිතාව සොයන්න.
A = { 110 m කඩුළු පැනීමෙන් ජය ගැනීම. }
B = { 200 m කෙටි දුර ධාවනය ජය ගැනීම. }
\begin{array}{rcl}P(\;A\;)\;&=&\;0.6\;,\;P(\;B\;)\;=\;0.8\;\;\\P(\;A'\cap B'\;)\;&=&\;0.1\;\;\\P(\;A\cup B\;)'\;&=&\;0.1\;(ද\;මෝගන්\;නියමය\;අනුව)\\P(\;A\cup B\;)\;&=&\;0.9\;\\P(A)\;+\;P(B)\;–\;P(A\cap B)\;&=&\;0.9\;\big\lbrack{P(\;A\cup B\;)}\;=\;{P(A)\;+\;P(B)\;–\;P(A\cap B)}\big\rbrack\\\;P(\;A\cap B\;)\;&=&\;0.6\;+\;0.8\;–\;0.9\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&=&\;0.5\\P(\;B\vert A'\;)\;&=&\dfrac{P(A'\cap B)}{P(A')}\;\\&=&\dfrac{P(B)-P(A\cap B)}{P(A')}\;\\&=&\dfrac{0.8-0.5}{1\;-\;0.6}\\&=&\dfrac34\end{array}
ඉදිරියේදී ප්රශ්න ඇතුලත් වන්නේ මෙතනටයි.

