04.02.00 – සම්භාවිතා ප්‍රමේයයන් සහ පෞරාණික අර්ථ දැක්වීම

සංයුක්ත ගණිතය 2 ප්‍රශ්න පත්‍රයේ  A ‍කොටසේ 9 වැනි ගැටලුවටද, B ‍කොටසේ  17 වන ප්‍රශ්නයේ a  ‍කොටසටද ‍මෙම පාඩමෙහි අඩංගු සිද්ධාන්ත ‍වේ.

සම්භාවිතාවයේ පෞරාණික අර්ථ දැක්වීම

\;සම්භව්‍ය\; ප්‍රතිඵලවලින්\; යුත්\; සසම්භාවී\; පරීක්ෂණයක්\; හා\; සම්බන්ධිත\; A\; නම්\; සිද්ධියක\; සම්භාවිතාව,\\ P(A) \; =\; \dfrac{n(A)}{n}\; ලෙස\; අර්ථ\; දැක්වේ.\\මෙහි \;n(A)\; යනු\; A \;සිද්ධියට\; ඇතුළත්\; සරල\; සිද්ධි\; සංඛ්‍යාවයි.\;

සටහන

\begin{array}{rcl}n\;&\geq&\;n(A)\;\geq\;0\;\;හා\;\;n\;\neq0\\ \dfrac nn&\geq&\dfrac{n(A)}n\geq0\\1\;&\geq&\;P(A)\;\geq\;0\\0\;&\leq&\;P(A)\;\leq\;1;\;n\;\neq\;0\;\end{array}

මෙහි, n(Ω) යනු නියැදි අවකාශයේ අඩංගු සියලුම අවයව ගණනද n(A) යනු A කුලකයට අයත් අවයව ගණනද වේ.

ඉහත අර්ථ දැක්වීමේ දුර්වලතා

\begin{array}{rcl}\;P(A)\; =\;\dfrac{n(A)}{n (Ω)}\; =\;\dfrac{3}{6}\; = \; \dfrac{1}{2} \\\;P(B)\; =\;\dfrac{n(B)}{n (Ω)}\; =\;\dfrac{3}{6}\; = \;\dfrac{1}{2}\\ \;P(C)\; =\;\dfrac{n(C)}{n (Ω)}\; =\;\dfrac{3}{6}\; = \; \dfrac{1}{2}\end{array}.

\begin{array}{rcl}A \cap B\;&=&\;\lbrace2\rbrace\\ P(A \cap B)\;& =& \; \dfrac{n(A\cap B)}{n(\Omega)}\\ &=&\; \dfrac{1}{6}\\B\cap C\;&=&\;\lbrace3,5\rbrace\\P(B\cap C)\;& =&\; \dfrac{n(B\cap C)}{n(\Omega)}\\&=&\;\dfrac{2}{6}\\&=&\;\dfrac{1}{3}\\ A\cup B\;&=&\;\lbrace2,3,4,5,6\rbrace\\P(A\cup B)\; &=&\; \dfrac{n(B\cup C)}{n(\Omega)}\\&=&\;\dfrac{5}{6}\\ B\cup C\;&=&\;\lbrace1,2,3,5\rbrace\\P(B\cup C)\;& =&\; \dfrac{n(B\cup C)}{n(\Omega)}\\&=&\;\dfrac{4}{6}\\&=&\;\dfrac{2}{3}\\A\cup B\cup C\;&=&\;\lbrace1,2,4,3,4,5,6\rbrace\\P(A\cup B\cup C)\;& =&\; \dfrac{n(A\cup B\cap C)}{n(\Omega)}\\&=&\;\dfrac{6}{6}\;&=&\;1\end{array}

2.“BOOK KEEPER” යන වචනයේ අකුරු සියල්ලම ගෙන වචනයක් තනනු ලැබේ. තනන ලද වචනයේ පළමු අකුර B වීමේ හා E අකුරු තුනම එකම තැන තිබීමේ සම්භාවිතාව සොයන්න.(සංකරන හා සංයෝජන පාඩමේ දැනුම භාවිත කළ යුතුය)

නියැදි අවකාශය Ω නම්,

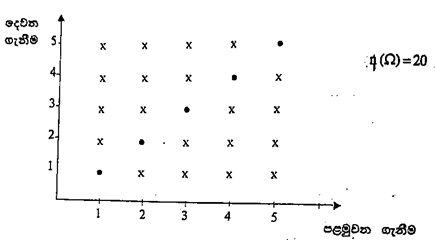
\begin{array}{l}n(Ω)\; = \; \dfrac{10!}{2!2!3!}\\තනන\; ලද\; වචනයේ\; පළමු \;අකුර\; B\; වීමේ\; සිද්ධිය\; X \;නම්,\;\\n(X)\; =\;\dfrac{9!}{2!2!3!}\\P(X)\;=\;\dfrac{n(X)}{n(Ω)}\; = \;\dfrac{\dfrac{9!}{2!2!3!}}{\dfrac{10!}{2!2!3!}}\; =\; \dfrac{1}{10}\\E\; අකුරු\; තුනම\; එක\; තැන\; ඇත්නම්\; E\; අකුරු\; තුනම\; එක\; අකුරක්\; සේ\; සළකමු.එම \;සිද්ධිය \;Y \;නම්,\\n(Y)\;=\;\dfrac{8!}{2!2!}\\P(Y)\;=\;\dfrac{n(Y)}{n(Ω)}\; =\; \dfrac{\dfrac{8!}{2!2!}}{\dfrac{10!}{2!2!3!}}\;= \; \dfrac{8!3!}{10!}\;=\; \dfrac{6}{90}\;=\; \dfrac{1}{15} \end{array}

1, 2, 3, 4, 5 යන සංඛ්‍යා ලියන ලද කාඩ්පත් අතරින් එකක් සසම්භාවීව තෝරා, දෙවැන්න ඉතිරි කාඩ්පත් 4 අතරින් තෝරා ගැනීමේ සසම්භාවී පරීක්ෂණය සළකමු. මෙම පරීක්ෂණයේ සෑම ප්‍රතිඵලයක්ම සම්භව්‍ය යැයි උපකල්පනය කර තෝරා ගන්නා කාඩ්පත්වල,

1. පළමු වතාවට ඔත්තේ අය ගණනක් ලැබීමේ,
2. දෙවන වතාවට ඉරට්ටේ අය ගණනක් ලැබීමේ,
3. එකතුව 8ක් ලැබීමේ,

සම්භාවිතාව සොයන්න.

නියැදි අවකාශය පහත ආකාරයට දක්වමු.

\begin{array}{l}පළමු\; වතාවට\; ඔත්තේ\; අය\; ගණනක්\; ලැබීම.\; = \;A\\n(A)\;=\;12\\P(A)\;=\;\dfrac{n(A)}{n(Ω)}\;=\;\dfrac{12}{20}\;=\;\dfrac{3}{5}\\දෙවන\; වතාවට\; ඉරට්ටේ\; අය\; ගණනක්\; ලැබීම.\; = \;B\\n(B)\;=\;8\\P(B)\;=\;\dfrac{n(B)}{n(Ω)}\;=\;\dfrac{8}{20}\;=\;\dfrac{2}{5}\\එකතුව\; 8ක්\; ලැබීම\; =\; C\\n(C)\;=\;2\\P(C)\;=\;\dfrac{n(C)}{n{Ω}}\;=\;\dfrac{2}{20}\;=\;\dfrac{1}{10}\end{array}

සාපේක්ෂ සංඛ්‍යාන පිවිසුම

පරීක්ෂණාත්මක සම්භාවිතාව ( සංඛ්‍යානමය අර්ථ දැක්වීම )

• යම්කිසි සසම්භාවී පරීක්ෂණයක් එකම තත්ත්වය යටතේ පුනරාවර්තනය කිරීමේදී A නම් සිද්ධිය n(A) වාරයක් සිදුවුණි නම්, ට A සිද්ධිය සිදුවීමේ සාපේක්ෂ සංඛ්‍යානය යැයි කියනු ලැබේ.
• n අපරිමිත හෝ විශාල වන විට, මෙය සීමාන්තික අගයකට එළබේ. මේ සිමාව A සිද්ධිය සිදුවීමේ පරික්ෂණාත්මක සම්භාවිතාව P(A) ලෙස අර්ථ දැක්වේ.

P(A)\;=\;\lim\limits_{n \to \infty}\bigg\lbrack \dfrac{n(A)}{n} \bigg\rbrack

සටහන

\begin{array}{l}0\leq n(A) \leq n \;බැවින්\; හා \;n \not= 0 \;බැවින්,\\0\leq\dfrac{n(A)}{n}\leq 1\\ 0 \leq P(A) \leq 1 \;වේ. \end{array}

මෙම අර්ථ දැක්වීමේ ඇති දුර්වලතා

• පරීක්ෂණයකින් තොරව සම්භාවිතාව ගණනය කල නොහැකිය.
• පරීක්ෂණය කරන වාර ගණන නිශ්චිත නැත.
• පරීක්ෂණයෙන් ලැබෙන ප්‍රතිඵල පුද්ගල බද්ධ වීම.
• පරීක්ෂණය සමාන තත්ත්ව යටතේ විශාල වාර ගණනක් සිදු නොවීම හා සිදුකළ නොහැකි වීම.

පුද්ගල බද්ධ සම්භාවිතාව

• යම් පුද්ගලයෙකුගේ විෂයන් පිළිබද දැනුම, අවබෝධය, ඔහුගේ අත්දැකීම් හා ඔහුගේ පෞද්ගලික හැගීම් භාවිතා කරමින් යම් සිද්ධියක් පිළිබද කරුණු සොයා බලා එම සිද්ධිය සිදුවීමේ සම්භාවිතාව අනුමාන ලෙස ප්‍රකාශ කිරීම පුද්ගල බද්ධ සම්භාවිතාව නම් වේ. මෙහිදී දෙනු ලබන අගයේ ( සම්භාවිතාවයේ ) විශ්වාසනීයත්වය රදා පවතින්නේ එම සම්භාවිතාව පවරනු ලබන පුද්ගලයා මත වේ. මෙහිදී සම්භාවිතාව පවරනු ලබන පුද්ගලයාට ලබාගත හැකි වූ කුමන ආකාරයේ හෝ තොරතුරු භාවිතා කළ හැකිය. එලෙස සම්භාවිතාව පැවරිය හැකි සිද්ධි ලෙස,
  • අලුතින් ව්‍යාපාරයක් ආරම්භ කිරීම.
  • යම් ආයතනයකට සහායකයෙකු තෝරා ගැනීම වැනි සිද්ධි සැළකිය හැකිය.

• මෙහිදී අලුතින් ව්‍යාපාරයක් ආරම්භ කිරීමේදී, එම ව්‍යාපාරය සාර්ථක වීමට ඇති ඉඩකඩ පිළිබදව තේරුම් ගැනීමටද ආයතනයකට සහායකයෙකු පත්කර ගැනීමේදී ඉදිරිපත් වන්නන් අතරින් වඩා සුදුසු පුද්ගලයා තෝරා ගැනීමටද පුද්ගලබද්ධ සම්භාවිතාව ඉවහල් වේ.
• නමුත්, පුද්ගලබද්ධ සම්භාවිතාව පිළිබද යම් පුද්ගලයන් දෙදෙනෙකුට එකගතාවයකට පත්වීමට ඇති අපහසුතාව නිසා මේ පිළිබද ඉගැන්වීම් කටයුතු කරනු නොලැබේ.

සම්භාවිතාවයේ ප්‍රත්‍යක්ෂමය අර්ථ දැක්වීම

• සසම්භාවී පරීක්ෂණයක් සමග සංඝටිත Ω නියැදි අවකාශයකට අනුරූප සිද්ධි අවකාශය A  යැයි ගනිමු.
• එවිට, පහත දැක්වෙන ප්‍රත්‍යක්ෂ තෘප්ත කරන වසම A  වුත් සහවසම ( 0,1 ) වුත්, P( ) නම් ශ්‍රිතය සම්භාවිතා ශ්‍රිතය ලෙස හැදින්වේ.

1. ඕනෑම\;  A \in A  සදහා\; P(A) \geq  0
2. P(Ω) = 1
3. A_1,A_2\;යනු \;A \;තුළ \;අන්‍යෝන්‍ය \;වශයෙන්\;බහිෂ්කාර\; සිද්ධි\; 2 \;ක් \;නම්, \;P(A_1 \cup A_2)\; =\; P(A_1) + P(A_2) \;වේ.

• මෙම අර්ථ දැක්වීම සම්භාවිතාව පිළිබද ගණිතමය අර්ථ දැක්වීමයි. කවර ශ්‍රිතයක්, සම්භාවිතා ශ්‍රිතයක් වේද යන්න මෙම අර්ථ දැක්වීම මගින් දක්වයි.

සටහන

• සසම්භාවී පරීක්ෂණයක වූ A නම් සිද්ධියක් සදහා P( ) ශ්‍රිතය ගන්නා අගය P(A) මගින් දැක්වෙන අතර එයින් A සිද්ධිය සිදුවීමේ සම්භාවිතාව දක්වයි.
• P( ) ශ්‍රිතයේ පරාසය A සිද්ධි අවකාශය තුළ වූ විය හැකි සියලු සිද්ධිවලට අනුරූප සම්භාවිතාවන්ගෙන් යුක්ත වේ.

ප්‍රතිඵලය

A₁, A₂…, A_n යනු සිද්ධි අවකාශයේ අන්‍යෝන්‍ය වශයෙන් බහිෂ්කාර සිද්ධි අනුක්‍රමයන් නම්,

P\Big(\bigcup \limits_{i=1}^n A_i\Big)\;=\; \sum\limits_{i=1}^nP(A_i)

සම්භාවිතාව පිළිබද ප්‍රමේයය

ප්‍රමේයය 1

අභිශුන්‍ය සිද්ධිය සිදුවීමේ සම්භාවිතාව  ශුන්‍ය වේ. එනම්, P(Ф) = 0 වේ.

සාධනය

\begin{array}{rcl}&&සසම්භාවී\;පරීක්ෂණයක්\;හා\;සංඝටිත\;නියැදි\;\;අවකාශය\;\Omega\;ලෙස\;ගනිමු.\\Ω\;&=&\;Ф\cupΩ\\P(Ω)\;&=&\;P\;(Ф\;\cup\;Ω\;)\\Ф\;\cap\;Ω\;&=&\;Ф,\;නිසා\;Ф\;සහ\;Ω\;අන්‍යෝන්‍ය\;වශයෙන්\;බහිෂ්කාර\;බැවින්\;3\;වන\;ප්‍රත්‍යක්ෂය\;අනුව,\\P(Ω)\;&=&\;P(Ф)\;+\;P(Ω)\\ \therefore\;P(Ф)\;&=&\;0\end{array}

ප්‍රමේයය 2

• සසම්භාවී පරීක්ෂණයක් සමග සංඝටිත Ω නියැදි අවකාශයකට අනුරූප A සිද්ධි අවකාශය තුළ වූ A නම් සිද්ධියක් සළකමු.
• A හි අනුපූරක සිද්ධිය A’වේ නම්, P(A’) = 1 – P(A) වේ.

සාධනය

\begin{array}{rcl}Ω\;&=&\;A\;\cup\;A'\\P(Ω\;)\;&=&\;P\;(A\;\cup\;A')\\A\;\cap\;A'\;&=&\;Ф\;නිසා\;A\;හා\;A'\;අන්‍යෝන්‍ය\;වශයෙන්\;බහිෂ්කාර\;වේ.\\P\;(A\;\cup\;A')\;&=&\;P(A)\;+\;P(A')\\P(Ω)\;&=&\;P(A)\;+\;P(A')\\1\;&=&\;P(A)\;+\;P(A')\\P\;(A')&=&\;1\;–\;P(A)\end{array}

ප්‍රමේයය 2 හි A = Ω යොදමු.

\begin{array}{rcl}එවිට,A'\;&=&\;Ф\\P(Ф)\;&=&\;1\;–\;P(Ω)\\P(Ф)\;&=&\;1\;–\;1\;;\;ප්‍රත්‍යක්ෂය\;අනුව\;P(Ω)\;=\;1\;නිසා,\\P(Ф)\;&=&\;0\;;\;\;එනම්\;ප්‍රමේයය\;2\;භාවිතයෙන්\;ප්‍රමේයය\;1\;ලබාගත\;හැකි\;වේ.\end{array}

ප්‍රමේයය 3

සසම්භාවී පරීක්ෂණයක් සමග සංඝටිත Ω නියැදි අවකාශයට A අනුරූප සිද්ධි අවකාශය තුළ වූ ඕනෑම සිද්ධි 2ක් A හා B ලෙස ගනිමු.

එවිට, P(A) = P( A ∩ B ) + P( A ∩ B’ ) වේ.

සාධනය

\begin{array}{rcl}&&A\;\cap\;B\;හා\;A\;\cap\;B'\;යනු\;අන්‍යෝන්‍ය\;වශයෙන්\;බහිෂ්කාර\;සිද්ධි\;වන\;අතර,\\\;A\;&=&\;\lbrack(A\cap B)\;\cup\;(A\;\cap\;B')\rbrack\\දැන්,\;P(A)\;&=&\;P\;\lbrack(A\;\cap\;B)\;\cup\;(A\;\cap\;B')\rbrack\\3 \;ප්‍රත්‍යක්ෂය\; අනුව,\\P(A)\; &=&\; P \big\lbrack(A ∩ B)\; +\; (A ∩ B')\big\rbrack\\&&\end{array}

ප්‍රමේයය 4

P (A ∪ B) = P(A) + P(B) – P (A ∩ B)වේ.

සාධනය

\begin{array}{rcl}(A\;\cap\;B')\;හා\;B\;අන්‍යෝන්‍ය\;වශයෙන්\;බහිෂ්කාර\;බව\;පැහැදිලිය.\\තවද,(\;A\;\cap\;B')\;\cup\;B\;&=&\;A\;\cup\;Bවේ.\\\therefore\;P\;(A\;\cup\;B)\;&=&\;P\;\big\lbrack\;(A\;\cap\;B')\;\cup\;B\big\rbrack\\3\;වන\;ප්‍රත්‍යක්ෂය\;අනුව,\\P\;(A\;\cup\;B)\;&=&\;P\;(A\;\cap\;B')\;+\;P(B)\;\longrightarrow\;①\\ප්‍රමේයය\;2\;අනුව,\\P(A)\;&=&\;P(A\;\cap\;B'\;)\;+\;P(A\;\cap\;B\;)\;\longrightarrow\;②\;\\①-②\;&\Longrightarrow\\P\;(A\;\cup\;B)\;–\;P(A)\;&=&\;P(B)\;-\;P\;(A\;\cap\;B)\\P\;(A\;\cup\;B)\;&=&\;P(A)\;+\;P(B)\;-\;P\;(A\;\cap\;B)\end{array}

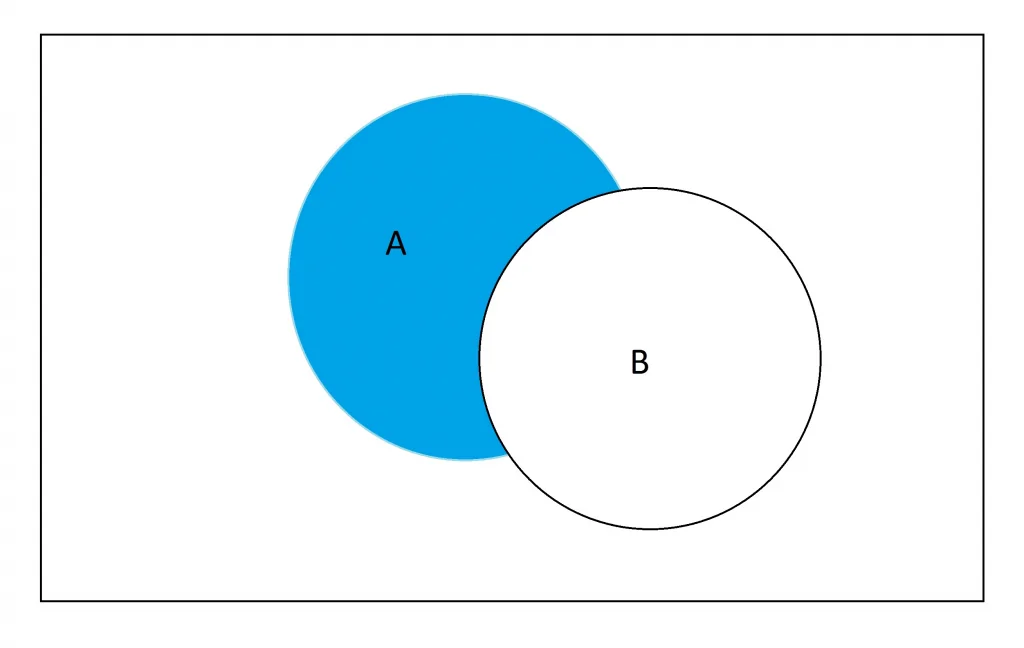
ප්‍රමේයය 5

A ⊆ B නම්,P(A) ≤ P(B)

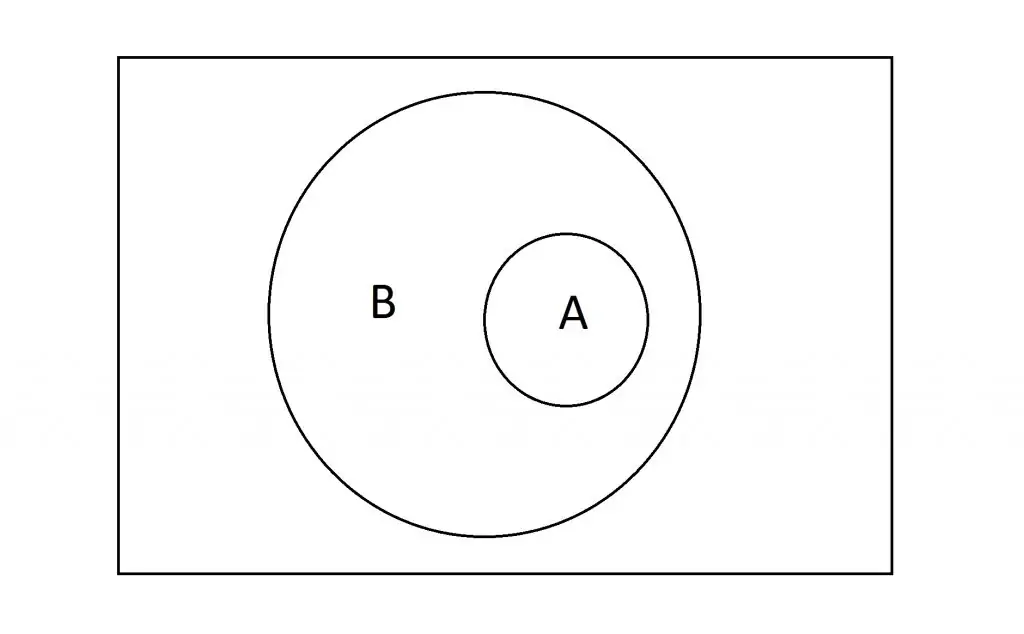
සාධනය

\begin{array}{rcl}A\;&\subseteq&\;B\;බැවින්,\\B\;&=&\;A\;\cup\;(A'\;\cap\;B)\\\therefore\;P\;(B)\;&=&\;P\;\big\lbrack A\;\cup\;(A'\;\cap\;B)\big\rbrack\\A\;හා\;\;A'\;\cap\;Bඅන්‍යෝන්‍ය\;වශයෙන්\;බහිෂ්කාර\;බැවින්\;3\;වන\;ප්‍රත්‍යක්ෂය\;අනුව,\\P\;(B)\;&=&\;P\;(A)\;+\;P\;(A'\;\cap\;B)\\P(B)\;-\;P(A)\;&=&\;P\;(A'\;\cap\;B)\\නමුත්,\;1\;වන\;ප්‍රත්‍යක්ෂය\;අනුව,\\P\;(A'\;\cap\;B)\;&\geq&\;0\\P(B)\;–\;P(A)\;&\geq&\;0\\P(B)\;&\geq&\;P(A)\\P(A)\;&\leq&\;P(B)\\මෙහි\;සමානතාව\;රදා\;පවතින්නේ\;P(\;A'\;\cap\;B\;)\;&=&\;0\;වන\;විටදීය\\එනම්,\;A'\;\cap\;B\;&=&\;Ф\;විටදීය.\\එනම්,\;A\;&=&\;B\;විටදීය.\\ඉහත\;ප්‍රමේයයේ\;විලෝමය\;සාධාරණව\;සත්‍ය\;නොවේ.\end{array}

• එනම්, P(A) ≤ P(B) විට, සාධාරණව A ⊆ B නොවේ.
• උදාහරණයක් මගින්, විලෝමය සාධාරණව සත්‍ය නොවන බව පෙන්වමු.
• සාධාරණ දාදු කැටයක් උඩ දමා මතුපිටට වැටෙන අගය නිරීක්ෂණය සළකමු.

Ω = { 1, 2, 3, 4, 5, 6 }

A යනු ඉරට්ටේ අගයක් ලැබීමේ සිද්ධියද

B යනු 5ට අඩු අගයක් ලැබීමේ සිද්ධියද යැයි ගනිමු.

\begin{array}{rcl}A\;&=&\; \lbrace 2,4,6\rbrace\\B\;&=&\;\lbrace1,2,3,4\rbrace\\ P(A)\;&=&\;\dfrac{3}{6}\;,\;P(B)\;=\;\dfrac{4}{6}\\මෙහි, P(A) \;&<& \;P(B) \;බව\; පැහැදිලිය.\\නමුත්, A &⊆&B\; බවද\; පැහැදිලිය\\∴ P(A) \; & \leq& \;P(B) \;වූ\; විට\; සාධාරණව\; A ⊆ B\; නොවේ.\end{array}.

උදාහරණ ගැටලු –

\begin{array}{l}1.A \;හා\; B\; යනු\; P(A)\;=\;\dfrac{1}{2},P(A∪B)\;=\;\dfrac{3}{4} ,P(B')\;=\;\dfrac{5}{8} වන\; සේ\; වූ\; සිද්ධි\; 2\; ක්\; නම්, \\P(A∩B), P(A'∩B'),P(A'∪B'),P(B∩A') \;ගණනය\; කරන්න.\end{array} \begin{array}{rcl}P(B)\;& =& \;1 – P(B')\\&=&\; 1 - \dfrac{5}{8}\\&=&\; \dfrac{3}{8}\\P(A∪B) \;&=&\; P(A) + P(B) – P(A∩B)\\\dfrac{3}{4} \;&=&\; \dfrac{1}{2}+ \dfrac{3}{8}-P(A∩B)\\P(A∩B)\;&=&\; \dfrac{7}{8}-\dfrac{6}{8}\\&=&\; \dfrac{1}{8}\\ද\; මෝගන් \;නියමය\; අනුව,\\A' ∩ B'&=& (A∪B )' \\P (A' ∩ B')\; &=&\; P (A∪B )'\\ &=& \;1 – P (A∪B)\\ &=&\; 1 – \dfrac{3}{4} \\&=&\dfrac{1}{4}\\P(B) \;&=&\; P(A∩B) + P(A'∩B)\\ \dfrac{3}{8}\; &=&\; \dfrac{1}{8} + P(A'∩B)\\ P(A'∩B)\; &=&\; \dfrac{2}{8}\\&=&\; \dfrac{1}{4}\end{array}

2.ඉහත ප්‍රමේයය වලින් ආරම්භ කරමින්, 𝑃 (𝐴 ∪ 𝐵 ∪ 𝐶) = 𝑃(𝐴) + 𝑃(𝐵) + 𝑃(𝐶) − 𝑃(𝐴∩𝐵) − 𝑃(𝐵∩𝐶) − 𝑃(𝐶∩𝐴) + 𝑃(𝐴∩𝐵∩𝐶) බව පෙන්වන්න.

\begin{array}{rcl}P(A\cup B\cup C)&=&P(A\cap D)\;\;\;මෙහි\;D=B\cup C\;\\&=&P(A)+P(D)-P(A\cap D)\\&=&P(A)+P(B\cup C)–P\lbrack A\cap(B\cup C)\rbrack\\&=&P(A)+P(B)+P(C)-P(B\cap C)–P\lbrack A\cap(B\cup C)\rbrack\\&=&P(A)+P(B)+P(C)-P(B\cap C)–P\lbrack(A\cap B)\cup(A\cap C)\rbrack\\&=&P(A)+P(B)+P(C)-P(B\cap C)–{P(A\cap B)+P(A\cap C)-P\lbrack(A\cap B)\cap(A\cap C)\rbrack}\\&=&P(A)+P(B)+P(C)-P(B\cap C)–P(A\cap B)-P(A\cap C)+P(A\cap B\cap C)\\&=&P(A)+P(B)+P(C)-P(A\cap B)-P(B\cap C)-P(C\cap A)+P(A\cap B\cap C)\end{array}

3.A ,B, C නම් අශ්වයින් තිදෙනෙක් තරගයට දුවති. A ගේ දිනීමේ හැකියාව, B ගේ දිනීමේ හැකියාව මෙන් දෙගුණයකි. B ගේ දිනීමේ හැකියාව C ගේ දිනීමේ හැකියාව මෙන් දෙගුණයකි. අශ්වයින් දෙදෙනෙකු හෝ තිදෙනාම එකවර ජයගත නොහැකි නම්, තරගයෙන් B හෝ C දිනීමේ සම්භාවිතාව සොයන්න.

A දිනීමේ සිද්ධිය A ලෙසද

B දිනීමේ සිද්ධිය B ලෙසද

C දිනීමේ සිද්ධිය C ලෙසද අර්ථ දක්වමු.

එවිට, P( C ) = x නම්, P(B) = 2x හා P(A) = 4x වේ.

\begin{array}{rcl}P\;(A\;\cup\;B\;\cup\;C)\;&=&\;P(A)\;+\;P(B)\;+\;P(C)\\P\;(Ω)\;&=&\;4x\;+\;2x\;+\;x1\;\\&=&\;7x\\x\;\;\;\;&=&\;\;\dfrac17\\P\;(C)\;&=&\;\;\dfrac{\;1}7\;\;,P(B)\;=\;\;\;\dfrac{2\;}7,P(A)\;=\;\;\;\dfrac47\\ P\;(B\;\cup\;C)\;&=&\;P(B)\;+\;P(C)\\&=&\;\;\dfrac17+\;\;\;\dfrac27\\&=&\;\;\dfrac37\end{array}

4.A හා B සිද්ධි ද A හා C සිද්ධි ද අන්‍යෝන්‍ය වශයෙන් බහිෂ්කාර වේ. P(B)= 0.4, P (A ∪B)=0.5 ,P(A ∪C) = 0.6,P (B ∪ C) = 0.8,P (A ∪ B ∪ C) = 0.9 වේ.

1. P (B∩C)
2. P(A∩B∩C) සොයන්න.

\begin{array}{rcl}&&\;\;A\;හා\;B\;සිද්ධි\;අන්‍යෝන්‍ය\;වශයෙන්\;බහිෂ්කාර\;නිසා,\\P\;(A\;\cup\;B)\;&=&\;P(A)\;+\;P(B)\;;\;(A\cap B)\;=\;Ф\\0.5\;\;\;&=&\;P(A)\;+\;0.4\;\\P(A)\;&=&\;0.1\\&&\;A\;හා\;C\;සිද්ධි\;අන්‍යෝන්‍ය\;වශයෙන්\;බහිෂ්කාර\;නිසා,\\P\;(A\;\cup\;C)\;&=&\;P(A)\;+\;P(C)\;;\;(A\cap C)\;=\;Ф\\0.6\;\;\;&=&\;0.1\;\;\;\;+\;P(C)\;\\P(C)\;&=&\;0.5\\P(B\cap C)\;&=&\;P(B)\;+\;P(C)\;–\;P(B\cup C)\;\;\;\;\;\;\;\;\;\\&=&\;0.4\;+\;0.5\;–\;0.8\;\;\;=\;0.1\;\\\;\;P(A\cap B\cap C)\;&=&\;P\lbrack(A\cap B)\;\cap\;(A\cap C)\rbrack\;\\&=&\;P(Ф\cap Ф)\;\\&=&\;P(Ф)\;\;\;\;\;\\&=&\;0\;\;\;\;\;\;\;\;\;\;\;\;\end{array}

A_1, A₂, A₃, … A_n යනු Ω නියැදි අවකාශයට අනුරූප A සිද්ධි අවකාශයේ ඇති අන්‍යෝන්‍ය වශයෙන් බහිෂ්කාර සිද්ධි n ගණනකි.

P(A_1\cup A_2\cup A_3\cup\dots\cup A_n)\;=\;\sum_{r=1}^nP(A_r)

 බව පෙන්වන්න

දාදු කැටයක් උඩ දැමු විට r වන අංකය උඩු අතට සිටින සේ එම කැටය වැටීමේ සම්භාවිතාව  P(r) , r ට සමානුපාතික වන ලෙස එම කැටය හරණය කර ඇත.

මෙහි r = 1, 2, 3, 4, 5, 6 වේ.

1. P (r)
2. ඔත්තේ අංකයක් ලැබීමේ සම්භාවිතාව
3. මෙම කැටය දෙවරක් උඩ දැමුවේ නම්, ලැබෙන අංකවල එකතුව 10ට වැඩි වීමේ සම්භාවිතාව සොයන්න.

\begin{array}{rcl}P(A_1\cup A_2\cup A_3\cup\dots\cup A_n)\;&=&\;P(A_1)+P(A_2)+P(A_3)+\cdots+P(A_n)(A_1\cap A_2\cap A_3\cap\dots\cap A_n=Ф)\\&=&\sum\limits_{r\;=1}^nP(A_r)\end{array} \begin{array}{rcl}&&\;P(r)\;\infty\;r\\;\therefore\;P(r)&=&\;kr\;;\;k\;-\;නියතයකි\\&&මෙහි\;\sum_{r=1\;}^6P(A_r) \;=\; 1\end{array} \begin{array}{rcl}1.\;P\;(1)\;+\;P\;(2)\;+\;P\;(3)\;+\;P\;(4)\;+\;P\;(5)\;+\;P\;(6)\;&=&\;1\;k\;+\;2k\;+\;3k\;+\;4k\;+\;5k\;+\;6k\\&=&\;1\\21k\;&=&\;1\\k\;&=&\dfrac{\;\;1\;}{21}\\\therefore\;P\;(r)\;&=&\;\;\dfrac{\;\;1\;}{21}\end{array} \begin{array}{rcl}2.\;P(1\cup\;3\cup5)\;&=&\;P\;(1)\;+\;P\;(3)\;+\;P\;(5)\&=&\dfrac{\;\;1}{21}+\dfrac{3\;\;}{21}+\;\;\dfrac5{21}\\&=&\;\dfrac9{21}\\&=&\;\dfrac37\end{array} \begin{array}{rcl}3.\;\;P\;(එකතුව\;10\;ට\;වැඩි\;වීම)\;&=&\;\;P(\;6,5\;)\;+\;P(\;5,6\;)\;+\;P(\;6,6\;)\\&=&\;\;\;\;\dfrac6{21}\;\times\dfrac5{21}+\dfrac5{21}\;\times\dfrac6{21}+\dfrac6{21}\;\times\dfrac6{21}\\&=&\;\dfrac27\;\times\dfrac{16}{21}\\&=&\;\dfrac{32}{147}\;\end{array}