අනාකුල ප්රවාහය
- තරල ප්රවාහයක ඕනෑම ලක්ෂ්යයක් පසු කරන තරල අංශුවක ප්රවේගය කාලයත් සමඟ වෙනස් නොවේ නම්, එම ප්රවාහය අනාකුල හෙවත් නොසැලෙන ප්රවාහයක් ලෙස හඳුන්වයි.
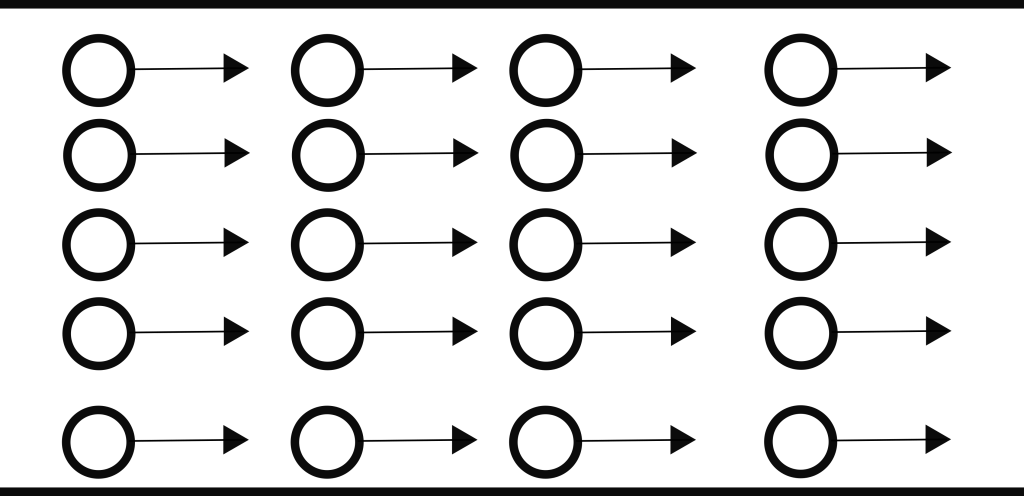
- අනාකුල රේඛාවකට යම් ලක්ෂ්යයකදී අඳිණු ලබන ස්පර්ශකය මගින් එම ලක්ෂ්යයකදී ප්රවාහ ප්රවේගයේ දිශාව ලැබේ.
- තරල ප්රවාහයක් ගලා යන විට එය අනාකුල ප්රවාහයකි. එනම් තරල අංශු එකක් පිටුපස එකක් අනුපිළිවෙලින් නියමිත රේඛා වැස්සේ ගලා යයි. තරල අංශු ගලායන මෙම රේඛා අනාකුල රේඛා ලෙස හැදින්වේ. මෙම අනාකුල රේඛා කිසිවිටෙකත් එකිනෙකා නොකපයි. අනාකුල ප්රවාහයක තරල අංශු වල ප්රවේගය කුඩාය.
- එහි ප්රවේගය වැඩිකරගෙන යාමේදී එක්තරා ප්රවේගයක් ඉක්මවා යනවාත් සමග අනාකුල ප්රවාහය බිද වැටි එය ආකුල වේ. එමනිසා තරලයකට අනාකුලව ගලායාහැකි ප්රවේගය “ආන්ත ප්රවේගය” ලෙස හැදින්වේ.
ආකුල ප්රවාහය
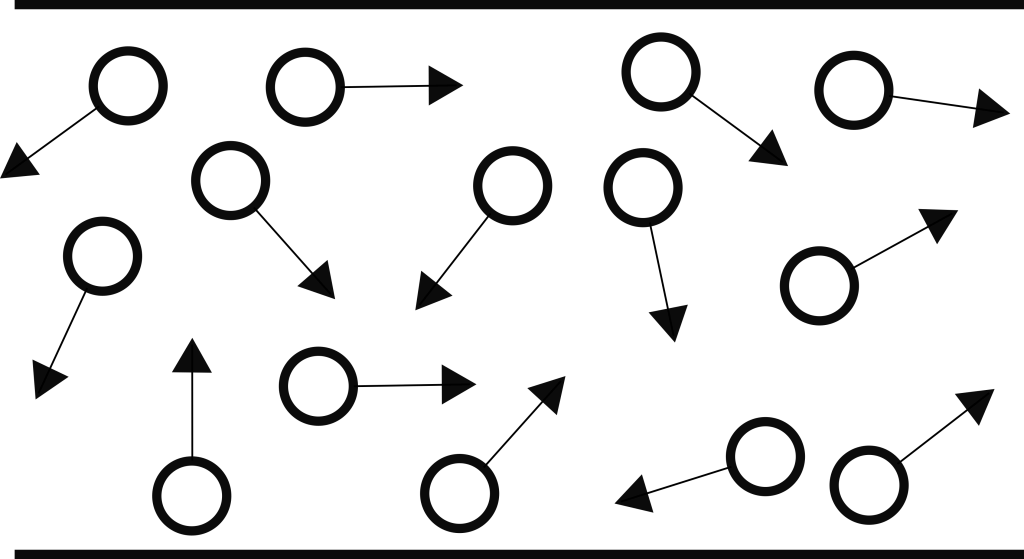
- කැළඹිලිකාරී ප්රවාහය ආකුල වේ. එනම් තරල අංශු කිසිම පිළිවෙලක් නොමැතිව සසම්භාවිව විවිද දිශා ඔස්සේ විවිධ ප්රවේග වලින් චලනය වේනම් ඒක ආකුල ප්රවාහයකි.
- මෙවැනි ප්රවාහයක් තරල අංශු වල ප්රවේගය තරමක් වැඩිය. එම නිසා චාලක ශක්තිය වැඩිය.
දුස්ස්රාවි තරල හා සුස්ස්රාවි තරල
- සන්සුන්ව ගලායන තරල ප්රවාහයක් ආස්තරිය ප්රවාහයකි. එනම් ද්රවස්තර ලෙස ගලා යයි. මෙම ද්රවස්ථර වල ප්රවේග එකිනෙකට වෙනස්ය. එම නිසා යාබද ස්ථර 2 ක් අතර සාපේක්ෂ ප්රවේගයක් පවතින විට එක් ද්රවස්තරයකින් අනෙක් ස්තරය මත සාපේක්ෂ ප්රවේගය වැළකෙන පරිදි බල ඇති වේ නම් එම බල දුස්ශ්රවී බල ලෙසද එවැනි තරල දුස්ශ්රාවී තරල ලෙස හැදින්වේ.
- යාබද තරල ස්ථර 2 ක් අතර සාපේක්ෂ චලිතයක් ඇති විට එය වැළකෙන පරිදි ස්පර්ශ පෘෂ්ටය දිගේ ප්රතිරෝද බල ක්රියා නොකරයි නම් එවැනි ප්රවාහයක් සුස්ස්රාවි තරල ලෙස හදුන්වයි. නමුත් මෙවැනි තරල ප්රායෝගිකව සොයාගත නොහැක.එනම් බොහෝ දුස්ස්රාවි බල ඉතා අඩු තරල මෙම ගතිගුණ පෙන්වයි.
අසම්පීඩ්ය තරල
- පීඩනය නිසා පරිමාවේ වෙනසක් සිදු නොවන ඕනෑම තරලයක් අසම්පීඩ්ය තරල ලෙස හදුන්වයි.
උදා : ද්රව අසම්පීඩ්ය වේ
සම්පීඩ්ය තරල
- පීඩනය මගින් පරිමාව වෙනස් කරගන්නා තරල සම්පීඩ්ය තරල වේ.
උදා : නිශ්චල වාතය සම්පීඩ්ය වේ
ප්රවාහ බටය
අනාකුල රේඛා සමූහයකින් සෑදෙන තරල කොටස ප්රවාහ බටය ලෙස හදුන්වයි.
සන්තත ප්රවාහ සමීකරණය
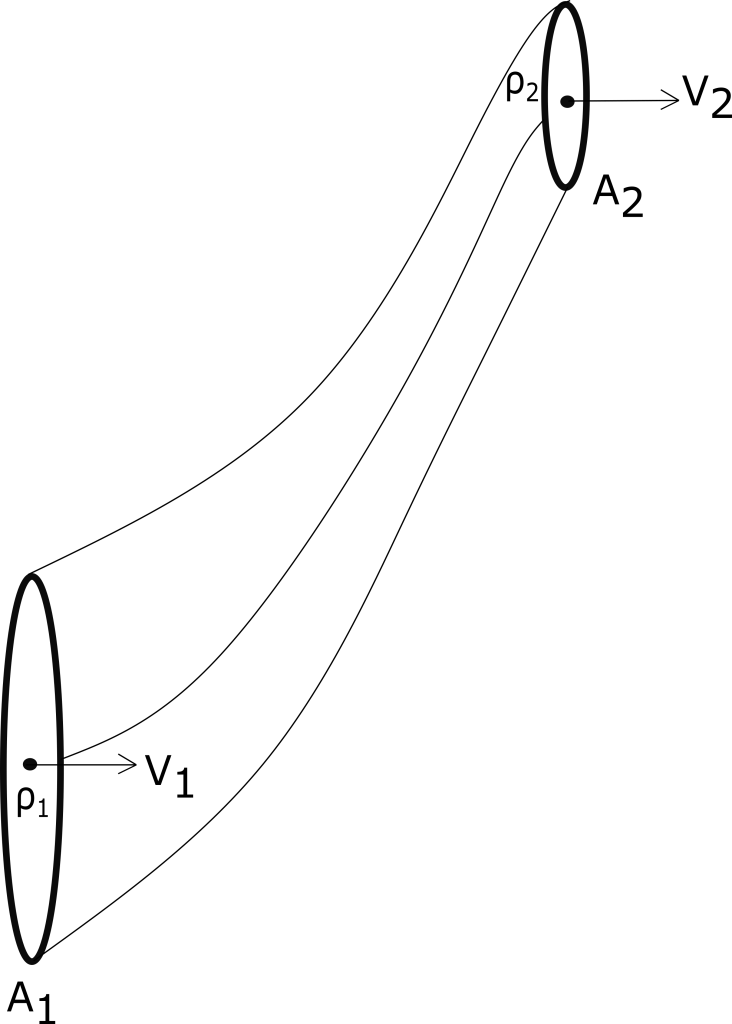
- ප්රවාහ බටයේ A ලක්ෂයේ හරස්කඩ වර්ගපලය A1 ද ද්රවයේ වේගය V1 ද ද්රවයේ ඝනත්වය ρ1 ද වේ. B ලක්ෂයේ හරස්කඩ වර්ගපලය A2 ද ද්රවයේ වේගය V2 ද ද්රවයේ ඝනත්වය ρ2 ද වේ.
- තත්පර 1 කදී A ලක්ෂය හරහා ඇතුළු වන ද්රව ස්කන්ධය = A1 V1 ρ1
- තත්පර 1 කදී B ලක්ෂය හරහා ඇතුළු වන ද්රව ස්කන්ධය = A2 V2 ρ2
- අනවරත ප්රවාහයක් බැවින් ,
- තත්පර 1 කදී A හරහා එකතුවන ද්රව ස්කන්ධය = තත්පර 1 කදී B හරහා එකතුවන ද්රව ස්කන්ධය
A1 V1 ρ1 = A2 V2 ρ2
- මෙය අසම්පිඩ්ය තරලයක් බැවින් ρ1 = ρ2
∴ A1 V1 = A2 V2
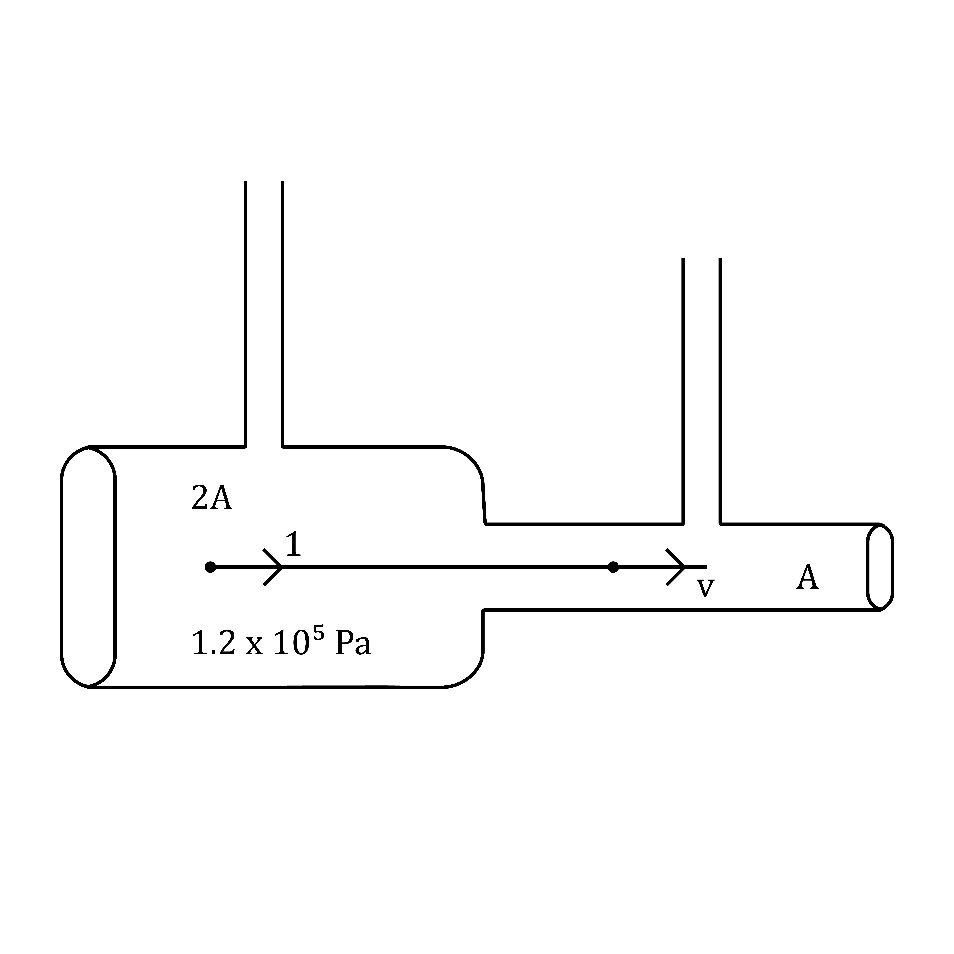
Q:හරස්කඩ වර්ගඵලය 2A වන නලයකට හරස්කඩ වර්ගඵලය A වන නලයක් සම්බන්ධ කර ඇත.විශාල නලයට 1 ms-1 ප්රවේගයෙන් ජලය ඇතුළු වේ. ජලය අසම්පීඩ්ය තරලයක් යයි සලකා සිහින් නලය තුල ද්රව ප්රවාහ වේගය ගණනය කරන්න.
A1 V1 = A2 V2
2A x 1 = A x v
v = 2 ms-1
බ’නුලි ප්රමේය
අසම්පිඩ්ය දුස්ශ්රවී බල නොසලකා හැරිය හැකි තරම් කුඩා වන තරලයක් අනාකුලව ප්රවාහය වන විට එහි ඕනෑම ලක්ෂයක පීඩනයේත්, ඒකක පරිමාවක චාලක ශක්තියේත් ඒකක පරිමාවක විභව ශක්තියේත් මුළු එකතුව නියතයක් වේ.
P + ½ρv2 + ρgh = k
P = පීඩනය
ρ = ඝනත්වය
v = ප්රවේගය
h = සම්මත මට්ටමක සිට උස
P = පීඩනය
½ρv2 = ඒකක පරිමාවක චාලක ශක්තිය
ρgh = ඒකක පරිමාවක විභව ශක්තිය
PA + ½ρvA2 + ρghA = PB + ½ρvB2 + ρghB
Q1 : වීදියේ මට්ටමේදී 3.8 atm පීඩනයකින් පවතින ජලය නලයක් හරහා 0.06 ms-1 වේගයෙන් ගොඩනැගිල්ලක් තුලට ගලයි. 20m ඉහලින් ඇති මහලක් තුලට එම නලය හරහා ජලය 2.2 ms-1 ප්රවේගයෙන් ගලයි නම් එවිට නලය තුල ජලයේ පීඩනය සොයන්න.
PA + ½ρvA2 + ρghA = PB + ½ρvB2 + ρghB
3.8x1x105 + ½ 1000x(0.06)2 + 0 = P + ½ 1000x(2.2)2 + 1000x10x20
P = 1.78 x 105 Pa
Q2: කට දක්වා පිරී ඇති ජාල බඳුනක් සලකන්න. එහි මුදුනේ සිට 20cm පහලින් සිදුරක් ඇත. ඉන් ජලය පිටවන ප්රවෙගය සොයන්න. මෙම බඳුන ඉතා විශාල යයි උපකල්පනය කරන්න.
බඳුන ඉතා විශාල බැවින් ජලය පිටවීමේදී කට අසලින් ජල මට්ටමේ පහල යෑම හෙවත් කට අසල ජලයේ ප්රවේගය නොසලකා හැරිය හැක. එහි චාලක ශක්තිය = 0 වේ. ඒ අසල වායුගෝලයට විවෘත බැවින් පීඩනය = වායුගෝලීය පීඩනය වේ. ජලය පිටවන සිදුර අසල ද වායුගෝලයට විවෘත බැවින් එහි පීඩනය ද වායුගෝලීය පීඩනය ට සමාන වේ.
PA + ½ρvA2 + ρghA = PB + ½ρvB2 + ρghB
1 atm + 0 + 1000x10x20x10-2 = 1 atm + ½ 1000xv2 + 0
2000 = 500v2
v2 = 4
v = 2ms-1
Q3: ජල බඳුනක් මත සිහින් බටයක් සිරස්ව පිහිටුවා බටයේ ඉහල කෙලවර හරහා වායු ප්රවාහයක් යැවේ. වායු ප්රවාහය තුල ජල අංශු තිබීමට වායු ප්රවාහයට තිබිය යුතු අවම ප්රවේගය සොයන්න. (වාතයේ ඝනත්වය = 1.2 kg m-3 සහ ජලයේ ඝනත්වය = 1000 kg m-3 වේ.)

- මෙහි අනාකුල රේඛා සමූහයකින් සෑදී ඇති මෙම තරල කොටසෙහි එනම් අනාකුල රේඛාව මත පිහිටි A හා B ලක්ෂ මත මත බ’නුලි ප්රමේය භාවිතා කල විට ඉහත සමීකරණය ලැබේ.
- මෙම තරල ප්රමාණය එකම තිරස් රේඛාවක ගලාගියේ නම්,
hA = hB = h
PA + ½ρvA2 + ρgh = PB + ½ρvB2 + ρgh
PA + ½ρvA2 = PB + ½ρvB2
Q: දුම්රිය වේදිකාවක් අසලින් දුම්රියක් යාමේදී 20 ms-1 ක ප්රවේගයෙන් චලිත වන වායු ප්රවාහයක් ඇතිවේ. වාතයේ ඝනත්වය 1.3 kg m-3 නම් වේදිකාව මත සිටින මිනිසෙකුගේ පීඩන වෙනස ක්රියා කරන වර්ගඵලය 0.4 m2 නම් මිනිසා මත ක්රියා කරන සම්ප්රයුක්ත බලය කොපමණද?

බ’නුලි ප්රමේය භාවිතා වන අවස්ථා
1.ගුවන් යානයක් ඉහල නැංවීමට බ’නුලි ප්රමේය භාවිත වේ.
- ගුවන් යානයක තටුවකට ඉහලින් හා පහලින් V1 හා V2 වේගයෙන් වාතය ගලායයි. තටුවේ වර්ගඵලය A නම් එය මත ඉහලට ඇතිවන බලය F නම්,
F = ½ ρ (v12 – v22) A වේ.
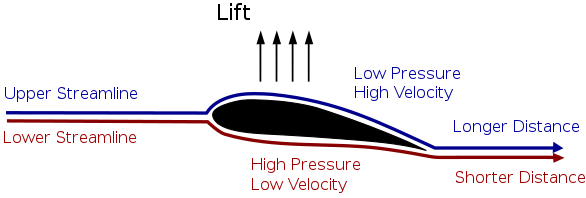
Q: ගුවන් යානයක් v වේගයකින් තිරස්ව පියාසර කරයි . ගුවන් යානයට සාපේක්ෂව ඉදිරියෙන් වායු ප්රවාහයක් ඇතිවේ.

- වායු ප්රවාහයේ ප්රවේගය සහ එහි දිශාව
- ගුවන් යානයට ඉදිරියේ A වර්ගඵලයක් ඇති වායු ප්රවාහයේ වර්ගඵලය ගුවන් යානයට ඉහලදී o.8 A තෙක් අඩු වේ නම් ගුවන් යානයට ඉහලින් වායු ප්රවාහ ප්රවේගය
- ගුවන් යානයේ ස්කන්ධය 6000 kg වන අතර වාතයේ ඝනත්වය 2 kg m-3වේ. පීඩන අන්තරය ක්රියා කරන වර්ගඵලය 20 m2 නම් ගුවන් යානය අහසේ රැඳී තිබීමට ගුවන් යානයට තිබිය යුතු අවම ප්රවේගය සොයන්න.
පිළිතුරු:
1.වායු ප්රවාහයේ ප්රවේගය = ගුවන් යානයේ චලිත දිශාවට විරුද්ධ දිශාවට v
2.
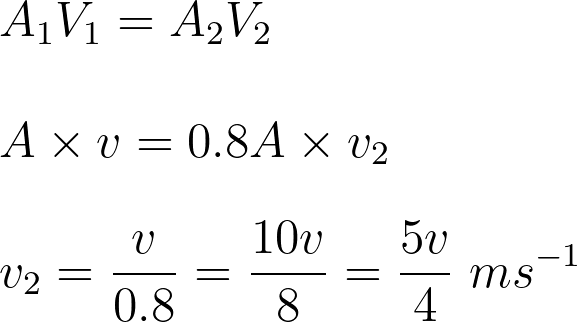
3.
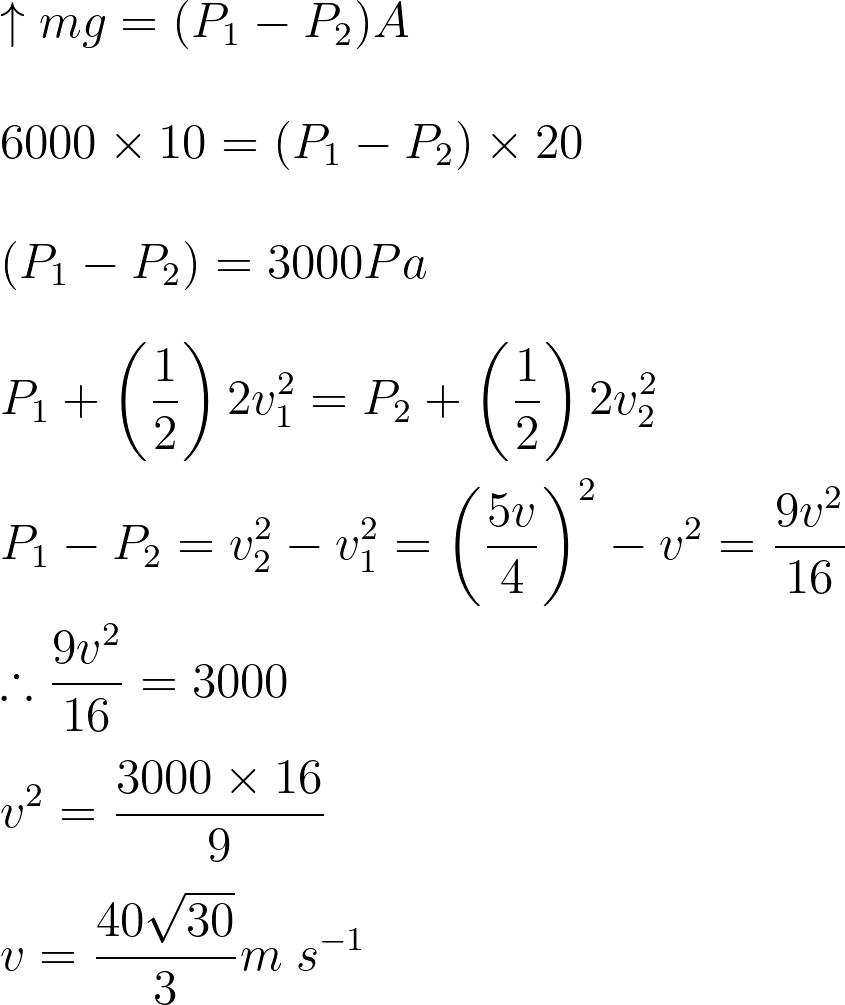
2. ක්රිකට් ක්රීඩාවේදී පන්දු යැවීම සඳහා බ’නුලි ප්රමේය
- පන්දුවක් වේගයෙන් ඉදිරියට ගමන් කරන විට පන්දුවට සාපේක්ෂව වාතයේ අනාකුල රේඛා පන්දුවේ දෙපසින් සමමිතිකව ගලා යයි. එම නිසා ඉන් විශේෂිත බලපෑමක් ඇති නොවේ.
- නමුත් වේගයෙන් පන්දු යවන්නා සෑම විටම පන්දුවේ එක් අර්ධයක් හොදින් පිරිමදිනු ලැබේ. එවිට එක් අර්ධයක් සුමට වන අතර අනෙක් අර්ධය ඊට සාපේක්ෂව රළු වේ.
- පන්දුව වේගයෙන් ඉදිරියට ගමන් කරන විට සුමට පැත්තේ ගලායන වාත අංශු එයට ආකර්ෂණය නොවී ලිස්සා යන බැවින් අනාකුල ලේඛා ලං වීමක් සිදු නොවේ. රළු පැත්තෙන් ගලා යන විට රේඛා ලංවේ. වාත අංශු වල ප්රවේගය වැඩි වේ. බ’නුලි ප්රමේයට අනුව පීඩනය අඩු වේ.
- එවිට සුමට පැත්තේ සිට රළු පැත්තට පීඩන වෙනසක් ඇතිවේ. එබැවින් බලයක් හට ගනී. එවිට පන්දුව තාම ගමන් මාර්ගය වෙනස් කරගනි. එනම් දෝලනය වේ. පන්දුව විකට්ටුව දෙසට දෝලනය වුවත් ඉවතට දෝලනය වුවත් පිතිකරුවා දවා ගැනීම පහසු වේ.
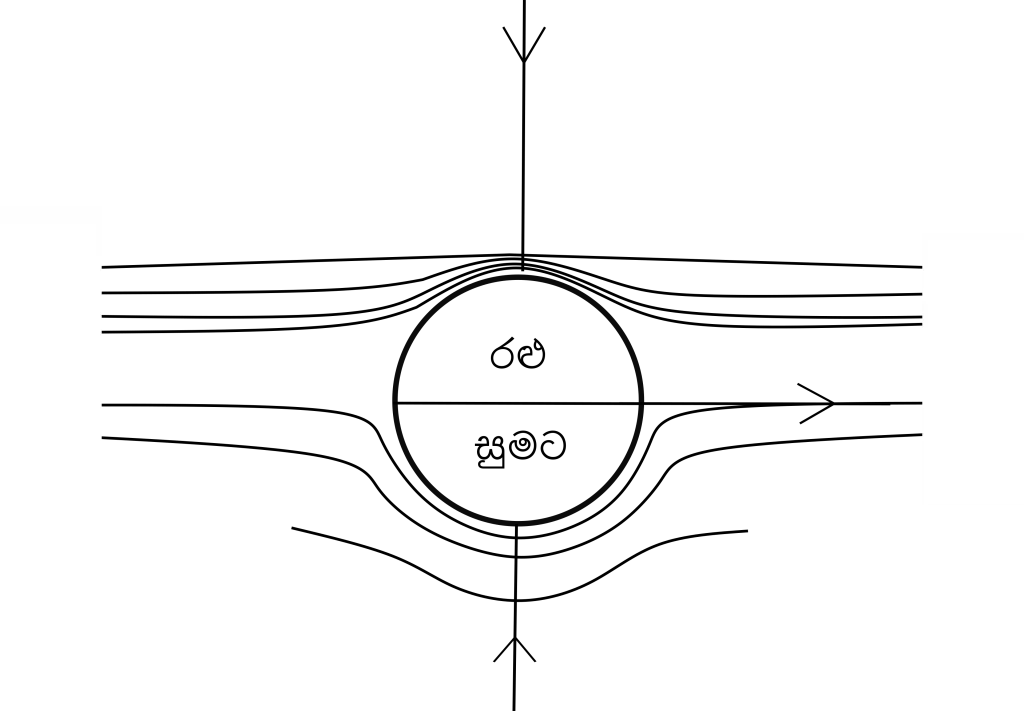
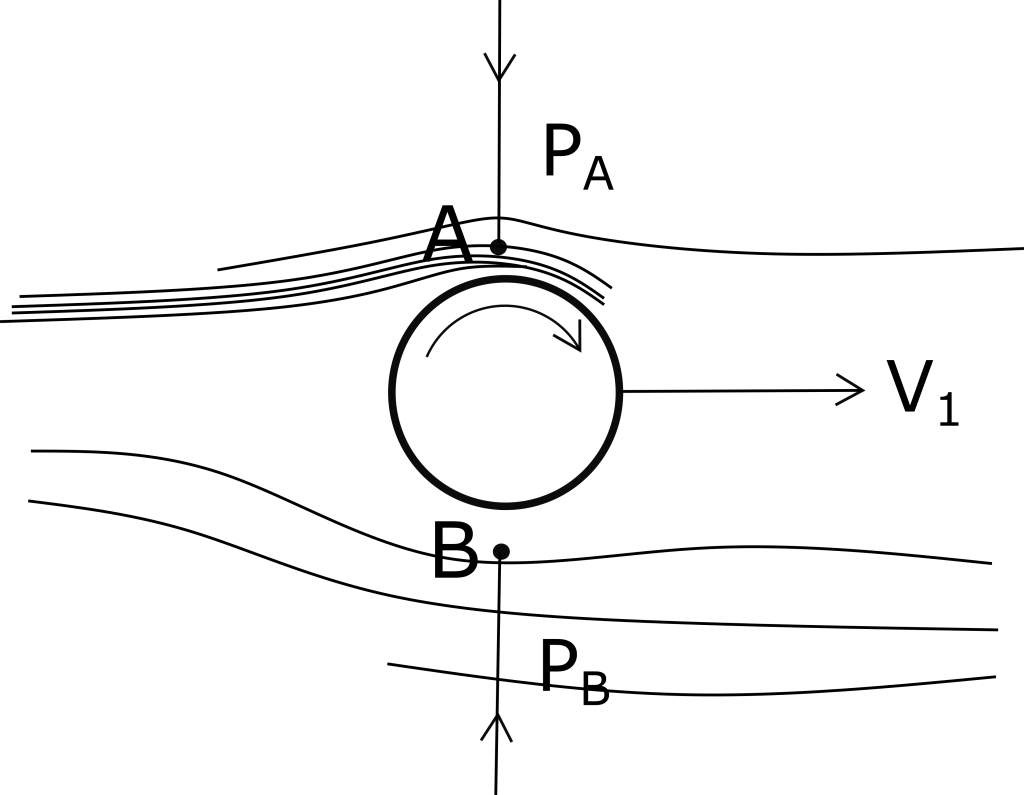
- දඟ පන්දු යවන්නෙකුද පන්දුව දෝලනය කිරීමට පන්දුව හැකි තරම් දොලනය් කරවයි. ඉහත රුපයේ දැක්වෙන පරිදි පන්දුව දක්ෂිණාවර්ත දිශාවට භ්රමණය වෙමින් ඉදිරියට ගමන් කරයි නම් එ පැත්තෙන් වේගය වැඩි වීම නිසා අනාකුල රේඛා ලංවීම සිදුවේ. පීඩනය අඩුවේ.
- B පැත්තේ වේගය එසේ වැඩි නොවන නිසා අනාකුල රේඛා ලං නොවේ. පීඩනය අඩු නොවේ. මේ නිසා B පැත්තේ සිට A පැත්තට පීඩන අන්තරයක් හට ගනී. එම නිසා බලයක් හට ගනී.
- පන්දුව තණතිල්ලේ ගැටී නැවත එක්වරම තාම දිශාව වෙනස් කරගනී.එවිට පිතිකරු දවා ගැනීම පහසු වේ.
3. බන්සන් දාහකයේ ක්රියාව.
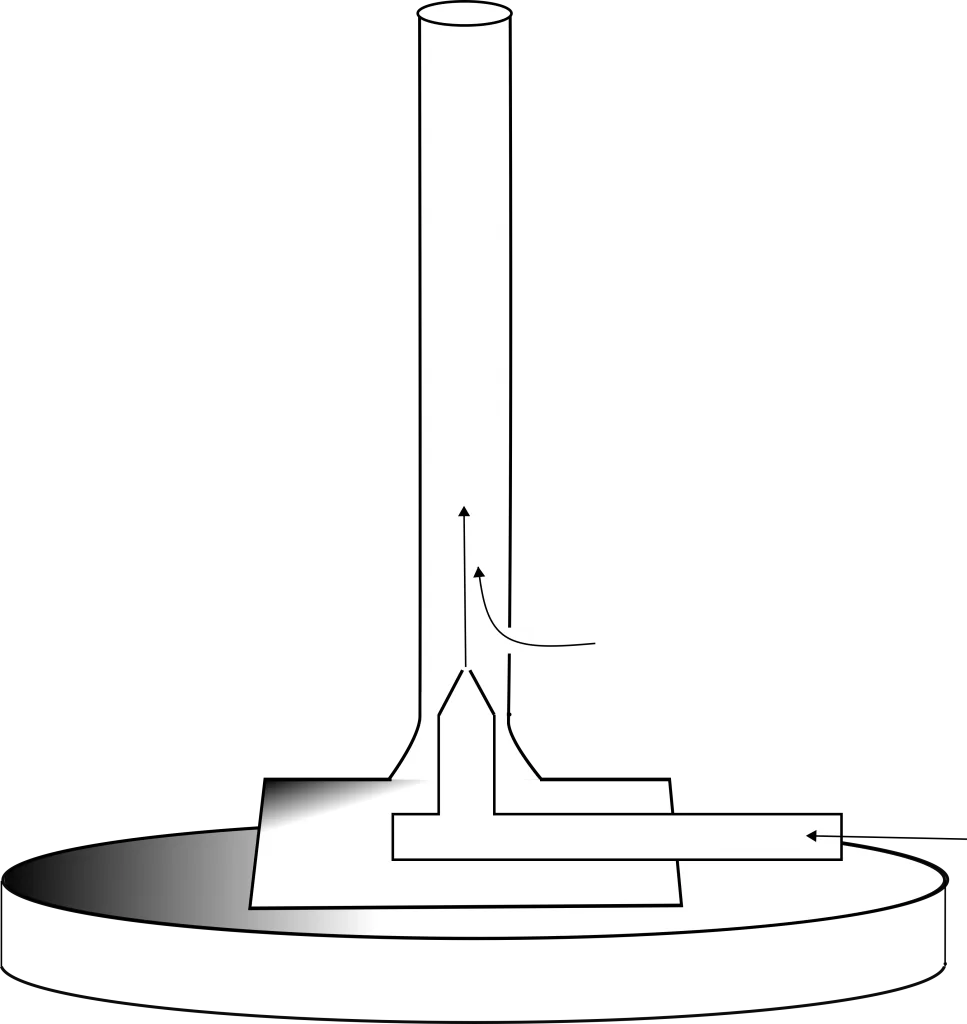
- බන්සන් දාහකයේ ඉන්ධන ගලායන නලය තුලින් ඇතුලට ඉන්ධන ගලා ආ විට එය කුඩා විවරයක් තුලින් ඉන්ධන පිටවන විට අනාකුල රේඛා ලං වන බැවින් වේගය වැඩිවේ. පීඩනය අඩුවේ.
- එවිට වායුගෝලයේ ඇති වාතය අඩු පීඩනය ඇති දෙසට ගලායන නිසා ඉන්ධන දහනයට අවශ්ය O2 ප්රමාණවත් ලෙස ලැබී පුර්ණ දහනයට ලක්වේ.>
4. උමං ජල මාර්ග වල ක්රියාව
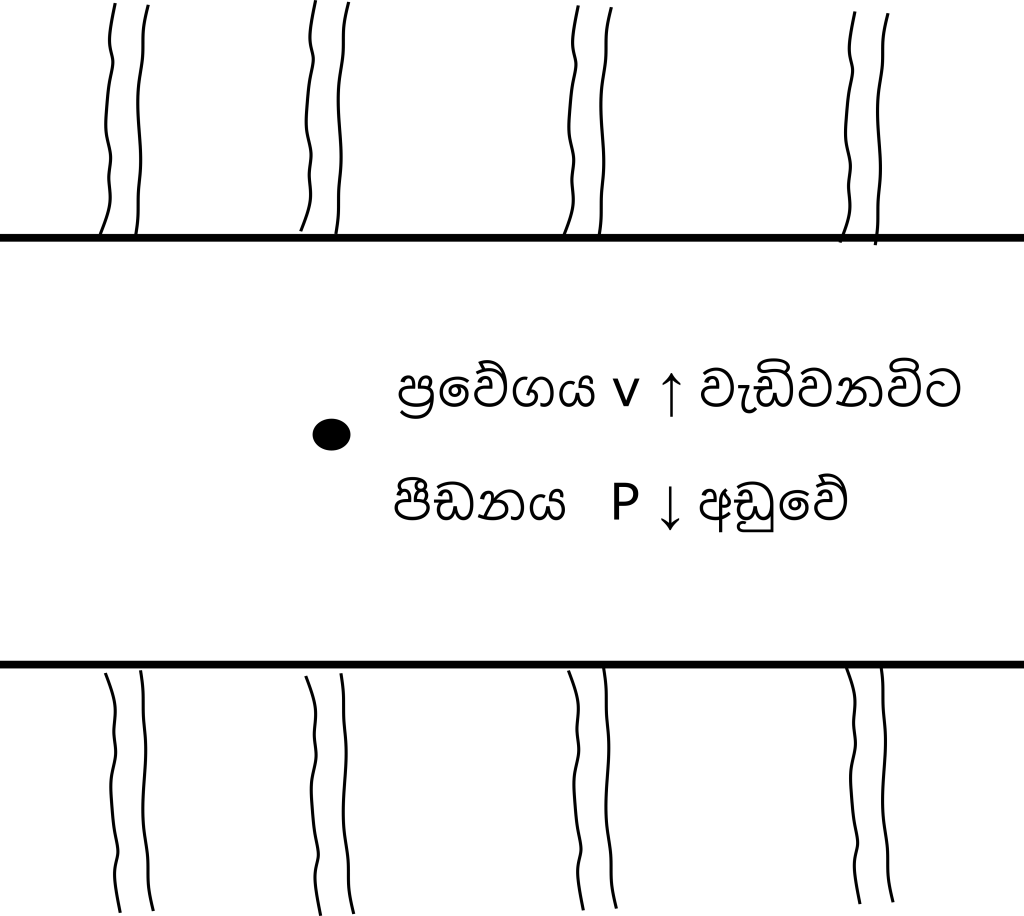
- පොලව යටින් උමං කපා ජලය ගෙනයාමේදී ජලය උමග තුලින් වේගයෙන් ගලයනවිට බ’නුලි ප්රමේයට අනුව පීඩනය අඩුවේ. එවිට උමගට සම්බන්ධව ඇති උල්පත්වල ජලය අඩු පීඩනය ඇති දෙසට ගලායයි.
- එවිට ටික කාලයකට පසු අවට ඉඩම් වල ඇති උල්පත් ජලය සම්පුර්ණයෙන්ම සිඳී යයි. ඒවා මුඩු ඉඩම් බවට පත්වේ.
5. සත්ව ගුල්
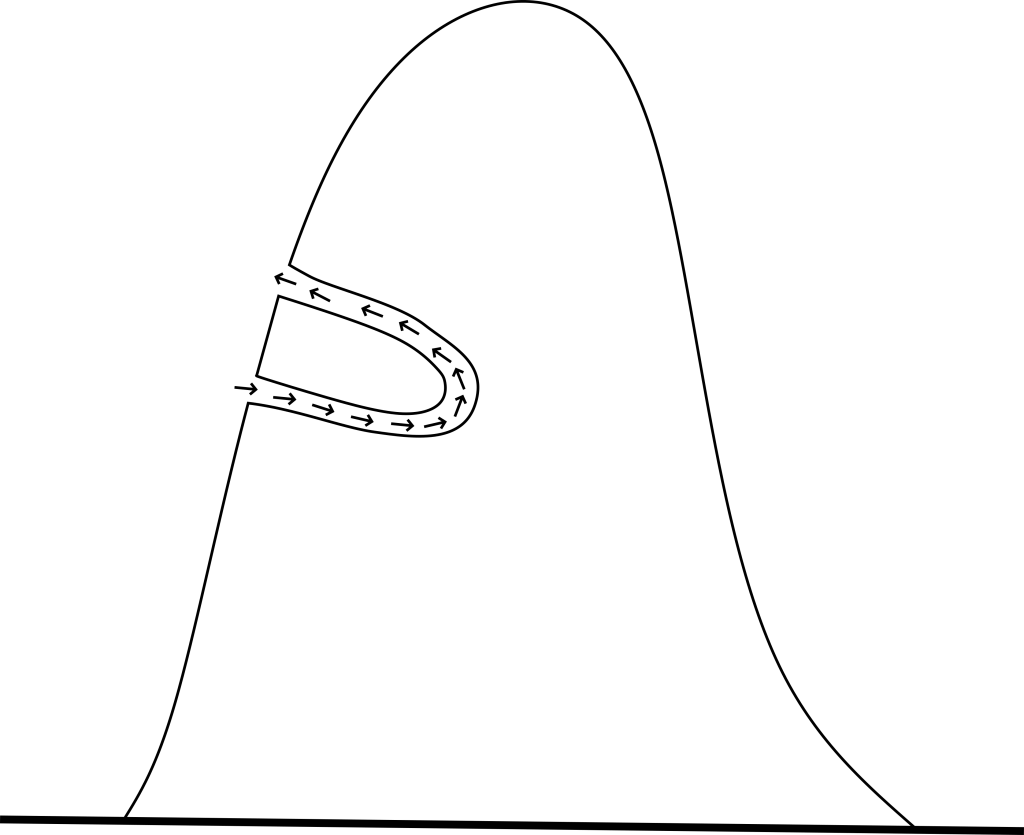
- පොලව යට ගුල් සාදාගෙන ජීවත් වන සතුන් එම ගුල සාදාගනු ලබන්නේ එක් කෙළවරක් පහත් මට්ටමක හා අනෙක් කෙලවර සාපේක්ෂව ඉහලින් තිබෙන පරිදිය.
- බොහෝවිට ඉහලින් යන වාතයේ වේගය වැඩි බැවින් බ’නුලි ප්රවේගයට අනුව පීඩනය අඩුවේ. නමුත් ගුලෙහි පහල කෙලවර එලෙස පීඩන අඩුවීමක් සිදු නොවෙන බැවින් පහල කලාපයේ කෙලවරින් වාතය ගුල තුලට ඇතුල්වී පීඩනය අඩු කෙලවර දෙසට ගලා යයි. එවිට ගුල තුල සිටින සතුන්ට අවශ්ය වාතය ප්රමාණවත් ලෙස ලැබේ.
6. පින් පොන්ග් බෝලය
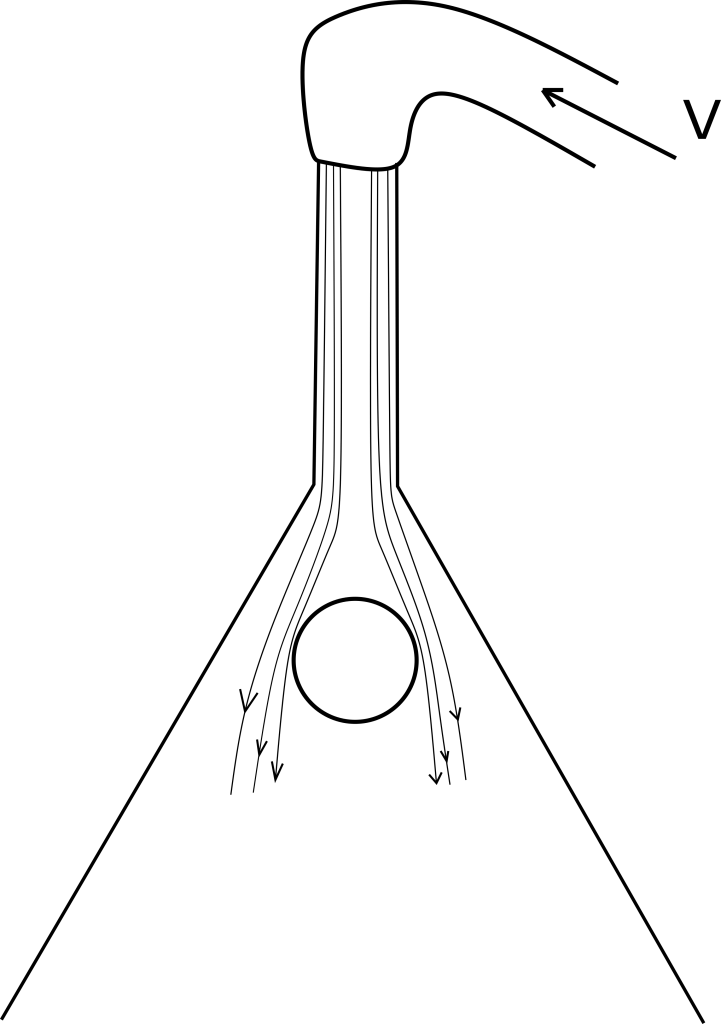
- පුනීලයක් යටිකුරු කර තබා එහි ඉහලින් අධික වේගයෙන් වාතය ඇතුළු කර පහල කෙලවරින් පිටව යාමට සලස්වයි. සැහැල්ලු කුඩා බෝලයක් ගෙන පුනීලය තුල තබා අතහැරි විට එය පහලට නොවැටී පවතී.
- එයට හේතුව බෝලයට ඉහලින් ඇති වාතයේ අනාකුල රේඛා ලංවේ. එවිට ප්රවේගය වැඩිවෙයි. පීඩනය අඩුවේ. නමුත් බෝලයට පහලින් වාතයේ ප්රවේගය අඩුය. පීඩනය වැඩිවේ. මේ නිසා බෝලය මත පීඩන අන්තරයක් ඇතිවේ.
- එමගින් බලයක් ඇතිවේ. එය බෝලයේ බරට වඩා වැඩි බැවින් පහලට නොවැටී පවතී.
ඔබට මෙම කොටස වීඩියෝ මගින් අධ්යයනය කිරීමට :
මෙම වීඩියෝවේ
- ආකූල හා අනාකූල ප්ර්වාහ
- සාත්න්ය් ප්ර්වාහ සමීකරනය
- බර්නූලි මූලදර්මය
යන කරුණු අඩංගු වේ.
මෙම වීඩියෝවේ
- බර්නූලි මූලධර්මයේ යෙදීම අඩංගු වේ.

