වෘත්තයක් හා සරල රේඛාවක් ජේදනය වන විට ජේදන ලක්ෂ්ය හරහා ඇදිය හැකි ඕනෑම වෘත්තයක සාධාරණ ආකාරය
- S=x2+y2+2gx+2fy+c =0 හා u= lx+my+n =0 වෘත්තය සලකමු.
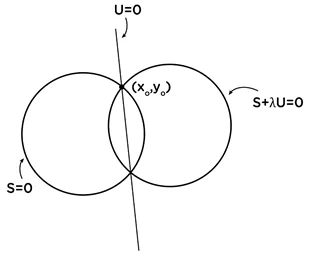
- වෘත්තයේ හා සරල රේඛා දෙකෙන් ඕනෑම ජේදන ලක්ෂයක් (x0 ,y0) යැයි ගනිමු .මෙම (x0 , y0) මගින් වෘත්තයේ හා සරල රේඛාවේ සමීකරණ තෘප්ත වේ.
මෙහි x2,y2 පද පවතින අතර ඒවායේ λ හි දෙන අගයක් සදහා ඉහත A මගින් වෘත්තයක සමීකරණයක්ද , λ හි වෙනස් අගයක් සදහා A මගින් වෘත්ත පන්තියක්ද නිරූපණය වේ .
(x0, y0) ලක්ෂ්යයේ ඛණ්ඩාoක ඉහත A හි වම්පස ආදේශ කරමු.
\begin{array}{rcl}\text{වම් පැත්ත}&=&x_0^2+y_0^2+(2g+\lambda l)x_0+(2f+\lambda m)y_0+(c+\lambda n)\\&=&(x_0^2+y_0^2+2gx_0+2fy_0+c)+\lambda(lx_0+my_0+n)\\&=&\text{දකුණු පැත්ත}\end{array}(x0 ,y0) මගින් ඉහත A ගෙන් දැක්වෙන වෘත්ත සමීකරණ තෘප්ත වේ . එම නිසා ඉහත A ගෙන් නිරූපණය වන සියලුම වෘත්ත (x 0 , y 0 ) ලක්ෂ්යය හරහා යයි.
- S =0 යනු වෘත්තයේ u=0 සරල රේඛාවෙන් ජේදන ලක්ෂ්යය හරහා යන ඕනෑම වෘත්තයක සාධාරණ සමීකරණය s+λu =0 ආකාරය වේ. මෙහි λ යනු x හා y ගෙන් ස්වායත්ත විචල්යය පරාමිතියකි .
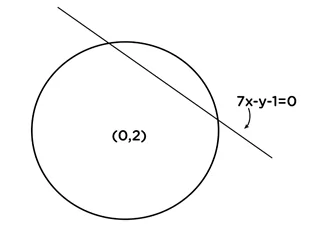
l=0 හා s=0 හි ජේදන ලක්ෂ්යය හරහා යන ඕනෑම වෘත්තයක සමීකරණය s +λl =0 ආකාර වේ.
\begin{array}{l}(3x^2+3y^2-4y–\frac34)+\lambda(7x-y-1)=0\;\rightarrow\ast\\\text{(0,0 ) හරහා යන බැවින්}\;\ast\;\text{මගින් (0,0) ලක්ෂ්යය තෘප්ත කරයි .}\\-\lambda-\frac34=0\\\lambda=-\frac34\end{array}අවශ්යය වෘත්තයේ සමීකරණය ,
\begin{array}{rcl}(3x^2+3y^2-4y–\frac34)-\frac34(7x–y–1)&=&0\\12x^2+12y^2-13y-21x&=&0\end{array}වෘත්තයක් මගින් තවත් වෘත්තයක පරිධිය සමච්ජේද කිරීමේ අවශ්යතාවය.
- S≡ x2+y2+2gx+2fy+c=0 වෘත්තය මගින්, S’≡ x2+y2+2g ’x+2f ’y+c=0 වෘත්තයේ පරිධිය ඡේදනය කරන බව සිතමු.
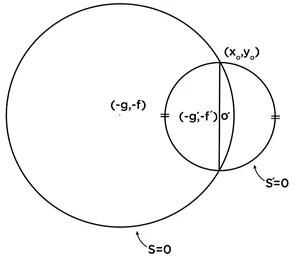
S=0 හා S’=0 වෘත්ත දෙකේ ජේදන ලක්ෂ්ය දෙකෙන් ඕනෑම ජේදන ලක්ෂ්යයක් (x0,y0) මගින් ඉහත වෘත්ත දෙකේ සමීකරණයන් තෘප්ත කෙරේ.
\begin{array}{l}S\equiv x^2+y^2+2gx+2fy+c=0\;\rightarrow①\;\\S^/\equiv x^2+y^2+2g^/x+2f^/y+c=0\rightarrow②\\①-②\\2(g-g^/)x_0+2(f-f^/)y_0+(c-c^/)=0\;\text{ලෙස ලැබේ.}\end{array}මෙයින් පැහැදිලි වන්නේ (x0 , y0) මගින්, 2(g-g’) x0 +2(f-f’)y0 +(c-c’) = 0 සරල රේඛාවේ සමීකරණය තෘප්ත වී ඇති බවය.
∴ 2(g-g’) x0 +2(f-f ’)y0 +(c-c’) = 0 සරල රේඛාව වෘත්ත දෙකේ ජේදන ලක්ෂ්ය හරහා යන අතර මෙම රේඛාව S=0 හා S’=0 වෘත්ත දෙකේ පොදු ජ්යාය වේ.
- S=0 වෘත්තය මගින් S’=0 වෘත්තයේ පරිධිය සමච්ජේද කරයි නම්, පොදු ජ්යාය S’=0 වෘත්තයේ විෂ්කම්භය වේ. එම නිසා S’=0 වෘත්තයේ කේන්ද්රය වන O’≡(-g ,-f) මගින් ඉහත පොදු ජ්යායේ සමීකරණය තෘප්ත කෙරේ.
S=0 වෘත්තය මගින් S’=0 වෘත්තයේ පරිධිය සමච්ජේද වන විට,
\begin{array}{rcl}2(g-g^/)(-g^/)+2(f-f^/)(-f^/)+(c-c^/)&=&0\\2(g^/)^2+2(f^/)^2-c^/&=&2gg^/+2ff^/-c\;\text{ලෙස ලැබේ.}\end{array}2(g’)2 +2(f ’)2 -c’ = 2gg’+2ff ’ – c යන්න S=0 මගින් S’=0 වෘත්තයහි පරිධිය සමච්ජේද කිරීම සදහා අවශ්යතාවය වේ.
උදා :(1.) x2+y2+ 2y=3 වෘත්තයේ පරිධිය සමච්ජේද කරමින් මූල ලක්ෂ්යයේදී x-y=0 රේඛාව ස්පර්ශ කරන වෘත්තයේ සමීකරණය සොයන්න.
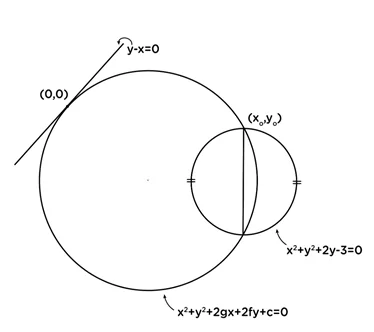
අවශ්ය වෘත්තය x2+y2+2gx+2fy+c=0 යැයි ගනිමු.
වෘත්ත දෙකේ ඕනෑම ජේදන ලක්ෂ්යයේ (x0 ,y0 ) ලෙස ගනිමු. මෙවිට මෙම ඛණ්ඩාංකය මගින් ඉහත වෘත්ත සමීකරණ 2 ම තෘප්ත කෙරේ.
\begin{array}{rcl}x_0^2+y_0^2+2y_0-3&=&0-①\\x_0^2+y_0^2+2gx_0+2fy_0+c&=&0-②\\①-②\;\text{න්}&=&\\2gx_0+2(f-1)y_0+c+3&=&0\\2gx\;+2(f-1)\;y\;+c\;+\;3&=&0\;\text{සරලරේඛාව }(x_0,y_0)\;\text{මගින් තෘප්තවේ}\\\therefore2gx\;+\;2(f-1)\;y\;+c\;+\;3\;\;\;&=&0\;\text{සරල රේඛාව වෘත්ත දෙකේ පොදු ජ්යායේ සමීකරණය වේ. }\\&&\end{array}x2+y2+2gx+2fy+c=0 වෘත්තයේ පරිධිය සමච්ජේද වන නිසා පොදු ජ්යාය මෙම වෘත්තයේ විෂ්කම්භයකි. එම නිසා x2 +y2+ 2y -3 = 0 වෘත්තයේ කේන්ද්රය මගින් පොදු ජ්යායේ සමීකරණය තෘප්ත වේ.
x2 +y2+ 2(-1) y -3 = 0 , වෘත්තයේ කේන්ද්රය ≡ (0, -1)
\begin{array}{rcl}2g(0)+2(f-1)\;(-1)+c+3&=&0\\2-2f+c+3&=&0\\c-2\;f&=&-5\;\rightarrow\;③\end{array}අවශ්ය වෘත්තය මූල ලක්ෂ්ය හරහා යන බැවින් c=0 ක් වේ.
\begin{array}{rcl}③\;\;\text{ට අනුව}\;,\;0-2f&=&-5\\f&=&\frac52\end{array} \begin{array}{rcl}\text{x-y=0}\;\text{රේඛාවේ අනුක්රමණය}&=&1\\(0,0)\text{ලක්ෂ්යයේ දී වෘත්තයේ අනුක්රමණය}&=&\left(\frac{dy}{dx}\right)(0,0)\\x^2+y^2+2gx+2fy+c&=&0\\2x+2y\left(\frac{dy}{dx}\right)+2g+2f\left(\frac{dy}{dx}\right)&=&0\\\left(\frac{dy}{dx}\right)&=&-\frac{(x+g)}{(f+y)}\\\left(\frac{dy}{dx}\right)(0,0)&=&-\frac gf\end{array} \begin{array}{rcl}{\left(\frac{\operatorname dy}{\operatorname dx}\right)}_{\left(\left(0,0\right)\right)}&=&\left(0,0\right)\;\text{ලක්ෂ්යයේදී වෘත්තයට ඇදි ස්පර්ශකය අනුක්රමණය වන y-x=0 රේඛාවේ අනුක්රමණය}\\&=&1\\-\frac gf&=&1\\g&=&-f\\g&=&-\frac52\end{array}අවශ්ය වෘත්තයේ සමීකරණය,
\begin{array}{rcl}x^2+y^2+2\left(-\frac52\right)x+2\left(\frac52\right)y+0&=&0\\x^2+y^2-5x+5y&=&0\end{array}උදා : (2.) x 2+ y2 -6x +2y -17 =0 සහ x-y+2=0 සරල රේඛාව A සහ B ලක්ෂ්ය වලදී එකිනෙක ජේදනය කරයි.AB විෂ්කම්භය ලෙස ඇති වෘත්තයේ සමීකරණය සොයන්න.A සහා B හරහා යන වෘත්තයේ සමීකරණය,(වෘත්තයක් සහ සරල රේඛාවක ජේදන ලක්ෂ්ය හරහා යන වෘත්තයක සමීකරණය S+λU සාදාරන ආකාරයෙන් ඉදිරිපත් කල හැක.)
\begin{array}{rcl}x^2+y^2-6x+2y-17+\lambda\left(x-y+2\right)&=&0\\x^2+y^2–(6-\lambda)x+(2-\lambda)y-17+2\lambda&=&0\\x^2+y^2+2\left[-\frac{\left(6-\lambda\right)}2\right]x+2\left[\frac{(2-\lambda)}2\right]y-17+2\lambda&=&0\\\text{මෙම වෘත්තයේ කේන්ද්රය}&=&\left(\left(3-\frac\lambda2\right),\left(\frac\lambda2-1\right)\right)\end{array}AB විෂ්කම්භයක් වන නිසා කේන්ද්රයේ ඛණ්ඩාංක මගින් සරල රේඛාවේ සමීකරණය තෘප්ත වේ.
\begin{array}{rcl}\left(3-\frac\lambda2\right)-\left(\frac\lambda2-1\right)+2&=&0\\\lambda&=&6\end{array}AB විෂ්කම්භයක් වශයෙන් ඇති වෘත්තයේ සමීකරණය,
\begin{array}{rcl}x^2+y^2-6x+2y-17+\lambda(x-y+2)&=&0\\x^2+y^2-4y-5&=&0\end{array}වෘත්ත දෙකක් ප්රලම්භව ජේදනය වීමේ අවශ්යතාවය.
- ජේදනය වන වෘත්ත යුගලක ඕනෑම ජේදන ලක්ෂ්යයකදී වෘත්තදෙකට අදින ලද ස්පර්ශක එකිනෙකට ලම්භක නම් එම වෘත්ත ප්රලම්භව ජේදනය වන්නේ යැයි කියනු ලැබේ.
- S1≡ x2+y2+2g1x +2f1y+c1 =0 හා S2≡ x2+y2+2g2x +2f2y+c2=0 වෘත්ත ප්රලම්භව ජේදනය වන්නේ යැයි සිතමු.
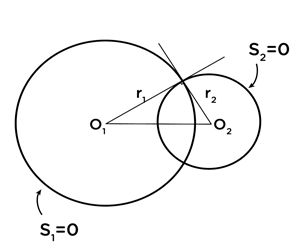
වෘත්ත දෙක ප්රලම්භව ජේදනය වන නිසා O1PO2 ඍජුකෝණික ත්රිකෝණයකි.මෙය සදහා පයිතගරස් ප්රමේය යෙදීමෙන්,
\begin{array}{rcl}O_1O_2^2&=&r_1^2+r_2^2\\\left(g_2-g_1\right)^2+\left(f_2-f_1\right)^2&=&(g_1^2+f_1^2-c_1)+(g_2^2+f_2^2-c_2)\\2g_1g_2+2f_1f_2&=&c_1+c_2\end{array}- 2g1g2+2 f1f2=c1+c2 , S1=0 හා S2=0 වෘත්ත ප්රලම්භව ජේදනය වීමේ අවශ්යතාවය වේ.
උද: (1.) x2+y2 =1 වෘත්තයේ පරිධිය සමච්චේද කරමින්ද, x2+y2-4y-5=0 වෘත්තය ප්රලම්භව සමච්ජේද කරමින්ද, (2,0) ලක්ෂ්ය හරහා යමින්ද පවතින වෘත්තයේ සමීකරණය සොයන්න.
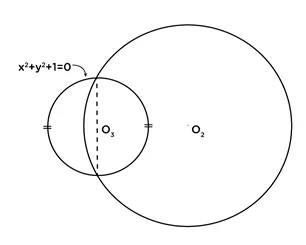
අවශ්ය වෘත්තයේ සමීකරණය ,
S≡ x2+y2+2gx+2fy+c=0 යැයි ගනිමු.
x2+y2 =1 සහ S=0 වෘත්තයන්හි ජේදන ලක්ෂ්ය දෙකෙන් ඕනෑම එකක් (x0, y0) යැයි ගනිමු. (x0 , y0) මගින් ඉහත වෘත්ත සමීකරණ දෙකම තෘප්ත වේ.
\begin{array}{rcl}x_0^2+y_0^2&=&1-①\\x_0^2+y_0^2+2gx_0+2fy_0+c&=&0-②\end{array} \begin{array}{rcl}&&①-②\;\text{න්,}\end{array} \begin{array}{rcl}2gx_0+2fy_0+c+1&=&0\\(x_0,y_0)\;\text{මගින් }2gx+2fy+c+1&=&0\;\text{සරල රේඛාවේ සමීකරණය තෘප්ත වී ඇත.}\end{array}වෘත්ත දෙකේ ජේදන ලක්ෂ්ය හරහා යන සරල රේඛාව වූ 2gx+2fy+c+1=0 , x2+y2=1 සහ S=0 වෘත්තයන්හි පොදු ජ්යායේ සමීකරණය වේ.
x2+y2 =1 වෘත්තයේ පරිධිය S=0 වෘත්තය මගින් සමච්ජේද කර ඇති නිසා ඉහත පොදු ජ්යාය x2+y2 =1 වෘත්තයේ විෂ්කම්භයකි.
x2+y2 =1 වෘත්තයේ කේන්ද්රයේ ඛණ්ඩාංක=(0,0)
(0,0) මගින් ඉහත පොදු ජ්යායේ සමීකරණය තෘප්ත කෙරේ.
\begin{array}{rcl}c+1&=&0\\c&=&-1\end{array}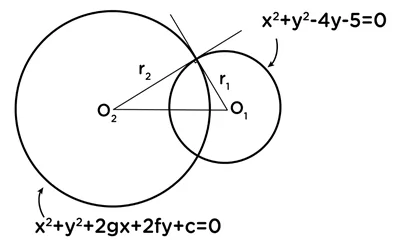
1 ක්රමය
\begin{array}{rcl}x^2+y^2-4\text{y-5=0}\;\text{වෘත්තයේ කේන්ද්රය }O_1&=&(0,2)\\\text{අරය }r_1&=&\sqrt{({0^2+2^2-(-5)}}\\&=&3\\x^2+y^2+\text{2gx+2fy+c=0වෘත්තයේ කේන්ද්රය}&=&(-g,-f)\\\text{අරය }r_2&=&(g^2+f^2-c)\\&=&\sqrt{g^2+f^2-(-1)}\\O_1O_2&=&\sqrt{(0+g)^2+(2+f)^2}\end{array}වෘත්ත දෙක ප්රලම්භ සමච්ජේද වන නිසා,
\begin{array}{rcl}r_1^2+r_2^2&=&(O_1O_2)^2\\3^2+(g^2+f^2+1)&=&g^2+f^2+4+4f\\f&=&\frac32\end{array}2 ක්රමය
වෘත්ත දෙකක් ප්රලම්භව සමච්ජේද වීමේ අවශ්යතාවය නිරූපණය වන ප්රකාශනය භාවිතා කිරීමෙන්ද මෙම ගැටලුව විසදිය හැක.
වෘත්ත දෙකක් ප්රලම්භව සමච්ජේද වීමේ අවශ්යතාවය ඇසුරින්,
\begin{array}{rcl}2g_1g_2+2f_1f_2&=&c_1+c_2\\2(g)(0)+2(f)(2)&=&-5+(-1)\\f&=&\frac32\end{array}තවද වෘත්තය (2,0) ලක්ෂ්යය හරහා යන නිසා එම ලක්ෂ්යයේ ඛණ්ඩාංක මගින් වෘත්ත සමීකරණ තෘප්ත වේ.
\begin{array}{rcl}0^2+2^2+2g(2)+2f(0)&=&0\\4+4g+c&=&0\\g&=&-\frac34\;(c=-1\text{නිසා})\end{array}අවශ්ය වෘත්තයේ සමීකරණය,
\begin{array}{rcl}x^2+y^2+2\left(-\frac34\right)x+2\left(\frac32\right)y-1&=&0\\x^2+y^2-\frac32x+3y-1&=&0\\2x^2+2y^2-3x+6y-2&=&0\end{array}උදා: (3.) (0,3 ) ලක්ෂ්යයේදී y අක්ෂය ස්පර්ශ කරන්න වූ ද, x2+y2 -8x +4y-5=0 වෘත්තය ප්රලම්භව ලෙස ජේදනය කරන්න වූ වෘත්තයේ සමීකරණය සොයන්න. [2014 A/L- part A (09)]
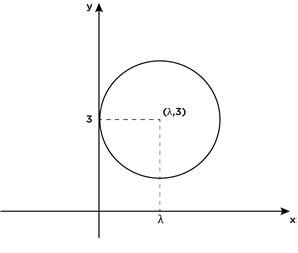
මෙය x2+y2 -8x+4y-5=0 වෘත්තයට ප්රලම්භ බැවින්,
වෘත්ත දෙක ප්රලම්භ ලෙස සමච්ජේදනය වීමේ අවශ්යතාව අනුව (2g1g2+2 f1f2= c1+c2),
\begin{array}{rcl}2(-4)(\lambda)+2(2)(-3)&=&-5+\;9\;\;\;\;\;⑤\\-8\lambda-12&=&4\\\lambda&=&2\;\;\;\;\;\;\;\;⑤\\\text{එනයින් අවශ්ය වෘත්තයේ සමීකරණය},\;x^2+y^2-4x-6y+9&=&0\;\text{වේ.}\;\;\;\;⑤\end{array}උදා : (4.) AB විෂ්කම්භය සහිත වෘත්තයේ සමීකරණය සොයන්න. මෙහි A ≡( 1, 3) හා B ≡ (2,4) වේ. තවද S වෘත්තය ප්රලම්භ ලෙස කපන (-1 , 2) කේන්ද්රය සහිත වෘත්තයේ සමීකරණය සොයන්න. [2012 A/L – part A(09)]
S වෘත්තය මත ඕනෑම ලක්ෂ්යයක් (x , y) යැයි ගනිමු.
\begin{array}{rcl}\text{එවිට}\;\left(\frac{(y-3)}{(x-1)}\right).\left(\frac{(y-4)}{(x-2)}\right)&=&-1\;\text{යැයි ලැබේ. }\boxed{10}\\\text{එනම් }x^2+y^2-3x-7y+14&=&0\;\text{වේ. ➄}\end{array}————————————————————————————————————————
වෙනත් ක්රමයක් ,
S වෘත්තයේ කේන්ද්රය (-g,-f) යැයි ගනිමු.
\begin{array}{rcl}\text{එවිට}-g&=&\frac{(2\;+1\;)}2=\frac32\\-f&=&\frac{(3+\;4)}2=\frac72\;\text{යැයි ලැබේ.}\;\;\;➄\\&&\text{S වෘත්තයේ අරය=}\frac{\sqrt{(2-1)^2+(4-3)^2}}2=\frac{\sqrt2}2\;\;\;➄\\&&\end{array} \begin{array}{l}\text{එබැවින් S වෘත්තයේ සමීකරණය}\left(\frac{x-3}2\right)^2+\left(\frac{y-7}2\right)^2=\frac12\\\text{එනම් }x^2+y^2-3x-7y+14=0\;\text{වේ. ➄}\end{array}————————————————————————————————————————
\begin{array}{l}(-1,2)\text{ කේන්ද්රය සහිත වෘත්තයේ සමීකරණය }x^2+y^2+2x-4y+k=0\;\text{යැයි ගනිමු.}\;\;\;➄\\\text{මෙම වෘත්තය හා S වෘත්තය ප්රලම්භව ජේදනය වන බැවින්},\\2\left(\frac{-3}2\right)(1)+2\left(\frac{-7}2\right)(-2)=k+14\;\;\Rightarrow k=-3\text{යැයි ලැබේ}.\\\text{එබැවින් වෘත්තයේ සමීකරණය }x^2+y^2+2x-4y-3=0\;\text{වේ. ➄}\end{array}- අභ්යාස :-
ප්රථම මූලධර්ම භාවිතයෙන්, වෘත්තයෙහි කේන්ද්රය හා අරය සොයන්න. x අක්ෂය මත පිහිටි ලක්ෂ්යයක සිට එම වෘත්තයට, එකිනෙකට ලම්භ ස්පර්ෂක දෙකක් අඳිනු ලැබේ. එවැනි ලක්ෂ්යය දෙකක් පවතින බව පෙන්වන්න.
\begin{array}{rcl}x^2+y^2-10x-8y+31&=&0\\(x-5)^2+(y-4)^2+31-25-16&=&0\;\;\;➄\\(x-5)^2+(y-4)^2-10&=&0\\(x-5)^2+(y-4)^2&=&10\end{array} \begin{array}{rcl}\therefore\;\text{කේන්ද්රය}&=&(5,4)\;\;\;\;\;\;\;➄\\\;\text{අරය}&=&\sqrt{10}\;\text{ඒකක}\;\;\;\;\;\;\;➄\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\boxed{15}\end{array}x අක්ෂය මත පිහිටි ලක්ෂ්යෙය් සිට වෘත්තයට ඇඳි ස්පර්ෂකයේ අනුක්රමණය m යැයි ගනිමු.
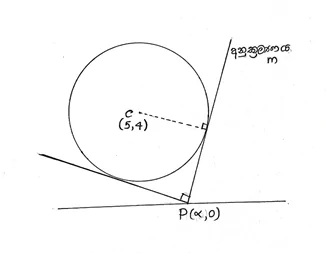
රූපයට ⑤
එවිට ස්පර්ෂකයේ සමීකරණය,
\begin{array}{rcl}y-0&=&m\left(x-\alpha\right)\\mx-y-m\alpha&=&0\;\;\;\;\;\;\;➉\end{array}වෘත්තය ස්පර්ෂ වීම සඳහා
\begin{array}{rcl}\left|\frac{\left(5-\alpha\right)m-4}{\sqrt{m^2+1}}\right|&=&\sqrt{10}\;\;\;\;\;\;⑩\\\left|\frac{5m-4-m\alpha}{\sqrt{m^2+1}}\right|&=&\sqrt{10}\\\left[(5-\alpha)m-4\right]^2&=&10(m^2+1)\\(25-10\alpha+\alpha^2-10)m^2-8(5-\alpha)m+16-10&=&0\\(\alpha^2-10\alpha+15)m^2-8(5-\alpha)m+6&=&0\;\;\;\;\;\;\;\;\;\;⑩\end{array}මෙය m හි වර්ගජ සමීකරණයකි. මූල නම්,
ස්පර්ෂක දෙක ලම්භ වීම සඳහා බැවින්, ⑤
\begin{array}{rcl}\frac6{\alpha^2-10\alpha+15}&=&-1\;\;\;\;⑤\\\alpha^2-10\alpha+21&=&0\end{array}මෙය \alpha හි වර්ගජ සමීකරණයකි. මෙහි විවේචකය, ⑤
\begin{array}{rcl}\triangle_\alpha&=&10^2-4\left(1\right)\left(21\right)\\&=&100-84\\&=&16>0\end{array}\begin{array}{rcl}\triangle_\alpha&>&0\end{array} බැවින් \alpha සඳහා තාත්වික ප්රභින්න අගයන් දෙකක් ඇත.
\begin{array}{rcl}&&\therefore\;P\left(\alpha,0\right)\end{array} ආකාරයේ ලක්ෂ්යය දෙකක් පවතී. ⑩ {\begin{array}{rcl}&&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\boxed{60}\end{array}}

