වෘත්ත ජ්යායක මධ්ය ලක්ෂයේ ඛණ්ඩාංක දී ඇති විට එම ජ්යායේ සමීකරණය සෙවීම
x2 + y2 + 2gx + 2fy + c = 0 වෘත්තයේ මධ්ය ලක්ෂ්යයේ (h,k) වන ජ්යායයේ සමීකරණය සොයමු.
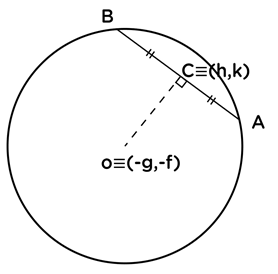
දී ඇති වෘත්තයේ කේන්ද්රය , O ≡ (-g, -f ) වේ.
\begin{array}{rcl}(oc\;\text{අනුක්රමණය})\;.\;(AB\;\text{ජ්යායයේ අනුක්රමණය})&=&-1\\(AB\;\text{ජ්යායයේ අනුක්රමණය})&=&\frac{-1}{\text{( oc අනුක්රමණය )}}\\AB\;\text{ජ්යායයේ අනුක්රමණය}&=&\frac{-1}{\left({\displaystyle\frac{(k+f)}{(h+g)}}\right)}\end{array}∴ මධ්ය ලක්ෂ්යය (h,k) වන AB ජ්යායයේ සමීකරණය,
y-k=-\left(\frac{h+g}{k+f}\right)\;\left(x-h\right)උදා : x2 + y2 = 9 වෘත්තයේ (1 , -2 ) මධ්ය ලක්ෂ්යය වශයෙන් පවත්නා ජ්යායයේ සමීකරණය සොයන්න.
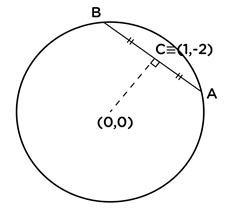
දී ඇති වෘත්තයේ කේන්ද්රය ≡ ( 0 , 0 )
\begin{array}{rcl}(oc\;\text{අනුක්රමණය})\;.\;(AB\;\text{ජ්යායයේ අනුක්රමණය})&=&-1\\AB\;\text{ජ්යායයේ අනුක්රමණය}&=&\frac{-1}{\left({\displaystyle\frac{(0+2)}{(0-1)}}\right)}\\AB\;\text{ජ්යායයේ අනුක්රමණය}&=&\frac12\end{array}∴ අවශ්ය ජ්යායයේ සමීකරණය,
\begin{array}{rcl}y+2&=&\frac12\left(x-1\right)\\2y+4&=&x–1\\x–2y–5&=&0\;\text{වේ.}\end{array}වෘත්තය මත ලක්ෂයකදී වෘත්තයට අඳින ස්පර්ෂකයේ සහ අභිලම්භයේ සමීකරණය
I ක්රමය
S≡x2 +y2+2gx+2fy+c=0 වෘත්තය මත P(x0,y0) ලක්ෂ්යයේ දී වෘත්තයට ඇඳි ස්පර්ශකයේ හා අභිලම්බයේ සමීකරණ සොයමු.
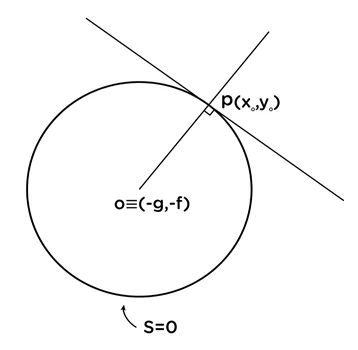
S = 0 වෘත්තයේ කේන්ද්රය , O ≡ (-g,-f )
\begin{array}{rcl}\text{අභිලම්බයේ අනුක්රමණය}&=&\left[\frac{y_0-\left(-f\right)}{x_0-\left(-g\right)}\right]\\&=&\left[\frac{y_0+f}{x_0+g}\right]\end{array}(x0,y0) ලක්ෂ්යයේ දී වෘත්තයට ඇඳි අභිලම්බයේ සමීකරණය,
y-y_0=\left[\frac{y_0+f}{x_0+g}\right]\left(x-x_0\right)\;\;\text{වේ.} \begin{array}{rcl}\text{(ස්පර්ශකයේ අනුක්රමණය).(අභිලම්බයේ අනුක්රමණය)}&=&-1\\\text{ස්පර්ශකයේ අනුක්රමණය}&=&\left[-\frac{x_0+g}{y_0+f}\right]\end{array}∴ (x0,y0) ලක්ෂ්යයේ දී වෘත්තයට ඇඳි ස්පර්ශකයේ සමීකරණය,
y-y_0=-\left[\frac{x_0+g}{y_0+f}\right]\left(x-x_0\right)\;\;\text{වේ.} \begin{array}{rcl}y–y_0&=&-\left[\frac{x_o+g}{y_0+f}\right].(x–x_0)\\yy_0+fy–y_0^2–fy_0&=&-xx_0+x_0^2–gx+gx_0\\xx_0+yy_0+gx+fy&=&x_0^2+y_0^2+gx_0+fy_0\end{array}gx0 + fy0 + c දෙපසටම එකතු කිරීමෙන් ;
\begin{array}{rcl}xx_0+yy_0+gx+fy+gx_0+fy_0+c&=&x_0^2+y_0^2+2gx_0+2fy_0+c\\xx_0+yy_0+g(x+x_0)+f(y+y_0)+c&=&0\end{array}∵ (x0,y0) ලක්ෂ්යය S = 0 වෘත්තය මත වන නිසා , එම ලක්ෂ්යයේ ඛණ්ඩාංක මඟින් වෘත්ත සමීකරණය තෘප්ත වේ.
මෙවිට x02 + y02 +2 gx0 +2 fy0 + c = 0 වේ.
ස්පර්ශකයේ සමීකරණය ලියන ආකාරය
වෘත්තයේ සමීකරණය ,
x2 + y2 + 2gx +2fy + c = 0
ස්පර්ශකයේ සමීකරණය ලිවීම සඳහා වෘත්ත සමීකරණය සැකසීම.
xx + yy + g(x+x) + f(y+y) + c = 0
(x0,y0) ලක්ෂ්යයේ දී ස්පර්ශකයේ සමිකරණය,
xx0 + yyo + g(x+x0) + f(y+y0) + c = 0
II ක්රමය
S ≡ x2 + y2 + 2gx + 2fy + c = 0 වෘත්තය මත P(x0,y0) ලක්ෂ්යය සලකමු.
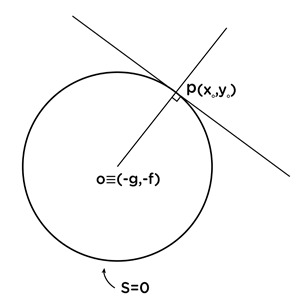
ඕනෑම (x,y) ලක්ෂ්යයක දී වක්රයකට ඇඳි ස්පර්ශකයේ අනුක්රමණය \frac{dy}{dx} වේ.
x2 + y2 + 2gx + 2fy + c = 0
x විෂයෙන් අවකලනයෙන් ,
\begin{array}{rcl}2x+2y.\frac{\operatorname dy}{\operatorname dx}+2g+2f.\frac{\operatorname dy}{\operatorname dx}+0&=&0\\\frac{\operatorname dy}{\operatorname dx}\left(2y+2f\right)&=&-(2x+2g)\\\frac{\operatorname dy}{\operatorname dx}&=&-\frac{\left(x+g\right)}{\left(y+f\right)}\\{\left[\frac{\operatorname dy}{\operatorname dx}\right]}_{\left(x_0,y_0\right)}&=&-\frac{\left(x_0+g\right)}{\left(y_0+f\right)}\&&\end{array}∴ (x0,y0) ලක්ෂ්යයේ දී වෘත්තයට ඇඳි ස්පර්ශකයේ සමිකරණය,
y-y_0=-\left[\frac{x_0+g}{y_0+f}\right].\left(x-x_0\right)(ස්පර්ශකයේ අනුක්රමණය).(අභිලම්බයේ අනුක්රමණය) = -1
⟹ අභිලම්බයේ අනුක්රමණය = \frac{y_0+f}{x_0+g}
∴ (x0,y0) ලක්ෂ්යයේ දී වෘත්තයට ඇඳි අභිලම්බයේ සමිකරණය,
y-y_0=\left[\frac{y_0+f}{x_0+g}\right].\left(x-x_0\right)උදා; x2 + y2 – 4x + 10y – 8 = 0 වෘත්තයට (3,1) ලක්ෂ්යයේ දී ඇඳි ස්පර්ශකයේ හා අභිලම්භයේ සමීකරණ සොයන්න.
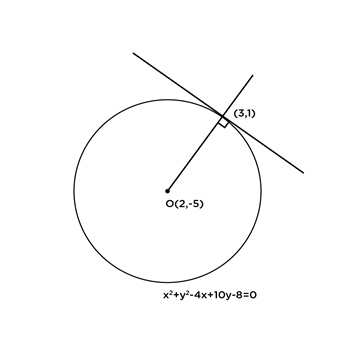
වෘත්තයේ කේන්ද්රය, O ≡ (2,-5)
\begin{array}{rcl}\text{අභිලම්භයේ අනුක්රමණය }&=&\frac{(1+5)}{(3-2)}\\&=&6\end{array}∴ (3,1) ලක්ෂ්යයේ දී වෘත්තයට ඇඳි අභිලම්බයේ සමිකරණය,
\begin{array}{rcl}y–1&=&6(x–3)\\6x–y–17&=&0\;\text{වේ.}\end{array} \begin{array}{rcl}\text{(ස්පර්ශකයේ අනුක්රමණය).(අභිලම්භයේ අනුක්රමණය)}\;&=&-1\\\text{ස්පර්ශකයේ අනුක්රමණය}\;&=&-\frac16\end{array}∴ (3,1) ලක්ෂ්යයේ දී වෘත්තයට ඇඳි ස්පර්ශකයේ සමීකරණය ,
\begin{array}{rcl}y–1&=&-\frac16(x–3)\\x+6y–9&=&0\;\text{වේ.}\end{array}වෘත්තයක් හා සරල රේඛාවක් ජේදනය වීමට,ජේදනය නොවීමට හා ස්පර්ශ වීමට අවශ්යතාවය
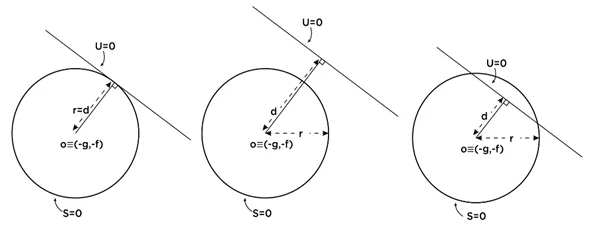
වෘත්ත කේන්ද්රයේ සිට u=0 සරල රේඛාවට ඇති ලම්භක දුර d යැයි ගනිමු .
d=\frac{\left|-lg-mf+n\right|}{\sqrt{l^2+m^2}}
U=0 සරල රේඛාව, S=0 වෘත්තය ස්පර්ශ කරයි.⇒ d=r
\begin{array}{l}\frac{\left|-lg-mf+n\right|}{\sqrt{l^2+m^2}}=\sqrt{g^2+f^2-c}\\\left(-lg-mf+n\right)^2=\left(g^2+f^2-c\right)\left(l^2+m^2\right)\end{array}
S=0 වෘත්තය ජේදනය නොකෙරේ. ⇒d>r
⇔ (lg+mf-n)2 > (g2+f2-c)(l2+m2)
S=0 වෘත්තය ජේදනය කෙරේ. ⇒ d<r
⇔ (lg+mf-n)2 < (g2+f2-c)(l2+m2)
උදා :(1.) 7x –y –1=0 රේඛාව මගින් s= x2 +y2 – 4y– 3/4=0 වෘත්තය ජේදනය වන බව පෙන්වන්න.
\begin{array}{rcl}\text{S≡}x^2+y^2-4y–\frac34&=&0\\\text{S=}x^2+y^2+2(-2)y-3⁄4&=&0\end{array} \begin{array}{rcl}\text{වෘත්තයේ කේන්ද්රය}O&\equiv&(0,2)\\r&=&\sqrt{g^2+f^2-c}\\&=&\sqrt{0+(-2)^2+3⁄4}\\r&=&\sqrt{\frac{19}2}\end{array}
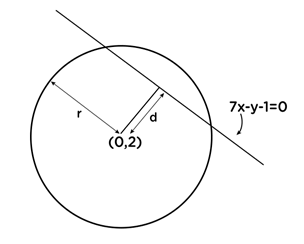
(0,2) ලක්ෂ්යයේ සිට l=0 සරල රේඛාවට ඇති ලම්භ දුර සොයමු.
\begin{array}{rcl}d&=&\frac{\left|7(0)-2-1\right|}{\sqrt{7^2+(-1)^2}}\\&=&\frac{3\sqrt2}{10}\\\frac{3\sqrt2}{10}&<&\sqrt{\frac{19}2}\\d&<&r\end{array}∴ l=0 සරල රේඛාව මගින් S=0 වෘත්තය ජේදනය කරයි.
උදා:(2.) y=2x+c සරල රේඛාව x2+y2+ 4x-10y -7=0 වෘත්තය ස්පර්ශ කරන්නේ නම් c හි අගය සොයන්න.
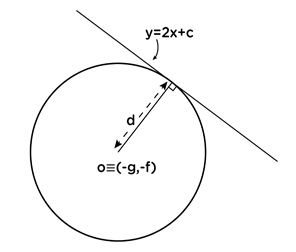
y= 2x+ c ⇒ 2x-y+c=0
මෙම සරල රේඛාවට වෘත්ත කේන්ද්රයේ සිට ඇති ලම්භක දුර d ලෙස ගනිමු.
වෘත්තය සරල රේඛාව ස්පර්ශ කරය නම් ,
\begin{array}{rcl}d&=&\frac{\left|2(-2)-5+c\right|}{\sqrt{2^2+(-1)^2}}\\&=&\frac{\left|c-9\right|}{\sqrt5}\end{array} \begin{array}{rcl}\text{r=d}\;&\Rightarrow&\;6=\frac{\left|c-9\right|}{\sqrt5}\\\pm6\sqrt5&=&c-9\\\text{c=}9+6\sqrt5\text{ හෝ }c&=&9-6\sqrt5\;\text{වේ.}\end{array}


නියමයි මේක… ගොඩාක් ප්රයෝජනවත්