ආදේශ මගින් අනුකලනය
- ආදේශය:\ t=tan({\frac{x}{2})} යොදා අනුකලනය කරමු.
උදා:
\int\frac{dx}{2+cosx}\ සලකමු.
t=\tan{\left(\frac{x}{2}\right)} ආදේශ කරමු
x විෂයෙන් අවකලනයෙන්,
\begin{array}{rcl}dt&=&\frac12\sec^2\frac x2\;dx\\dt&=&\frac12\left(1+\tan^{2\;}\frac x2\right)dx\\dt&=&\frac12\left(1+t^2\right)dx\\dx&=&\frac{2dt}{(1+t^2)}\end{array}
\begin{array}{rcl}\cos x&=&\cos^{2\;}\frac x2\;-\sin^2\frac x2\\&=&\frac{\cos^{2\;}\frac x2\;-\sin^2\frac x2}{\cos^2\frac x2+\sin^2\frac x2}\end{array}
හරය හා ලවය \begin{array}{rcl}&&\cos^{2\;}\frac x2\end{array} න් බෙදූ විට,
\begin{array}{rcl}\cos x&=&\;\frac{1-\tan^2{\displaystyle\frac x2}}{1+\;\tan^2\frac x2}\\\cos x&=&\;\frac{1-t^2}{1+t^2}\end{array}
\begin{array}{rcl}\int\frac{dx}{2+cosx}&=&\int\frac{\frac{2dt}{(1+t^2)}}{2+\left(\frac{1-t^2}{1+t^2}\right)}\\&=&\int\frac{2dt}{2+2t^2+1-t^2}\\&=&2\int\frac{dt}{t^2+3}\\&=&2\int\frac{dt}{t^2+\left(\sqrt3\right)^2}\\&=&\frac2{\sqrt3}\tan^{-1}\left(\frac t{\sqrt3}\right)\\&=&\frac2{\sqrt3}\tan^{-1}\left(\frac{\tan\frac x2}{\sqrt3}\right)+c\text{ : c යනු අභිමත නියතයකි.}\end{array}
3.\int\frac{\mathbf{dx}}{\mathbf{a}+\mathbf{bcosx}+\mathbf{csinx}\ } ආකාරයේ අනුකල
- ආදේශය: t=\tan{\left(\frac{x}{2}\right)} යොදා අනුකලනය කරමු.
උදා:
\int\frac{dx}{5+4sinx+3cosx} සලකමු.
t=\tan{\left(\frac{x}{2}\right)} ආදේශ කරමු.
x විෂයෙන් අවකලනයෙන්,
4.\int\frac{\mathbf{dx}}{\mathbf a+\mathbf b\mathbf{cos}^{\mathbf2}\mathbf x\;+\mathbf c\mathbf{sin}^{\mathbf2}\mathbf x\;} ආකාරයේ අනුකල
- ආදේශය:t=\tan x යොදා අනුකලනය කරමු.
උදා:
\int\frac{dx}{3\cos^2x-4\sin^2x-5} සලකමු.
t=\tan x ආදේශ කරමු.
x විෂයෙන් අවකලනයෙන්
\begin{array}{rcl}dt&=&\sec^2xdx\\dt&=&\left(1+\tan^{2\;}x\right)dx\\dt&=&\left(1+t^2\right)dx\\dx&=&\frac{dt}{(1+t^2)}\end{array}
\begin{array}{rcl}\sin^2x&=&\frac1{\mathrm c\mathrm o\mathrm s\mathrm e\mathrm c^2x}\\\sin^2x&=&\frac1{1+\cot^2x}\\\sin^2x&=&\frac{\tan^2x}{1+\tan^2x}\\\sin^2x&=&\frac{t^2}{1+t^2}\end{array}
\begin{array}{rcl}\cos^2x&=&\frac1{\sec^2x}\\\cos^2x&=&\frac1{1+\tan^2x}\\\cos^2x&=&\frac1{1+t^2}\end{array}
\begin{array}{rcl}\int\frac{dx}{3\cos^2\;x-4\sin^2x-5}&=&\int\frac{\frac{dt}{(1+t^2)}}{3\left(\frac1{1+t^2}\right)-4\left(\frac{t^2}{1+t^2}\right)-5}\\&=&\int\frac{2dt}{3-4t^2-5-5t^2}\\&=&\int\frac{dt}{-9t^2-2}\\&=&-\int\frac{dt}{9t^2+2}\\&=&-\frac19\int\frac{dt}{t^2+\frac29}\\&=&-\frac19\int\frac{dt}{t^2+\left(\frac{\sqrt2}3\right)^2}\\&=&-\frac19.\frac3{\sqrt2}\tan^{-1}\left(\frac t{\displaystyle\frac{\sqrt2}3}\right)+c\\&=&-\frac1{3\sqrt2}\tan^{-1}\left(\frac3{\sqrt2}\tan x\right)+c\text{ : c යනු අභිමත නියතයකි.}\end{array}
x\geq1 සඳහා y=\frac1x වක්රය x අක්ෂය වටා භ්රමණය කිරීමෙන් සෑදෙන ඝණ වස්තුව සලකන්න.
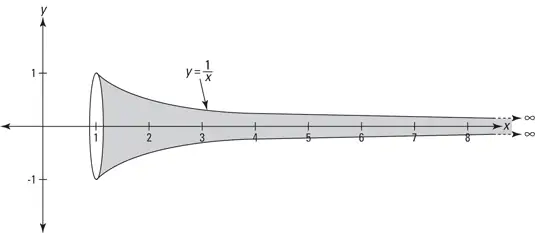
1.එම ඝණ වස්තුවේ පරිමාව සොයන්න.( y=f(x) වන ඝෘණ නොවන වක්රයක් x අක්ෂය වටා භ්රමණය කිරීමෙන් සෑදෙන ඝණ වස්තුවේ පරිමාව මෙම සමීකරණයෙන් ලබා දේ. v=\mathrm\pi\int_{\mathrm a}^{\mathrm b}{\mathrm f{(\mathrm x)}^2}\;\mathrm{dx}\;;\;\mathrm a\leq\mathrm x\leq\mathrm b )
2.y=f(x) වන ඝෘණ නොවන වක්රයක් x අක්ෂය වටා භ්රමණය කිරීමෙන් සෑදෙන ඝණ වස්තුවක මතුපිට වර්ගඵලය පහත සමීකරණයෙන් ලබා දේ.
A=2\mathrm\pi\int_{\mathrm a}^{\mathrm b}\mathrm f(\mathrm x)\;\sqrt{1+{{\mathrm f^/(\mathrm x)}}^2}\;\mathrm{dx}\;;\;\mathrm a\leq\mathrm x\leq\mathrm b
ඉහත දැක්වෙන් ඝණ වස්තුවට අසීමිත වර්ගඵලයක් හා සීමිත පරිමාවක් ඇති බව පෙන්වන්න.
5. \int\frac{\mathbf{dx}}{\left(\mathbf{px}+\mathbf{q}\right)\sqrt{\mathbf{ax}+\mathbf{b}}\; } ආකාරයේ අනුකල
- ආදේශය:\;t=\sqrt{ax+b} යොදා අනුකලනය කරමු.
උදා:
\int\frac{dx}{(x+2)\sqrt{x+1}}සලකමු.
\;t=\sqrt{x+1} ආදේශ කරමු.
x විෂයෙන් අවකලනයෙන්,
6.\int\frac{\mathbf{dx}}{\left(\mathbf{px}+\mathbf q\right)\sqrt{\mathbf{ax}^{\mathbf2}+\mathbf{bx}+\mathbf c}\;\;} ආකාරයේ අනුකල
- ආදේශය:\left(px+q\right)=\frac1t යොදා අනුකලනය කරමු.
උදා:
\int\frac{dx}{\left(x+2\right)\sqrt{x^2+x-1}}සලකමු.x+1=\frac1t ආදේශ කරමු.
x=\frac1t-1
t විෂයෙන් අවකලනයෙන්,
\begin{array}{l}\frac{dx}{dt}=-\frac1{t^2}\\dx=-\frac1{t^2}dt\end{array}
\begin{array}{rcl}\int\frac{dx}{\left(x+2\right)\sqrt{x^2+x-1}}&=&\int\frac{-\frac1{t^{2\;}}dt}{\frac1t\sqrt{\left(\frac1t-1\right)^2+\left(\frac1t-1\right)-1}}\\&=&\int\frac{dt}{\frac1t\sqrt{\frac1{t^{2\;}}-\frac2t+1+\frac1t-2}}\\&=&-\int\frac{dt}{t\sqrt{\frac{1-2t-t^2+t}{t^2}}}\\&=&-\int\frac{dt}{t.\frac1t\sqrt{1-t-t^2}}\\&=&-\int\frac{dt}{\sqrt{(-)(t^2+t-1)}}\\&=&-\int\frac{dt}{\sqrt{(-)\left[\left(t+\frac12\right)^2-1-\frac14\right]}}\\&=&-\int\frac{dt}{\sqrt{\left(\frac{\sqrt5}2\right)^2-\left(t+\frac12\right)^2}}\\&=&-\sin^{-1}\left(\frac{t+\frac12}{\displaystyle\frac{\sqrt5}2}\right)+c\\&=&-\sin^{-1}\left(\frac{\frac1{\left(x+1\right)}+\frac12}{\frac{\sqrt5}2}\right)+c\\&=&-\sin^{-1}\left(\frac{2+x+1}{\sqrt5(x+1)}\right)+c\\&=&-\sin^{-1}\left(\frac{x+3}{\sqrt5(x+1)}\right)+c\text{ : c යනු අභිමත නියතයකි.}\end{array}
7.\int{\mathbf{a}^\mathbf{x}\mathbf{dx}} ආකාරයේ අනුකල
මෙහි a යනු නියතයකි. මෙවැනි අනුකලන සදහා t=a^x හෝ k නියතයක් විට a=e^k ආදේශ කරනු ලැබේ.
a)t=a^xආදේශයෙන් ඉහත අනුකලනය සොයමු.
\begin{array}{rcl}t&=&a^x\\\ln t&=&ln\;a^x\\\ln t&=&x\;ln\;a\end{array}
x විෂයෙන් අවකලනයෙන්,
\begin{array}{rcl}\frac1t.\frac{dt}{dx}&=&\;ln\;a\\\frac1{t\ln a}.dt&=&dx\end{array}
\begin{array}{rcl}\int a^xdx\;&=&\int t.\frac1{t.lna}dt\\&=&\int\frac1{\ln a}dt\\&=&\frac1{\ln a}\int dt\\&=&\frac1{\ln a}.t+c\\&=&\frac1{\ln a}.a^x+c\text{ : c යනු අභිමත නියතයකි.}\end{array}
b) a=e^k ආදේශයෙන්\;\int a^xdx\;සොයමු.
\begin{array}{rcl}a&=&e^k\\k&=&\ln\;a\end{array}
\begin{array}{rcl}\int a^xdx\;&=&\int e^{kx}dx\;\\&=&\frac1k\;e^{kx}+c\\&=&\frac1{\ln a}.a^x+c\text{ : c යනු අභිමත නියතයකි.}\end{array}
8.\;\int\sqrt{\mathbf a^{\mathbf2}-\mathbf x^{\mathbf2}\;}\mathbf{dx}ආකාරයේ අනුකල
- මෙවැනි අනුකලන x=a\sin\theta හෝ x=a\cos\theta ආදේශ භාවිතා කරමු.
උදා.
\int\sqrt{4-x^2}dxසලකමු.
x=2\sin\theta ආදේශ කරමු.
x විෂයෙන් අවකලනයෙන්,
“Science is the Differential Calculus of the mind. Art the Integral Calculus; they may be beautiful when apart, but are greatest only when combined.”
-Ronald Ross –

