02.11.00 – ද්විපද ප්‍රසාරණය

 

 (a + b ) ⁿ  ආකාරයේ ප්‍රසාරණ සදහා ද්විපද ප්‍රමේයය භාවිතා කරයි.මෙහි a , b ∈ ℝ , n ∈ ℤ⁺ .

ක්‍රමාරෝපිත අංකනය

ධන නිඛිල සදහා පමණක් අර්ථ දැක්වේ.

5\;!=\;5\times4\times3\times2\times1\\n\;!\;=n\;\times\;(n-1)\;\times\;(n-2)\;\times\;\dots\dots\;\times\;2\;\times\;1

ⁿC_r අංකනය

0\;\leq\;r\;\leq\;n වන \;n,r\in Z⁺ විට,

                       ⁿC_r =\frac{n!}{(n-r)!r!}

 

 උදා;

\begin{array}{rcl}{}^5C_3&=&\frac{5!}{(5-3)!3!\;\;}\;\;\;\;\;\;\;\;\;\;\\&=&\frac{5!}{(2!\;3!)}\;\;\;\;\;\;\;\;\;\;\;\;\;\\&=&\frac{(5\times4\times3!)}{(2!\;3!)}\;\;\;\;\;\;\;\;\;\;\;\;\\\;&=&\frac{20}2\;\;\;\;\;\;\;\;\;\;\;\;\\\;&=&10\;\\\;{}^nC_0\;&=&\;\frac{\;\;n!\;}{0!(n-0)!}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\&=&\;1\;\;\\{}^nC_1\;&=&\;\;\frac{\;\;n!\;\;\;}{(n-1)!1!}\;\;\;\;\;\;\;\;\;\;\;\;\\&=&\;n\;\;\\{}^nC_n\;&=&\;\;\frac{\;\;n!\;}{\left[(n-n)!\;n!\right]}\;\;\;\;\;\;\;\;\;\;\\\;\;&=&\;1\end{array}

 

විශේෂ සාධන

\begin{array}{rclc}\;\;\;1)\;\;{}^nC_r\;&=&{}^nC_{(n-r)}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\\\;LHS&=&{}^nC_r=\;\frac{n!}{(n-r)!r!}&\\\;RHS&=&{}^nC_{(n-r)}&\\&=&\frac{n!}{\lbrack n-(n-r)\rbrack!(n-1)!}&\\&=&\frac{n!}{r!(n-r)!}\;\;&\\\;LHS&=&RHS\;\;\;\;&\\\;\;2){}^nC_r\;+{}^nC_{(r-1)}\;&=&{}^{(n+1)}C_r\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\\\;LHS&=&{}^nC_r+{}^nC_{(r-1)}\;\;&\\&=&\;\frac{\;n!\;}{(n-r)!r!\;}+\frac{\;\;n!}{\lbrack n-(r-1)\rbrack!(r-1)!\;}&\\\;&=&\frac{n!}{(n-r)!r\;(r-1)!}\;\;+\frac{n!}{(n-r+1)(n-r)!(r-1)!}\;\;&\\&=&\frac{n!}{(n-r)!(r-1)!}\lbrack\frac1r+\;\;\frac1{(n-r+1)}\rbrack\;\;&\\&=&\frac{n!}{(n-r)!(r-1)!}\times\frac{(n+1)}{\left[r(n-r+1)\right]}\;\;&\\&=&\frac{(n+1)!}{(n-r+1)!r!\;}&\\&=&{}^{(n+1)}C_r\;&\end{array}

උදා:- ⁿC_r  + ⁿC_{r + 1}  =  ⁿ⁺¹C_r+1 බව පෙන්වන්න එනයින් ²⁰⁰³C_r+ ²⁰⁰⁴C_r+²⁰⁰⁵C_r+…………+²⁰¹⁹C_r      =       ²⁰²⁰C_r+1 –²⁰⁰³C_r+1 බව පෙන්වන්න

\begin{array}{rcl}{}^nC_r+{}^nC_{(r+1)}&=&\frac{n!}{(n-r)!r!}+\frac{n!}{(n-r-1)!(r+1)!}\\&=&\frac{n!}{(n-r)(n-r-1)!r!}+\frac{n!}{(n-r-1)!(r+1)r!}\\&=&\frac{n!}{(n-r-1)!r!}\;\left[\frac1{(n-1)}+\frac1{(n+1)}\right]\\&=&\frac{n!}{(n-r-1)!r!}\frac{(n+1)}{(n-1)(r+1)}\\&=&\frac{(n+1)!}{(n-r)!(r+1)!}\\&=&{}^{(n+1)}C_{(r+1)}\\{}^nC_r&=&{}^{(n+1)}C_{(r+1)}-{}^nC_{(r+1)}\end{array}

 

n = 2003       ²⁰⁰³C_r = ²⁰⁰⁴C_r+1 – ²⁰⁰³C_r+1

n = 2004   ²⁰⁰⁴C_r =²⁰⁰⁵C_r+1  – ²⁰⁰⁴C_r+1

n = 2018        ²⁰¹⁸C_r  =  ²⁰¹⁹C_r+1 –  ²⁰¹⁸C_r+1

n = 2019        ²⁰¹⁹C_r+ =  ²⁰²⁰C_r+1  –  ²⁰¹⁹C_r+1

\begin{array}{l}\sum_{n=2003}^{2019}\end{array}\begin{array}{l}{}^n{C_{r\;}=\;\;{}^{2020}{C_{(r+1)}\;-}\;{}^{2003}C_{(r+1)}}\end{array}

ධන නිඛිලමය දර්ශක සදහා ද්විපද ප්‍රසාරණය

\begin{array}{rcl}(a+b)^n&=&{}^nC_0a^n+{}^n{C_1\;}a^{(n-1)}b+{}^nC_2a^{(n-2)}b^2+\dots\dots+{}^nC_{(r-1)}a^{\left[n-(r-1)\right]}b^{\left(r-1\right)}+{}^nC_ra^{\left(n-r\right)}b^r+\dots\dots.+{}^nC_nb^n\end{array}

            \begin{array}{rcl}{}^nC_r&=&\frac{n!}{(n-r)!r!}\end{array}

   ද්විපද ප්‍රසාරණය ∑ අංකනයෙන් ලිවිය හැක.

\begin{array}{rcl}(a+b)^n&=&{\textstyle\sum_{r=0}^n}\;{}^nC_ra^{n-r}b^r\end{array}

   ගණිත අභ්‍යුහන මූලධර්මය භාවිතයෙන් ධන නිඛිල සදහා ද්විපද ප්‍රමේයය සාධනය

\begin{array}{rcl}(a+b)^n&=&{}^nC_0a^n+{}^nC_1a^{(n-1)}b+\dots\dots+{}^nC_ra^{(n-r)}b^r+\dots..+{}^nC_nb^n\end{array}

 n=1 විට,

L.H.S. = \begin{array}{rcl}&&(a+b)^1\end{array}  = a+b

R.H.S. = \begin{array}{rcl}&&{}^1C_0a^1+{}^1C_1a^0b\end{array} = a+b

∴ n = 1 විට ප්‍රථිපලය සත්‍ය වේ.

n = p විට ප්‍රථිපලය සත්‍ය බව උපකල්පනය කරමු. P ∈ ℤ⁺

\begin{array}{rcl}(a+b)^p&=&{}^pC_0a^p+{}^pC_1a^{(p-1)}b+\dots\dots+{}^pC_ra^{(p-r)}b^r+\dots.+{}^pC_pb^p\end{array}

n = p + 1   විට,

\begin{array}{rcl}(a+b)^p&=&{}^pC_0a^p+{}^pC_1a^{(p-1)}b^1+\dots\dots+{}^pC_ra^{(p-r)}b^r+\dots..+{}^pC_pb^p\end{array}

 දෙපසම ( a + b ) වලින් ගුණ කරමු.

(a + b ) ^p+1 = ( a + b ) [ pC₀a^p + pC₁a^p-1b +………+pC_ra^p-rb^r+……pC_pb^p]

                     = ^pC₀a^p+1 + ^pC₁a^pb + …..+ ^pC_ra^p-r+1b^r +…..+^pC_pb^pa+

                                 ^PC₀a^pb + ^pC₁a^p-1b²+…+^pC_r-1a^p-r+1b^r+^pC_ra^p-rb^r+1+…..+^pC_pb^p+1

සාධාරණ පදය

    ( ^pC_r + ^pC_r-1) a^p-r+1b^r

   සාධනය කළ යුත්ත : ^pC_r-1 +^pC_r =^p+1C_r

       \begin{array}{rcl}\;\;\;\;\;\;\;{}^pC_{(r-1)}+{}^pC_r\;&=&\;\frac{p!}{(\;p-r+1)!(r-1)!\;}+\frac{\;p!}{(p-r)!r!}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\\;&=&\frac{\;p!(r+p-r+1)\;\;\;\;\;\;\;\;\;}{(p-r+1)!r!\;}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\\;&=&\frac{\;(p+1)!}{(p+1-r)!r!}\;\;\;\;\;\\&=&\;{}^{(p+1)}C_r\end{array}

    (^pC_r + ^pC_r-1 ) a^p-r+1b^r = ^p+1C_ra^p-r+1b^r

   ∴   ( a+ b) ^p+1 = ^p+1C₀a^p+1 +^p+1C₁a^pb +…..+^p+1C_ra^p+1-rb^r+……+^p+1C_p+1b^p+1

  ∴ n=p+1 ට ප්‍රථිපලය සත්‍යය වේ.

  ∴ සියලු (+) නිඛිල n සදහා ඉහත ප්‍රථිපලය ගණිත අභ්‍යුහන මූලධර්මයෙන් සත්‍ය වේ.

  ද්විපද ප්‍රසාරණයේ ලක්ෂණ

(a + b ) ⁿ = \begin{array}{rcl}&&{\textstyle\sum_{r=0}^n}\;\end{array}ⁿC_ra^n-rb^r

ප්‍රසාරණයට පද ( n+1) ක් ඇත.

මුලම හා අගම පදවල සංගුණක සමාන වේ.

ⁿC₀= ⁿC_n

ⁿC₁= ⁿC_n-1

ⁿC₂=ⁿC_n-2

ප්‍රසාරණයේ ඕනෑම පදයක a හා b හි බලයන්ගේ එකතුව n ට සමාන වේ.

ද්විපද ප්‍රසරණය විශේෂ අවස්ථා

1)  a=1 , b=x විට

( 1+x)ⁿ = \begin{array}{rcl}&&{\textstyle\sum_{r=0}^n}\;\end{array} ⁿC_rx^r  මෙය x වල ආරෝහණ බල පිළිවෙලයි.

( 1+x)n = \begin{array}{rcl}&&{\textstyle\sum_{r=0}^n}\;\end{array} ⁿC_rx^n-r මෙය x වල අවරෝහණ බල පිළිවෙලයි.

2) x→-x

 ( 1 -x )ⁿ= \begin{array}{l}\textstyle\sum_{r=0}^n\;\end{array}{}^nC_r{(-x)}^r=\begin{array}{l}\textstyle\sum_{r=0}^n\;\end{array}{(-1)}^r\;{}^nC_r{(x)}^r

පහත සම්බන්ධ සාධනය කරන්න.

1. (2x + 3y)⁵ එවිට n=5 වේ.

( 2x + 3y)⁵ = ⁵C₀ (2x)⁵ + ⁵C₁(2x)⁴(3y) + ⁵C₂(2x)³(3y)² + ⁵C₃(2x)²(3y)³ + ⁵C₄(2x)(3y)⁴ + ⁵C₅(3y)⁵

                  = (2x)⁵ + (2x)⁴(3y) + (2x)³(3y)² + (2x)²(3y)³ +(2x)(3y)⁴ + (3y)⁵

                  = 32x⁵ + 240x⁴y + 720x³y² + 1080x²y³ + 810xy⁴ + 243y⁵

\begin{array}{rcl}\left(x^2-\frac1x\right)^4&=&{}^4C_0{(x^2)}^4+{}^4C_1{(x^2)}^3\left(-\frac1x\right)+{}^4C_2{(x^2)}^2\left(-\frac1x\right)^2+{}^4C_3{(x^2)}\left(-\frac1x\right)^3+{}^4C_4\left(-\frac1x\right)^4\\&=&\frac{4!}{(4-0)!0!}{(x^2)}^4+\frac{4!}{(4-1)!1!}{(x^2)}^3\left(-\frac1x\right)+\frac{4!}{(4-2)!2!}{(x^2)}^2\left(-\frac1x\right)^2+\frac{4!}{(4-3)!3!}{(x^2)}\left(-\frac1x\right)^3+\frac{4!}{(4-4)!4!}\left(-\frac1x\right)^4\\&=&x^8-4x^5+6x^2-\frac4x+\frac1{x^4}\end{array}

        ඉහත ප්‍රසාරණ වල සංගුණක සුළු කිරීමේදී පියවර කෙටි කර ගැනීමට පහත ක්‍රියාපිළිවෙලා අනුගමනය කිරීම සුදුසු වේ.

\begin{array}{rcl}{}^5C_1&=&\textstyle\frac{\;5!}{(5-1)!1!\;5!\;}\\5!&=&\;5\times4\times3\times2\times1\;\;\;\;\;\;\\&=&\;5\times4!\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\\therefore{}^5C_1&=&\frac{(5\times4!)\;\;}{4!\;\;}\;\;\;\;\;\;\;\;\\\;&=&\;5\;\end{array}

මෙමගින් සුළු කිරීම පහසුය.

1. ( 1.01 ) ⁵ ආසන්න දශමස්ථාන 3කට අගයන්න.

( 1.01 ) ⁵ = (1+ 10-2 )⁵

   ( 1.01)⁵ = ⁵C₀ + ⁵C₁(10^-2) + ⁵C₂(10^-2)² + ⁵C₃(10^-2)³ + ⁵C₄(10^-2)⁴ +⁵C₅(10^-2)⁵          

         මෙහි ⁵C₀ ( 1⁵)10^-2)⁰ = ⁵C₀ පමණක් ලියනුයේ 1හි ඕනෑම බලයක අගය 1ම නිසාය.ආසන්න දශමස්ථාන 3කට සෙවිය යුතු නිසා පළමු පද 3 පමණක් සැලකීම ප්‍රමාණවත් වේ.

\begin{array}{rcl}\therefore(1.01)^5&=&\frac{5!}{5!0!}+\frac{5!}{4!1!}\times10^{(-2)}+\frac{5!}{3!2!}\times10^{(-4)}\\&=&1+\frac{(5\times4!)}{4!1!}\times10^{(-2)}+\frac{(5\times4\times3!)}{(3!\times2\times1)}\times10^{(-4)}\\&=&1.051\end{array}

• ( 0.98 )⁴ = ආසන්න දශමස්ථාන 3කට අගයන්න.

( 0.98 )⁴=  ( 1- 2×10^-2)⁴ = [ 1 + (-2×10^-2)]⁴

                = ⁴C₀ + ⁴C₁(-2×10^-2) + ⁴C₂(-2×10^-2)² + 43(-2×10-2)3 + ⁴C₄(-2×10^-2)⁴

    දශමස්ථාන 3කට අවශ්‍ය නිසා,

( 0.98)⁴ = ⁴C₀ + ⁴C₁(-2×10^-2) + ⁴C₂(-2×10^-2)²

                =   1 +  ( -2×10^-2) + (-2×10^-2)²

                =   1- 8×10^-2 +  ×4×10^-4

                       =   0.9224

                =  0.922

                                                                                                                                                                                                       මෙහිදී පළමුව a වලින්ද පසුව b වලින්ද මුළු ප්‍රසරණයම වෙන වෙනම ගුණාකර ඇත. රවුම් කර ඇති කොටස මගින් මෙම දීර්ඝ ප්‍රසරණයේ සාධාරණ පදය ලබා ගත හැක. මෙහිදී a හා b වල බලයන් සමාන වන පද ඇසුරින් සාධාරණ පදය ලබාගෙන ඇත.

ද්විපද ප්‍රසාරණයක සධාරණ ආකාරය

(x+y)ⁿ ප්‍රකාශනය සලකමු.

මෙහි සාධාරණ පදය (r+1) වන පදය ලෙස සැලකුවහොත්,

T_r+1= ⁿC_rx^n-ry^r

ඒ අනුව ප්‍රකාශනයේ r වන පදය T_r= ⁿC_r-1x^n-(r-1)y^(r-1) ලෙස ලිවිය හැක.

ද්විපද ප්‍රසාරණයක දී ඇති පදයක් සෙවීම.

(2x+y)¹⁰ හි පස්වන පදය,

\begin{array}{rcl}T_{r+1}&=&{}^{10}C_r{(2x)}^{10-r}y^r\\T_5&=&{}^{10}{C_5{(2x)}^6}y^4\\T_5&=&\frac{10!}{6!\;4!}{(2x)}^6y^4\\&=&13440x^6y^4\end{array}

ද්විපද ප්‍රසාරණයක දී ඇති පදයන්ට අනුරූප සංගුණක සෙවීම

\begin{array}{rcl}&&\left(x^2+\frac1x\right)^{10}\end{array} හි අඩංගු පදයේ සංගුණකය සොයන්න.

\begin{array}{rcl}T_{r+1}&=&{}^n{C_r{(x^2)}^{n-r}}\left(\frac1x\right)^r\end{array}

T_r+1= ¹⁰C_r(x²)^10-r(x^-1)^r

T_r+1= ¹⁰C_rx ^(20-3r)  —————– 1

¹x ^(20-3r)  = x¹¹

20-r = 11

r=3

එවිට ඉහත 1න්,

T_r+1= ¹⁰C_rx ^(20-3r) 

T₄= ¹⁰C₃ x ¹¹

සංගුණකය = ¹⁰C₃ = \begin{array}{rcl}&&\frac{10!}{7!\;3!}\end{array} = 120

ඉහත සිද්ධාන්තය භාවිතයෙන් පහත ආකාරයේ විවිධ ගැටළු විසඳිය හැක.

(1). \begin{array}{rcl}&&\left[2x+\frac k{2x}\right]^9\end{array} ප්‍රකාශනයේ x⁵හි සංගුණකය 128 ක් වේ. k වල අගයන් සොයන්න.

\begin{array}{rcl}T_{r+1}&=&{}^n{C_r\left(2x\right)}^{n-r}\left(\frac k{2x}\right)^r\\&=&{}^9{C_r\left(2x\right)}^{9-r}\left(\frac k{2x}\right)^r\\&&\end{array}

T_r+1= ⁹C_r (k^r) 2^(9-2r)x^(9-2r) —————– 1

x⁵=x^9-2r

r=2

එවිට ඉහත 1න්,

T₃= ⁹C₂  (k²)  (2⁵) x⁵

X⁵ හි සංගුණකය   128 = ⁹C₂  (k²)  (2⁵)

\begin{array}{rcl}128&=&\frac{9!}{7!\;2!}32k^2\\k^2&=&\frac19\\k&=&\pm\frac13\\&&\end{array}

(2). (1+x-ax²)⁵ ප්‍රකාශනය සලකමු. මෙහි a යනු තාත්වික නියතයකි. X හි ආරෝහණ බල පිලිවෙළින් ප්‍රසාරණය කල විට r=1,2,3,4,—,10 සඳහා x^r හි සංගුණකය A_r නම් (A₁– A₂)+( A₃– A₄)+—+( A₉ -A₁₀)=1+a⁵ බව සාධනය කරන්න.

(1+x-ax²)⁵ = 1+ A₁x+  A₂x²+—-+A₁₀x¹⁰ ——————- *

ඉහත * හි x=-1 ලෙස යෙදූ විට,

(-a)= 1- A₁+ A₂– A₃+—+A₁₀

එමනිසා,

(A₁– A₂)+( A₃– A₄)+—+( A₉ -A₁₀)=1+a⁵

(3). ධන නිඛිලමය දර්ශකයක් සඳහා ද්විපද ප්‍රසාරණය යොදා ගනිමින් \left(1+\sqrt3\right)^6+\left(1+\sqrt3\right)^6=416 බව පෙන්වන්න. එනයින් \left(1+\sqrt3\right)^6 හි පූර්ණ සංඛ්‍යාත්මක කොටස් සොයන්න.

\begin{array}{rcl}(1+\sqrt3)^6&=&{}^6C_0+{}^6C_1(\sqrt3)+{}^6C_2(\sqrt3)^2+{}^6C_3(\sqrt3)^3+{}^6C_4(\sqrt3)^4+{}^6C_5(\sqrt3)^5+{}^6C_6(\sqrt3)^6------------------1\\(1-\sqrt3)^6&=&{}^6C_0-{}^6C_1(\sqrt3)+{}^6C_2(\sqrt3)^2-{}^6C_3(\sqrt3)^3+{}^6C_4(\sqrt3)^4-{}^6C_5(\sqrt3)^5+{}^6C_6(\sqrt3)^6------------------2\\&&1+2,\\(1+\sqrt3)^6+(1-\sqrt3)^6&=&2{({}^6C_0+{}^6C_2(\sqrt3)^2+{}^6C_4(\sqrt3)^4+{}^6C_6(\sqrt3)^6})\\&=&2({1+(15\times3)+(15\times9)+27)}\\&=&2(1+180+27)\\&=&416\\(1+\sqrt3)^6&=&416-(1-\surd3)^6\\0&<&(1-\sqrt3)6<1\;\;\;\;\;\;\;\lbrack0<(1-\sqrt3)<1\rbrack\end{array}

එමනිසා, \left(1+\sqrt3\right)^6හි නිඛිල කොටස 415 වේ.

(4). (1+ x)ⁿ ද්විපද ප්‍රසාරණයේ අනුයාත සංගුණ්ක 3ක් ගුණෝත්තර ශ්‍රේඪියක පැවැතිය නොහැකි බව සාධනය කරන්න.

(1+ x)ⁿ අනුයාත සංගුණ්ක 3ක් ගුණෝත්තර ශ්‍රේඪියක පවතී යැයි ගනිමු.

අනුයාත සංගුණක 3 ⁿC_r-1, ⁿC_r , ⁿC_r+1 යැයි ගනිමු.

ගුණෝත්තර ශ්‍රේඪියක පිහිටන නිසා,

\frac{{}^nC_r}{{}^nC_{r-1}}=\frac{{}^nC_{r+1}}{{}^nC_r} විය යුතුය.

L.H.S.=>\frac{n!}{(n-r)!r!}\div\frac{n!}{\left[n-\left(r-1\right)\right]!\left(r-1\right)!}

            =\frac{n!}{(n-r)!r!}\div\frac{n!}{\left[n-\left(r-1\right)\right]!\left(r-1\right)!}

R.H.S.=>\frac{n!}{\left[n-\left(r+1\right)\right]!\left(r+1\right)!}\div\frac{n!}{\left(n-r\right)!r!}

            = \frac{\left(n-r\right)}{\left(r+1\right)}

L.H.S ≠  R.H.S

මෙය විසංවාදයකි.

එමනිසා අනුයාත සංගුණක තුන ගුණෝත්තර ශ්‍රේඪියක නොපිහිටයි.

(5) n€Z⁺ යැයි ගනිමු. x හි ආරෝහණ බලවලින් (1+x)ⁿ හි ද්විපද ප්‍රසාරණය ලියා දක්වන්න. ඉහත ප්‍රසාරණයේ අනුයාත පද දෙකක සංගුණක සමාන නම්, n ඔත්තේ වන බව පෙන්වන්න.

මෙම ගැටළුව සඳහා පහත පරිදි ලකුණු වෙන් කරයි.

(1+x²)ⁿ = ⁿC_r x^r , මෙහි {}^nC_r=\frac{n!}{r!\left(n-r\right)!} , r=1,2,3,…,n

ⁿC₀=1

අනුයාත පද දෙකක් ⁿC_r , ⁿC_r+1 ලෙස ගත හැක.

ⁿC_r =  ⁿC_r+1            මෙහි r€{0,2,3,…,n-1 }

<=> \frac{n!}{\left(n-r\right)!r!}=\frac{n!}{\left(n-r-1\right)!\left(r+1\right)!}

<=> \frac1{n-r}=\frac1{r+1}

<=> ( n-r) = (r+1)                                                                                                                                                 

<=> n = 2r+1

එමනිසා, n ඔත්තේ වේ.

ද්විපද ප්‍රසාරණයක සංගුණක අතර සම්බන්ධය.

උදා:- 1. (1+ x)ⁿ = C₀+ C₁x+ C₂x²+ C₃x³+–+ C_nxⁿ     ප්‍රසාරණය සළකා පහත ප්‍රතිඵල ලබා ගන්න.

1. C₀+ C₁+ C₂+ C₃+—+ C_n = 2ⁿ

(1+ x)ⁿ =   C₀+ C₁x+ C₂x²+ C₃x³+—+ C_nxⁿ    

X=1 විට,

2ⁿ= C₀+ C₁+ C₂+ C₃+—+ C_n

1. C₀+ C₂+ C₄+—– = C₁+ C₃+ C₅+ —– = 2^n-1

(1+ x)ⁿ =   C₀+ C₁x+ C₂x²+ C₃x³+—+ C_nxⁿ    

X=1 විට,

2ⁿ= C₀+ C₁+ C₂+ C₃+—+ C_n—————– A

X=-1 විට,

0= C₀– C₁+ C₂– C₃+——————-B

A+B                                               2ⁿ = 2C₀+ 2C₂+ 2C₄+—–

                                                        2ⁿ =2 {C₀+ C₂+ C₄+—–}

                                                        2^n-1= C₀+ C₂+ C₄+—–

A-B                                                -2ⁿ = -2C₁ -2C₃ -2C₅– —–

                                                        -2ⁿ = -2{ C₁+ C₃+ C₅+ —– }

                                                        2^n-1= C₁+ C₃+ C₅+ —–

එමනිසා,

C₀+ C₂+ C₄+—– = C₁+ C₃+ C₅+ —– = 2^n-1

1. C₁+ 2C₂+ 3C₃+—+ nC_n= n.2^n-1

(1+ x)ⁿ = C₀+ C₁x+ C₂x²+ C₃x³

දෙපසම x විශයෙන් වරක් අවකලනයෙන්,

\begin{array}{rcl}\frac{\operatorname d{(1+x)n}}{\operatorname dx}&=&\frac{\operatorname d{(C0+C1x+C2x2+C3x3)}}{\operatorname dx}\end{array}

                                                        n(1+x)^n-1 = C₁+ 2C₂x+ 3C₃x²+—

                                                        x=1 විට,

                                                        =C₁+ 2C₂+ 3C₃+—+ nC_n= n.2^n-1

උදා:- 2. සුදුසු ප්‍රසාරණ දෙකක ගුණිතය සලකා පහත ප්‍රතිඵල ලබාගන්න.

C₀C₁+ C₁C₂+ C₂C₃+—-+ C_n-1C_n= \frac{\left(2n\right)!}{\left(n+1\right)!\left(n-1\right)!}

සටහන:-

ද්විපද සංගුණක අතර ගුණිතය ඇතුලත් සංගුණක සම්බන්ධතා සාධනයේදී (1+ x)ⁿ හා (x+1)ⁿ ප්‍රසාරණය භාවිතා කල හැක.

(1+ x)ⁿ = C₀+ C₁x+ C₂x²+ C₃x³ +—+ C_nxⁿ

(1+ x)ⁿ×(x+1)ⁿ=(1+ x)²ⁿ

එවිට,  (x+1)ⁿ= C₀xⁿ+ C₁x^n-1+—+ C_n වේ.

(C₀+ C₁x+ C₂x²+ C₃x³ +—+ C_nxⁿ)× (C₀xⁿ+ C₁x^n-1+—+ C_n) =(1+ x)²ⁿ

දෙපසම x^n-1 හි සංගුණක සළකා,

 

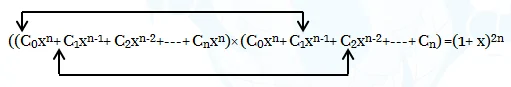
C₀C₁+ C₁C₂+ C₂C₃+—- = ²ⁿC_n-1

C₀C₁+ C₁C₂+ C₂C₃+—- = \frac{\left(2n\right)!}{\left(n+1\right)!\left(n-1\right)!}බව පෙන්වන්න

උදා:-3. C_0-\frac{C_1}2+\frac{C_2}3-\frac{C_3}{4}\;+\_\;\_\;\_\;+\frac{\left\lbrack\left(-1\right)^nC_n\right\rbrack}{n+1}=\frac1{n+1} බව පෙන්වන්න.

(1+ x)ⁿ = C₀+ C₁x+ C₂x²+ C₃x³ +—

දෙපසම x  විශයෙන් අනුකලනයෙන්,

\frac{\left(1+x\right)^{n+1}}{n+1}=C_0x+C_1\frac x2+C_2\frac{x^3}3+\_\;\_\;\_+k

K යනු නියතයකි.

x=0 විට,

\frac1{n+1}=k

x=-1 විට,

0=-C_0+\frac{C_1}2-\frac{C_2}3+\frac{C_3}{4}\;+\_\;\_\;\_\;+\frac1{n+1}

දෙපසම (-1) න් ගුණකල විට,

C_0-\frac{C_1}2+\frac{C_2}3-\frac{C_3}4+\_\;\_\;\_\;+\frac{\left[\left(-1\right)^nC_n\right]}{n+1}=\frac1{n+1}

ද්විපද සංගුණක වර්ගයන්ගේ එකතුව

(1+ x)²ⁿ=(1+ x)ⁿ. (x+1)ⁿ යැයි ගනිමු.

 

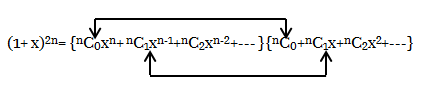
මෙහි දෙපස  වල සංගුණක සමාන කිරීමෙන්,

²ⁿC_n= (ⁿC₀)²+( ⁿC₁)²+( ⁿC₂)³+—

මෙහිදී, (1+ x)²ⁿ=  ²ⁿC_r x^r   ලෙස ලිවිය හැක.

x හි xⁿ වල සංගුණකය යනු  r=n  විටය.

එමනිසා,

වම්පස කොටසේ හි සංගුණකය වන්නේ, ²ⁿC_n

“The axiom of conditioned repetition, like the binomial theorem, is nothing but a piece of insolence.”
-Edward Abbey –