න්යාය දේශ නියමය
- එකතු කිරීම ගණිත කර්මය යටතේ සංකීර්ණ සංඛ්යා න්යාය දේශ වේ.
Z1 + Z2 = Z2 + Z1
- ගුණ කිරීමේ ගණිත කර්මය යටතේ සංකීර්ණ සංඛ්යා න්යාය දේශ වේ.
Z1 . Z2 = Z2 . Z1
සංඝට්ටන නියමය
- එකතු කිරීම යටතේ සංකීර්ණ සංඛ්යා සංඝට්ටනය වේ.
Z1 + (Z2 + Z3) = (Z1 + Z2) + Z3
සංකීර්ණ සංඛ්යාවක ප්රතිබද්ධය
- Z නම් සංකීර්ණ සංඛ්යාවේ ප්රතිබද්ධය \overline Zලෙස සංකේතවත් වේ.
Z = x + iy x,y \begin{array}{l}\in\\\end{array} R
\begin{array}{l}\overline{\mathrm Z}\;=\;\mathrm x\;-\;\mathrm{yi}\\\end{array} \begin{array}{l}\mathrm 1.Z\;=\;3\;+\;2\mathrm i\\\overline{\mathrm Z}\;=\;3\;-\;2\mathrm i\\\end{array} \begin{array}{l}\mathrm 2.Z\;=\;3\mathrm i\\\overline{\mathrm Z}\;=\;-3\mathrm i\\\end{array} \begin{array}{l}\mathrm 3.Z\;=\;4\\\mathrm Z\;=\;4\;+\;0\mathrm i\\\overline{\mathrm Z}\;=\;4\;-\;0\mathrm i\\\overline{\mathrm Z}\;=\;4\;\\\end{array} \begin{array}{l}\mathrm 4.Z\;=\;5\;-\;4\mathrm i\\\overline{\mathrm Z}\;=\;5\;+\;4\mathrm i\\\\\end{array}එක්තරා සිසුන් කණ්ඩායමක් පාසල් විද්යාගාරයේ විශේෂිත තත්ත්ව සහිත කුටීරයක බැක්ටීරියා නියැදියක වර්ධනය නිරීක්ෂණය කිරීමට ක්රියාකාරකමක් සැලසුම් කළා.
මෙය මිනිත්තු 9 ක් තුළ සිදු කළ යුතු පරීක්ෂණයක්.නමුත් ගැටලුව වුණේ ගුරුතුමිය සිසුන්ට වේලාව මැන ගැනීමට සපයා තිබුණේ මිනිත්තු 4 හා මිනිත්තු 7 වැලි ඔරලෝසු දෙකක් පමණයි
වෙනත් කිසිදු වේලාව මැන ගැනීමේ උපකරණයක් සපයා තිබුණේ නැහැ .ඔවුන්ට මෙම ඔරලෝසු දෙකෙන් පමණක් පරීක්ෂණය මිනිත්තු 9 න් කිරීමට හැකි වේවිද ?
ඊට ක්රමයක් යෝජනා කරන්න ඔබටත් පුළුවන් ද?

සංකීර්ණ සංඛ්යා හා එහි ප්රතිබද්ධ සම්බන්ධ ප්රමේයයන්
ප්රමේයය 1
Z + \displaystyle{\begin{array}{l}\overline{\mathrm Z}\\\end{array}} = 2 Re Z
සාධනය
Z = x + iy x,y \begin{array}{l}\in\\\end{array} R
\begin{array}{l}\overline{\mathrm Z}\;=\;\mathrm x\;-\;\mathrm{yi}\\\end{array} \begin{array}{rcl}Z+\overline Z&=&\left(x+iy\right)+\left(x-iy\right)\\&=&2x\\&=&2\;Re\;Z\end{array}ප්රමේයය 2
Z – \displaystyle{\begin{array}{l}\overline{\mathrm Z}\\\end{array}} = 2 Im Z
සාධනය
Z = x + iy x,y \begin{array}{l}\in\\\end{array} R
\begin{array}{l}\overline{\mathrm Z}\;=\;\mathrm x\;-\;\mathrm{yi}\\\end{array} \begin{array}{rcl}Z-\overline Z&=&\left(x+iy\right)-\left(x-iy\right)\\&=&2iy\\&=&2\;Im\;Z\end{array}ප්රමේයය 3
\begin{array}{l}\mathrm Z.\overline{\mathrm Z}\;=\;\left|Z\right|^2\end{array}සාධනය
Z = x + iy x,y \begin{array}{l}\in\\\end{array} R
\begin{array}{l}\overline{\mathrm Z}\;=\;\mathrm x\;-\;\mathrm{yi}\\\end{array} \begin{array}{rcl}\mathrm Z\;.\;\overline{\mathrm Z}\;&=&\;(\mathrm x\;+\;\mathrm{yi})(\mathrm x\;-\;\mathrm{yi})\\&=&\;\mathrm x^2\;+\;\mathrm y^2\\&=&\;\sqrt{\mathrm x^2\;+\;\mathrm y^2}\\&=&\;\left|\mathrm Z\right|^2\\&&\\&&\end{array}ප්රමේයය 4
|Z| = \begin{array}{rcl}&&\left|\overline{\mathrm Z}\right|\end{array}
සාධනය
Z = x + iy x,y \begin{array}{l}\in\\\end{array} R
\begin{array}{l}\left|\mathrm Z\right|\;=\;\sqrt{\mathrm x^{2\;}+\;\mathrm y^2}\;\;\;\leftarrow\boxed1\\\\\\\end{array} \begin{array}{rcl}\left|\mathrm Z\right|\;&=&\;\sqrt{\mathrm x^{2\;}+\;\mathrm y^2\;}\;\;\leftarrow\boxed1\\\overline{\mathrm Z}\;&=&\;\mathrm x\;-\;\mathrm{yi}\;\\\left|\overline{\mathrm Z}\right|\;&=&\;\sqrt{\mathrm x^{2\;}+\;(-\mathrm y)^2\;}\\&=&\;\sqrt{\mathrm x^{2\;}+\;\mathrm y^2\;}\;\;\leftarrow\boxed2\\\boxed1\;&=&\;\boxed2\\\left|\mathrm Z\right|\;&=&\;\left|\overline{\mathrm Z}\right|\\&&\end{array}ප්රමේයය 5
\overline{\overline Z}= Z
සාධනය
Z = x + iy x,y \begin{array}{l}\in\\\end{array} R
\displaystyle{\begin{array}{l}\overline{\mathrm Z}\\\end{array}} = x – iy
\overline{\overline Z}= x + iy
\overline{\overline Z} = Z
ප්රමේයය 6
\begin{array}{l}\overline{{\mathrm Z}_1\;+\;{\mathrm Z}_2}\;=\;\overline{{\mathrm Z}_1}\;+\;\overline{{\mathrm Z}_2}\\\end{array}- එකතුවේ ප්රතිබද්ධය ප්රතිබද්ධවල එකතුවට සමාන වේ.
සාධනය
Z1 = x1 + iy1 x1,y1 \begin{array}{l}\in\\\end{array} R
Z2 = x2 + iy2 x2,y2 \begin{array}{l}\in\\\end{array} R
\begin{array}{rcl}Z_1+Z_2&=&\left(x_1+iy_1\right)+\left(x_2+iy_2\right)\\&=&\left(x_1+x_2\right)+\left(y_1+y_2\right)i\\\overline{Z_1+Z_2}&=&\left(x_1+x_2\right)-\left(y_1+y_2\right)i\\&=&\left(x_1-y_1i\right)+\left(x_2-y_2i\right)\\\overline{Z_1+Z_2}&=&\overline{Z_1}+\overline{Z_2}\end{array}ප්රමේයය 7
\begin{array}{l}\overline{{\mathrm Z}_1\;-\;{\mathrm Z}_2}\;=\;\overline{{\mathrm Z}_1}\;-\;\overline{{\mathrm Z}_2}\\\end{array}- අන්තරයේ ප්රතිබද්ධය ප්රතිබද්ධවල අන්තරයට සමාන වේ.
සාධනය
Z1 = x1 + iy1 x1,y1 \begin{array}{l}\in\\\end{array} R
Z2 = x2 + iy2 x2,y2 \begin{array}{l}\in\\\end{array} R
\begin{array}{rcl}Z_1-Z_2&=&\left(x_1+iy_1\right)-\left(x_2+iy_2\right)\\&=&\left(x_1-x_2\right)+\left(y_1-y_2\right)i\\\overline{Z_1-Z_2}&=&\left(x_1-x_2\right)-\left(y_1-y_2\right)i\\&=&\left(x_1-y_1i\right)-\left(x_2-y_2i\right)\\\overline{Z_1-Z_2}&=&\overline{Z_1}-\overline{Z_2}\end{array}ප්රමේයය 8
\begin{array}{l}\overline{{\mathrm Z}_1{\mathrm Z}_2}\;=\;\overline{{\mathrm Z}_1}.\overline{{\mathrm Z}_2}\;\\\end{array}- ගුණිතයේ ප්රතිබද්ධය ප්රතිබද්ධවල ගුණිතයට සමාන වේ.
Z1 = x1 + iy1 x1,y1 \begin{array}{l}\in\\\end{array} R
Z2 = x2 + iy2 x2,y2 \begin{array}{l}\in\\\end{array} R
\begin{array}{rcl}Z_1Z_2&=&\left(x_1+iy_1\right)\left(x_2+iy_2\right)\\&=&\left(x_1x_2-y_1y_2\right)+i\left(x_2y_1+x_1y_2\right)\\&&\\\overline{Z_1Z_2}&=&\left(x_1x_2-y_1y_2\right)-i\left(x_2y_1+x_1y_2\right)\leftarrow\boxed1\\&&\\\overline{Z_1}.\overline{Z_2}&=&\left(x_1-y_1i\right)\left(x_2-y_2i\right)\\&=&(x_1x_2\;–\;y_1y_2)\;+\;i(-x_1y_2\;–\;x_2y_1)\\&=&(x_1x_2\;–\;y_1y_2)\;–\;i(x_1y_2\;+\;x_2y_1)\leftarrow\boxed2\\\boxed1&=&\boxed2\\\overline{Z_1Z_2}&=&\overline{Z_1}.\overline{Z_2}\end{array}ප්රමේයය 9
\begin{array}{l}\frac{\overline{{\mathrm Z}_1}}{\overline{{\mathrm Z}_2}}\;=\;\overline{\left(\frac{{\mathrm Z}_1}{{\mathrm Z}_2}\right)}\\\end{array}- බෙදීමක ප්රතිබද්ධය ප්රතිබද්ධවල බෙදීමට සමාන වේ.
Z1 = x1 + iy1 x1,y1 \begin{array}{l}\in\\\end{array} R
Z2 = x2 + iy2 x2,y2 \begin{array}{l}\in\\\end{array} R
\begin{array}{l}\overline{\left(\frac{{\mathrm Z}_1}{{\mathrm Z}_2}\right)}\\\end{array} =\frac{\left(x_1x_{{}2}+y_1y_2\right)}{\left(x_2^2+y_2^2\right)}-\frac{\left(x_2y{{}_1}-x_1y_2\right)i}{\left(x_2^2+y_2^2\right)}\begin{array}{l}\leftarrow\boxed1\\\end{array}
\begin{array}{rcl}\frac{\overline{Z_1}}{\overline{Z_2}}&=&\frac{(x_1\;-\;iy_1)}{(x_2\;-\;iy_2)}\\&=&\frac{\lbrack(x_1\;–\;y_1i)(x_2\;+\;y_2i)\rbrack\;}{\lbrack(x_2\;–\;y_2i)(x_2\;+\;y_2i)\rbrack}\\&=&\frac{\displaystyle(x_1x_2\;+\;y_1y_2)}{\displaystyle\left(x_2^2+y_2^2\right)}-\frac{\displaystyle\;(x_2y_1\;–\;x_1y_2)i}{\displaystyle\left(x_2^2+y_2^2\right)}\leftarrow\boxed2\end{array} \begin{array}{l}\boxed1\;=\;\boxed2\\\end{array} \begin{array}{l}\frac{\overline{{\mathrm Z}_1}}{\overline{{\mathrm Z}_2}}\;=\;\overline{\left(\frac{{\mathrm Z}_1}{{\mathrm Z}_2}\right)}\\\end{array}සංකීර්ණ සංඛ්යාවක මාපාංකය
- සංකීරණ සංඛ්යාවක මාපාංකය (Z) ලෙස සංකේතවත් කරන අතර එහි අර්ථය පහත පරිදි වේ.
- සංකීර්ණ සංඛ්යාවක මාපාංකය සැමවිටම ශුන්ය හෝ ධන අගයකි.
උදා:
\begin{array}{l}1.\;\mathrm Z\;=\;3\;+4\mathrm i\;\\\;\;\;\left|\mathrm Z\right|\;=\;\sqrt{3^2\;+4^2}\;=\;5\\\\2.\;\mathrm Z\;=\;2\;-\;7\mathrm i\;\\\;\;\;\left|\mathrm Z\right|\;=\;\sqrt{2^2\;+7^2}\;=\;\sqrt{53}\\\end{array}- යම් සංකීර්ණ සංඛ්යාවක මාපාංකය එහි ප්රතිබද්ධයේ මාපාංකයට සමාන වේ.
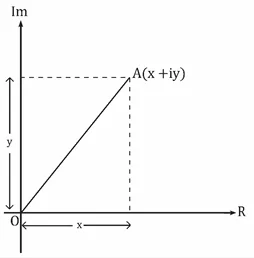
යම් සංකීර්ණ සංඛ්යාවක් ආගන්ඩ් සටහනක නිරූපණය කළ විට එහි මාපාංකය අර්ථ දැක්වෙන්නේ ඉහත පරිදිය.
- සංකීර්ණ සංඛ්යාවක ප්රතිබද්ධය හා මාපාංකය අතර සම්බන්ධය
Z = x + iy නම්, \begin{array}{l}\overline{\mathrm Z}\;=\;\mathrm x\;-\;\mathrm{iy}\\\end{array}
\begin{array}{rcl}\mathrm Z\;.\;\overline{\mathrm Z}\;&=&\;(\mathrm x\;+\;\mathrm{iy})(\mathrm x\;-\;\mathrm{iy})\\&=&\;\mathrm x^2\;-\;\mathrm{ixy}\;+\;\mathrm{ixy}\;-\;\mathrm i^2\mathrm y^2\\&=&\;\mathrm x^2\;+\;\mathrm y^2\\&=&\;(\sqrt{\mathrm x^2\;+\;\mathrm y^2})^2\\&=&\;\left|\mathrm Z\right|^2\\&&\end{array}{\mathrm Z}_1\;=\;{\mathrm x}_1\;+\;{\mathrm{iy}}_1 හා {\mathrm Z}_2\;=\;{\mathrm x}_2\;+\;{\mathrm{iy}}_2 නම්,
\begin{array}{rcl}\left|{\mathrm Z}_1.{\mathrm Z}_2\right|\;&=&\;\left|({\mathrm x}_1\;+\;{\mathrm{iy}}_1)\times({\mathrm x}_2\;+\;{\mathrm{iy}}_2)\right|\\&=&\;\left|({\mathrm x}_1{\mathrm x}_2\;-\;{\mathrm y}_1{\mathrm y}_2)+({\mathrm x}_1{\mathrm y}_2\;+\;{\mathrm y}_1{\mathrm x}_2)\right|\\&=&\;\sqrt{({\mathrm x}_1{\mathrm x}_2\;-\;{\mathrm y}_1{\mathrm y}_2)^2+({\mathrm x}_1{\mathrm y}_2\;+\;{\mathrm y}_1{\mathrm x}_2)^2}\\&=&\;\sqrt{\mathrm x_1^2(\mathrm x_2^2\;+\;\mathrm y_2^2)+\mathrm y_1^2(\mathrm x_2^2\;+\;\mathrm y_2^2)}\\&=&\;\sqrt{(\mathrm x_1^2\;+\;\mathrm y_1^2)}.\sqrt{(\mathrm x_2^2\;+\;\mathrm y_2^2)}\\\left|{\mathrm Z}_1.{\mathrm Z}_2\right|\;&=&\;\left|{\mathrm Z}_1\right|.\left|{\mathrm Z}_2\right|\end{array}- සංකීර්ණ සංඛ්යා දෙකක බෙදීමේ මාපාංකය
\begin{array}{rcl}\left|{\mathrm Z}_1\right|\;&=&\;\left|\left(\frac{{\mathrm Z}_1}{{\mathrm Z}_2}\times{\mathrm Z}_2\right)\right|\;;\;{\mathrm Z}_2\end{array} ≠ \;0යැයි ගනිමු
\begin{array}{rcl}\left|Z_1\right|&=&\left|\frac{\displaystyle Z_1}{\displaystyle Z_2}\right|\times\left|Z_2\right|\\\frac{\left|Z_1\right|}{\left|Z_2\right|}&=&\left|\frac{Z_1}{Z_2}\right|\end{array}- එනම් සංකීර්ණ සංඛ්යා දෙකක බෙදීමෙහි මාපාංකය මාපාංකවල බෙදීමට සමාන වේ.
\left|{\mathrm Z}_1+{\mathrm Z}_2\right|^2\;=\;\left|{\mathrm Z}_1\right|^2\;+\;2\mathrm{Re}({\mathrm Z}_1{\overline{\mathrm Z}}_2)\;+\;\left|{\mathrm Z}_2\right|^2 බව සාධනය කිරීම
\begin{array}{l}\left|{\mathrm Z}_1+{\mathrm Z}_2\right|^2\;=\;\left|({\mathrm x}_1+{\mathrm{iy}}_1)+({\mathrm x}_2+{\mathrm{iy}}_2)\right|^2\\=\;\left|({\mathrm x}_1+{\mathrm x}_2)+\mathrm i({\mathrm y}_1+{\mathrm y}_2)\right|^2\\=\;\left|\sqrt{({\mathrm x}_1+{\mathrm x}_2)^2+({\mathrm y}_1+{\mathrm y}_2)^2}\right|^2\\=\;\mathrm x_1^2\;+\;2{\mathrm x}_1{\mathrm x}_2\;+\;\mathrm x_2^2\;+\;\mathrm y_1^2\;+\;2{\mathrm y}_1{\mathrm y}_2\;+\;\mathrm y_2^2\\=\;\sqrt{(\mathrm x_1^2+\mathrm y_1^2)}^2\;\;+\;2({\mathrm x}_1{\mathrm x}_2\;+\;{\mathrm y}_1{\mathrm y}_2)\;+\;\sqrt{(\mathrm x_2^2+\mathrm y_2^2)}^2\\{\mathrm Z}_1{\overline{\mathrm Z}}_2\;=\;{({\mathrm x}_1+{\mathrm{iy}}_1){({\mathrm x}_2-{\mathrm{iy}}_2)}}\\=\;{({\mathrm x}_1{\mathrm x}_2\;+\;{\mathrm y}_1{\mathrm y}_2)}\;+\;\mathrm i({\mathrm y}_1{\mathrm x}_2\;-\;{\mathrm x}_1{\mathrm y}_2)\;\mathrm{නිසා}\;,\\\left|{\mathrm Z}_1+{\mathrm Z}_2\right|^2\;=\;\left|{\mathrm Z}_1\right|^2\;+\;2\mathrm{Re}({\mathrm Z}_1{\overline{\mathrm Z}}_2)\;+\;\left|{\mathrm Z}_2\right|^2\end{array}නිදසුන 01
\begin{array}{l}\frac{(-1+\mathrm i)^3}{(1+\mathrm i)^4}\end{array} සංකීර්ණ සංඛ්යාවේ මාපාංකය සොයන්න.
\begin{array}{l}Z_1\;=\;(-1+i)\end{array} නම්, \begin{array}{l}Z_2\;=\;(1+i)\end{array} නම්,
\begin{array}{l}\left|Z_1\right|\;=\;\sqrt2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left|Z_2\right|\;=\;\sqrt2\;\;\\\left|\frac{(-1+i)^3}{(1+i)^4}\right|=\left|\frac{Z_1^3}{Z_2^4}\right|=\frac{\left|Z_1\right|^3}{\left|Z_2\right|^4}=\frac{\sqrt2^3}{\sqrt2^4}=\frac1{\sqrt2}\end{array}නිදසුන 02
Z = x + iy යනු සංකීර්ණ සංඛ්යාවක් යැයි ගනිමු. මෙහි x,y \begin{array}{l}\in\\\end{array} R වේ. \begin{array}{l}\left|\mathrm Z\right|^2\;=\;\mathrm Z.\overline{\mathrm Z}\;\;\;\;\mathrm{හා}\;\;\;\mathrm Z\;-\;\overline{\mathrm Z}\;=\;2\mathrm i\;\mathrm{ImZ}\end{array} බව පෙන්වන්න. එනයින් \begin{array}{l}\left|\mathrm Z\;-\;3\mathrm i\right|^2\;=\;\left|\mathrm Z\right|^2\;-\;6\mathrm{ImZ}\;+\;9\;\mathrm{හා}\;\left|1\;+\;3\mathrm{iZ}\right|^2\;-\;9\left|\mathrm Z\right|^2\;-\;6\mathrm{ImZ}\;+\;1\end{array} බව පෙන්වන්න.
\begin{array}{rcl}&&{\begin{array}{l}\mathrm Z\;=\;\mathrm x\;+\;\mathrm{iy}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\overline{\mathrm Z}\;=\;\mathrm x\;-\;\mathrm{iy}\\\left|\mathrm Z\right|\;=\;\sqrt{\mathrm x^2\;+\;\mathrm y^2\;}\;\;\;\;\mathrm Z.\overline{\mathrm Z}\;=\;(\mathrm x\;+\;\mathrm{iy})(\mathrm x\;-\;\mathrm{iy})\\\left|\mathrm Z\right|^2\;=\;\mathrm x^2\;+\;\mathrm y^2\;\;\;\;\;\;\;\;\;\;\;\;\;=\;\;\mathrm x^2\;+\;\mathrm y^2\end{array}}\\&&{\therefore\left|\mathrm Z\right|^2\;=\;\mathrm Z.\overline{\mathrm Z}}\\&&{\begin{array}{l}\mathrm Z-\overline{\mathrm Z}\;\;=\;\mathrm x\;+\;\mathrm{iy}\;-\;\mathrm x\;+\;\mathrm{iy}\\\mathrm Z-\overline{\mathrm Z}\;=\;2\mathrm{iImZ}\end{array}}\\&&\\\left|\mathrm Z\;-\;3\mathrm i\right|^2\;&=&\;(\mathrm Z\;-\;3\mathrm i)(\overline\mathrm Z\;+\;3\mathrm i)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left|1\;+\;3\mathrm{iZ}\right|^2\;=\;(1\;-\;3\mathrm{iZ})(1\;+\;3\mathrm{i\overline Z})\\&=&\;\left|\mathrm Z\right|^2\;\;-\;6\mathrm{iZ}\;+\;9\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{=\;1\;-\;6\mathrm{iZ}\;+\;9\left|\mathrm Z\right|^2}\\&=&\;\left|\mathrm Z\right|^2\;\;-\;6\mathrm{ImZ}\;+\;9\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\;=\;1\;-\;6\mathrm{ImZ}\;+\;9\left|\mathrm Z\right|^2}\end{array}“The extension of the number concept to include the irrational ,and…the imaginary, is the greatest forward step which pure mathematics has ever taken.”
-Hermann Hankel-

