- සංයුක්ත ගණිතය I (ශුද්ධ ගණිතය) ප්රශ්න පත්රයේ B කොටසේ(රචනා ප්රශ්න) 13 වැනි ප්රශ්නයේ (a) කොටසට අඩංගු වන්නේ මෙම පාඩමේ අඩංගු සිද්ධාන්ත වේ.

1850 දී ජේම්ස් ජෝශප් සිල්වෙස්ටර් විසින් “න්යාසය” යන වචනය භාවිතා කරන ලදි. ඉංග්රීසි ගණිතඥයෙකු වන කුලිස් 1913 දී ප්රථම වරට නූතන වරහන් අංකනය භාවිතා කර ඇත. රේඛීය සමීකරණ පද්ධතියක් ලෙස හැඳින්වෙන බහු රේඛීය සමීකරණ සමඟ එකවර ලිවීමට හා වැඩ කිරීමට න්යාස භාවිතා කර ඇත.
- ගණිතමය අවයව ගොනුගත කිරීම න්යාස මගින් සිදු කරයි.
- මේ සඳහා වරහන් තුළ පේලි හා තීරු භාවිතා කරයි.
උදා:
| BOC | HNB | NSB | |
| රනිල් | 3 | 0 | -1 |
| මහින්ද | 5 | 3 | 9 |
| අනුර | \sqrt7 | 4 | -\frac53 |
| විමල් | 6 | 3 | 0 |
ඉහත සංඛ්යා පද්ධතිය තුළ පේලි 4 ක් හා තීරු 3 ක් පවතී. මෙම දත්ත සමූහය පහත පරිදි තනි න්යාසයකින් ඉදිරිපත් කළ හැකිය.
A= \begin{pmatrix}3&0&-1\\5&3&9\\\sqrt7&4&-\frac53\\6&3&0\end{pmatrix}
- න්යාසයක සාධාරණ අවයවය හඳුනා ගැනීම
a i j = i වන පේලියේ j වන අවයවය
උදා:
B=\begin{pmatrix}1&2&6\\4&-5&-3\\1&\sqrt3&\frac12\end{pmatrix}
| a 1 1 = 1 | a 1 2 = 2 | a 1 3 = 6 |
| a 2 1 = 4 | a 2 2 = -5 | a 2 3 = -3 |
| a 3 1 = 1 | a 3 2 = \sqrt3 | a 3 3 = \frac12 |
- න්යාසයක ගණය හඳුනා ගැනීම (තරම)
න්යාසයක ඝණය = පේලි ගණන × තීරු ගණන
උදා:
\begin{array}{rcl}C&=&{\begin{pmatrix}2&4\\5&3\\-2&12\end{pmatrix}}_{3\times2}\end{array}
න්යාස වර්ග හඳුනා ගැනීම
1).පේලි න්යාස
- සියලු j \in\;\mathbb{Z}^+සඳහා යම් න්යාසයක සාධාරණ අවයවය a 1 j නම් එම න්යාසය පේලි න්යාසයක් ලෙස හැඳින් වේ. (i=1)
උදා:
\begin{array}{rcl}A&=&{\begin{pmatrix}0&-1&4\end{pmatrix}}_{1\times3}\end{array} \begin{array}{rcl}B&=&{\begin{pmatrix}5&7&9&0&-4\end{pmatrix}}_{1\times5}\end{array}
- මෙම න්යාසවල එක පේලියක් පමණක් අඩංගු වන අතර ඕනෑම තීරු ගණනක් පැවතිය හැක.
2). තීරු න්යාස
- සියලු i \in\;\mathbb{Z}^+සඳහා යම් න්යාසයක සාධාරණ අවයවය a i 1 නම් එම න්යාසය තීරු න්යාසයක් ලෙස හැඳින් වේ.(j=1)
උදා:
\begin{array}{rcl}A&=&{\begin{pmatrix}0\\6\\-2\end{pmatrix}}_{3\times1}\end{array} \begin{array}{rcl}B&=&{\begin{pmatrix}4\\-1\\0\\6\\0\end{pmatrix}}_{5\times1}\end{array}
- මෙම න්යාසවල එක තීරුවක් පමණක් අඩංගු වන අතර ඕනෑම පේලි ගණනක් පැවතිය හැක.
3).ශුන්ය න්යාස
- සියලු i,j \in\;\mathbb{Z}^+සඳහා a i j =0 නම් එම න්යාසය ශුන්ය න්යාසයකි.
- එනම් න්යාසයක අවයව සියල්ලම ශුන්ය නම් එය ශුන්ය න්යාසයකි.
උදා:
\begin{array}{rcl}O&=&{\begin{pmatrix}0&0\\0&0\end{pmatrix}}_{2\times2}\end{array} \begin{array}{rcl}O&=&{\begin{pmatrix}0&0&0\\0&0&0\\0&0&0\\0&0&0\end{pmatrix}}_{4\times3}\end{array}
- ශුන්ය න්යාසය “O” මගින් සංකේතවත් කරයි.
4).සමචතුරස්ර න්යාස
- Am×n න්යාසයේ m=n නම් A සමචතුරස්ර න්යසයකි.
- එනම් මෙම න්යාස වල පේලි ගණන හා තීරු ගණන සමාන වේ.
උදා:
\begin{array}{rcl}A&=&{\begin{pmatrix}2&4\\0&3\end{pmatrix}}_{2\times2}\end{array} \begin{array}{rcl}B&=&{\begin{pmatrix}1&9&11&8\\4&2&0&3\\2&0&2&4\\4&0&0&3\end{pmatrix}}_{4\times4}\end{array}
5).විකර්ණ න්යාස
- i≠j වන විට a i j = 0 වන න්යාස විකර්ණ න්යාස නම් වේ.
උදා:
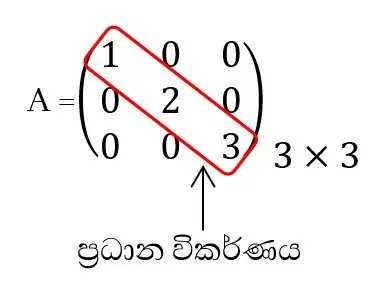
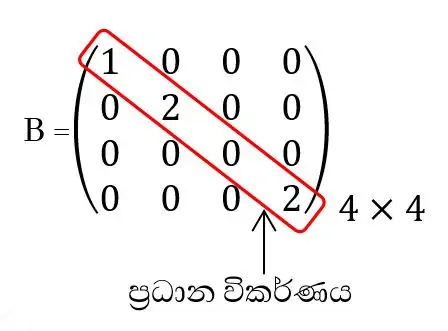
- විකර්ණ න්යාස සියල්ල සමචතුරස්ර න්යාස වේ.
6).අදිශ න්යාස
- විකර්ණ න්යාසයක විකර්නයේ අවයව එකිනෙකට සමාන නම් එය අදිශ න්යාසයකි.
උදා:
\begin{array}{rcl}A&=&{\begin{pmatrix}2&0\\0&2\end{pmatrix}}_{2\times2}\end{array} \begin{array}{rcl}B&=&{\begin{pmatrix}-1&0&0\\0&-1&0\\0&0&-1\end{pmatrix}}_{3\times3}\end{array}
7).ඒකක න්යාස
• අදිශ න්යාසයක සියලු නිශ්ශුන්ය අවයව 1 නම් එය ඒකක න්යාසයකි.
උදා:
\begin{array}{rcl}I&=&{\begin{pmatrix}1&0\\0&1\end{pmatrix}}_{2\times2}\end{array} \begin{array}{rcl}I&=&{\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}_{3\times3}\end{array}
• ඒකක න්යාසය “I” මගින් සංකේතවත් කරයි.
8).සමමිතික න්යාස
- a i j = a j i වන න්යාස සමමිතික න්යාස නම් වේ.
- එනම් ප්රධාන විකර්ණය දෙපස අවයව සමානව පවතී.
උදා:
\begin{array}{rcl}l&=&{\begin{pmatrix}2&4&1\\4&8&0\\1&0&9\end{pmatrix}}_{3\times3}\end{array}
9).කුටික සමමිතික න්යාස
- a i j = -a j i වන න්යාස කුටික සමමිතික න්යාස නම් වේ.
- ප්රධාන විකර්ණය ශුන්ය විය යුතුය.
- ප්රධාන විකර්ණය දෙපස අනුරූප අවයව විශාලත්වයෙන් සමාන හා ලකුණින් ප්රතිවිරුද්ධ විය යුතුය.
උදා:
\begin{array}{rcl}A&=&{\begin{pmatrix}0&-4&1\\4&0&-5\\-1&5&0\end{pmatrix}}_{3\times3}\end{array} \begin{array}{rcl}B&=&{\begin{pmatrix}0&-3&\frac{-5}2\\3&0&1\\\frac52&-1&0\end{pmatrix}}_{3\times3}\end{array}
10).උඩත් ත්රිකෝණ න්යාස
- ප්රධාන විකර්ණයෙන් පහළ ත්රිකෝණයේ අවයව සියල්ල ශුන්ය වන න්යාස වේ.
උදා:
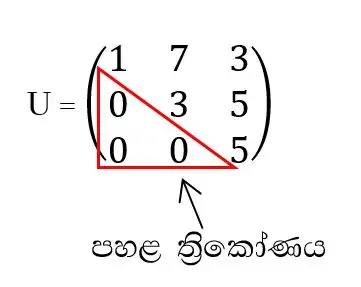
11).යටත් ත්රිකෝණ න්යාස
- ප්රධාන විකර්ණයෙන් ඉහළ ත්රිකෝණයේ අවයව සියල්ල ශුන්ය වන න්යාස වේ.
උදා:
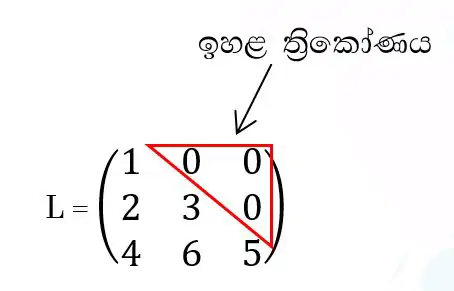
- විකර්ණ න්යාස, සමමිතික න්යාස, කුටික සමමිතික න්යාස, උඩත් ත්රිකෝණ න්යාස හා යටත් ත්රිකෝණ න්යාස යන සියල්ල සමචතුරස්ර න්යාස වේ.
න්යාස සඳහා ගණිතකර්ම
1) එකතු කිරීම හා අඩු කිරීම
- එකතු කිරීම හා අඩු කිරීම සිදු කිරිමට නම් එම න්යාසවල ඝණය සමාන විය යුතුය.
උදා:
\begin{array}{rcl}A&=&\begin{pmatrix}2&3\\4&5\end{pmatrix}\end{array} \begin{array}{rcl}B&=&\begin{pmatrix}-1&2\\5&8\end{pmatrix}\end{array} \begin{array}{rcl}C&=&\begin{pmatrix}1&-2\\3&9\\0&6\end{pmatrix}\end{array}
\begin{array}{rcl}A+B&=&\begin{pmatrix}2&3\\4&5\end{pmatrix}+\left(\begin{array}{cc}-1&2\\5&8\end{array}\right)\\&=&\begin{pmatrix}\left(2-1\right)&\left(3+2\right)\\\left(4+5\right)&\left(5+8\right)\end{pmatrix}\\&=&\begin{pmatrix}1&5\\9&13\end{pmatrix}\end{array} \begin{array}{rcl}B+A&=&\left(\begin{array}{cc}-1&2\\5&8\end{array}\right)+\begin{pmatrix}2&3\\4&5\end{pmatrix}=\begin{pmatrix}\left(-1+2\right)&\left(2+3\right)\\\left(5+4\right)&\left(8+5\right)\end{pmatrix}=\begin{pmatrix}1&5\\9&13\end{pmatrix}\\A-B&=&\begin{pmatrix}2&3\\4&5\end{pmatrix}-\begin{pmatrix}-1&2\\5&8\end{pmatrix}=\begin{pmatrix}\left(2-\left(-1\right)\right)&\left(3-2\right)\\\left(4-5\right)&\left(5-8\right)\end{pmatrix}=\begin{pmatrix}3&1\\-1&-3\end{pmatrix}\\B-A&=&\begin{pmatrix}-1&2\\5&8\end{pmatrix}-\begin{pmatrix}2&3\\4&5\end{pmatrix}=\begin{pmatrix}\left(-1-2\right)&\left(2-3\right)\\\left(5-4\right)&\left(8-5\right)\end{pmatrix}=\begin{pmatrix}-3&-1\\1&3\end{pmatrix}=\left(-1\right)\begin{pmatrix}3&1\\-1&-3\end{pmatrix}\\&=&\boldsymbol-\left(\mathbf A\boldsymbol-\mathbf B\right)\end{array}- A+C නොපවතී.
- A+B = B+A
- A – B = – (B – A)
2) න්යාසයක පෙරළුම
- A න්යාසයේ පෙරළුම AT ලෙස අංකනය කරයි.
- න්යාසයක පෙරළුම ලබා ගැනීමේදී එහි i වන පේලිය i වන තීරුව බවට පත් කළ යුතුය.
උදා:
\begin{array}{rcl}A&=&{\begin{pmatrix}2&1&3\\-1&4&2\end{pmatrix}}_{2\times3}\end{array}
\begin{array}{rcl}A^T&=&{\begin{pmatrix}2&-1\\1&4\\3&2\end{pmatrix}}_{3\times2}\end{array}
- A = AT නම්; A සමමිතික න්යාසයකි.
උදා:
\begin{array}{rcl}A&=&\begin{pmatrix}1&-4&0\\-4&2&5\\0&5&3\end{pmatrix}\\A^T&=&\begin{pmatrix}1&-4&0\\-4&2&5\\0&5&3\end{pmatrix}=A\end{array}\begin{array}{rcl}&&\therefore\end{array} A සමමිතික න්යාසයකි.
- A = -AT නම්; A කුටික සමමිතික න්යාසයකි.
උදා:
\begin{array}{rcl}A&=&\begin{pmatrix}0&1&-3\\-1&0&2\\3&-2&0\end{pmatrix}\\A^T&=&\begin{pmatrix}0&-1&3\\1&0&-2\\-3&2&0\end{pmatrix}=\left(-1\right)\begin{pmatrix}0&1&-3\\-1&0&2\\3&-2&0\end{pmatrix}=-A\end{array} \begin{array}{rcl}&&\therefore\end{array}A කුටික සමමිතික න්යාසයකි.
- (AB)T = AT.BT වේ.
- \begin{array}{rcl}\left(\lambda B\right)^T&=&\lambda.B^T\end{array}වේ.
- (A+B)T = AT+BT වේ.
උදා(1):
\begin{array}{rcl}\mathrm A&=&\begin{pmatrix}1&2\\4&3\end{pmatrix}\;\;\;\;2\mathrm A=\begin{pmatrix}2&4\\8&6\end{pmatrix}\;\;\;\;\;\;\;\;\;2.\mathrm A=2\times\begin{pmatrix}1&2\\4&3\end{pmatrix}\;\\\mathrm A^{\mathrm T}&=&\begin{pmatrix}1&4\\2&3\end{pmatrix}\;\;\;\;\left(2\;\mathrm A\right)^{\mathrm T}=\begin{pmatrix}2&8\\4&6\end{pmatrix}\;\;\;\;2.\mathrm A^{\mathrm T}=\begin{pmatrix}2&8\\4&6\end{pmatrix}\end{array}උදා(2):
\begin{array}{rcl}\mathrm A&=&\begin{pmatrix}1&2\\3&4\end{pmatrix}\;\;\;\;\;\;\;\;\;\mathrm B=\;\begin{pmatrix}5&6\\7&8\end{pmatrix}\\\mathrm A+\mathrm B&=&\begin{pmatrix}1&2\\3&4\end{pmatrix}+\begin{pmatrix}5&6\\7&8\end{pmatrix}=\begin{pmatrix}6&8\\10&12\end{pmatrix}\\\left(\mathrm A+\mathrm B\right)^{\mathrm T}&=&\begin{pmatrix}6&10\\8&12\end{pmatrix}\\\mathrm A^{\mathrm T}+\mathrm B^{\mathrm T}&=&\begin{pmatrix}1&3\\2&4\end{pmatrix}+\begin{pmatrix}5&7\\6&8\end{pmatrix}=\begin{pmatrix}6&10\\8&12\end{pmatrix}\end{array}- 2020, 2019, 2018, 2017, 2014, 2013 පසුගිය විභාග ප්රශ්න පත්රවල න්යාස පෙරළුම කොටස අඩංගු වී තිබේ.
3) 2×2 න්යාසයක නිශ්චායකයේ අගය සෙවීම
- \begin{array}{rcl}A&=&{\begin{pmatrix}a&b\\c&d\end{pmatrix}}_{2\times2}\end{array} නම්,
නිශ්චායක \begin{array}{rcl}\mathrm A&=&\det\left(\mathrm A\right)=\left|\mathrm A\right|=\mathrm{ad}-\mathrm{bc}\end{array}
උදා:
\begin{array}{rcl}\mathrm B&=&\begin{pmatrix}2&4\\5&3\end{pmatrix}\;\;,\;\left|\mathrm B\right|=\left(2\times3\right)-\left(4\times5\right)=-14\\\mathrm C&=&\begin{pmatrix}3&-1\\\frac12&\frac16\end{pmatrix}\;\;,\;\left|\mathrm C\right|=\left(3\times\frac16\right)-\left(-1\right)\frac12=1\\\mathrm D&=&\begin{pmatrix}2&2\\3&3\end{pmatrix}\;\;,\;\left|\mathrm D\right|=\left(2\times3\right)-\left(2\times3\right)=0\end{array}4) න්යාස ගුණිතය
i). න්යාසයක් අදිශයකින් ගුණ කිරීම
\begin{array}{rcl}\mathrm A&=&\begin{pmatrix}\mathrm a&\mathrm b\\\mathrm c&\mathrm d\end{pmatrix}\end{array} නම්,\begin{array}{rcl}\mathrm\lambda.\mathrm A&=&\begin{pmatrix}\mathrm{λa}&\mathrm{λb}\\\mathrm{λc}&\mathrm{λd}\end{pmatrix}\end{array}
උදා:\begin{array}{rcl}\mathrm B&=&\begin{pmatrix}2&4\\0&3\end{pmatrix}\end{array} නම්,
\begin{array}{rcl}2\mathrm B&=&\begin{pmatrix}4&8\\0&6\end{pmatrix}\\\left(-\frac12\right)\mathrm B&=&\begin{pmatrix}-1&-2\\0&-\frac32\end{pmatrix}\end{array}
ii)න්යාසයක් තවත් න්යාසයකින් ගුණ කිරීම
න්යාසයක් තවත් න්යාසයකින් ගුණ කිරීමට අවශ්යතාවය:
පළමු න්යාසයේ තීරු ගණන = දෙවන න්යාසයේ පේලි ගණන
උදා:\mathrm A={\begin{pmatrix}4&2\\3&-1\end{pmatrix}}_{2\times2} , \mathrm B={\begin{pmatrix}5&-2&3\\6&1&-1\end{pmatrix}}_{2\times3} ,\mathrm C={\begin{pmatrix}3&2\\1&0\\-2&-1\end{pmatrix}}_{3\times2}
A B ගුණිතය පවතී.
B C ගුණිතය පවතී.
B A ගුණිතය නොපවතී.
A C ගුණිතය නොපවතී.
- ගුණ කරන පිළිවෙල (දිශාව) ඉතා වැදගත් වේ. එනම්;
AB යනු A න්යාසයෙන් B න්යාසය ගුණ කිරීම වේ.
BA යනු B න්යාසයෙන් A න්යාසය ගුණ කිරීම වේ.
- න්යාස දෙකක් ගුණ කිරීමෙන් තවත් න්යාසයක් ම ලැබේ.
- නව න්යාසයේ “ඝණය = පළමු න්යාසයේ පේලි ගණන × දෙවන න්යාසයේ තීරු ගණන” වේ.
\mathrm A={\begin{pmatrix}\mathrm a&\mathrm b&\mathrm c\\\mathrm d&\mathrm e&\mathrm f\end{pmatrix}}_{2\times3} \mathrm B={\begin{pmatrix}\mathrm g&\mathrm j\\\mathrm h&\mathrm k\\\mathrm i&\mathrm l\end{pmatrix}}_{3\times2}
1. AB න්යාසයේ ගණය = 2×2 විය යුතුය.
\mathrm{AB}=\begin{pmatrix}\mathrm a&\mathrm b&\mathrm c\\\mathrm d&\mathrm e&\mathrm f\end{pmatrix}\begin{pmatrix}\mathrm g&\mathrm j\\\mathrm h&\mathrm k\\\mathrm i&\mathrm l\end{pmatrix}={\begin{pmatrix}\left(\mathrm{ag}+\mathrm{bh}+\mathrm{ci}\right)&\left(\mathrm{aj}+\mathrm{bk}+\mathrm{cl}\right)\\\left(\mathrm{dg}+\mathrm{eh}+\mathrm{fi}\right)&\left(\mathrm{dj}+\mathrm{ek}+\mathrm{fl}\right)\end{pmatrix}}_{2\times2}2. BA න්යාසයේ ගණය = 3×3 විය යුතුය.
\mathrm{BA}=\begin{pmatrix}\mathrm g&\mathrm j\\\mathrm h&\mathrm k\\\mathrm i&\mathrm l\end{pmatrix}\begin{pmatrix}\mathrm a&\mathrm b&\mathrm c\\\mathrm d&\mathrm e&\mathrm f\end{pmatrix}={\begin{pmatrix}\left(\mathrm{ga}+\mathrm{jd}\right)&\left(\mathrm{gb}+\mathrm{je}\right)&\left(\mathrm{jc}+\mathrm{jf}\right)\\\left(\mathrm{ha}+\mathrm{kd}\right)&\left(\mathrm{hb}+\mathrm{ke}\right)&\left(\mathrm{hc}+\mathrm{kf}\right)\\\left(\mathrm{ia}+\mathrm{ld}\right)&\left(\mathrm{ib}+\mathrm{le}\right)&\left(\mathrm{ic}+\mathrm{lf}\right)\end{pmatrix}}_{3\times3}- බොහෝ විට AB≠BAවේ.
උදා:
\begin{array}{rcl}\mathrm A&=&\begin{pmatrix}2&3\\4&5\end{pmatrix}\;\mathrm B=\begin{pmatrix}-3&1\\2&-2\end{pmatrix}\\\mathrm{AB}&=&\begin{pmatrix}2&3\\4&5\end{pmatrix}\times\begin{pmatrix}-3&1\\2&-2\end{pmatrix}=\begin{pmatrix}\left(2\left(-3\right)+3\times2\right)&\left(2\times1+3\left(-2\right)\right)\\\left(4\left(-3\right)+5\times2\right)&\left(4\times1+5\times\left(-2\right)\right)\end{pmatrix}=\begin{pmatrix}0&-4\\-2&-6\end{pmatrix}\end{array} \begin{array}{rcl}\mathrm{AB}&=&\begin{pmatrix}-3&1\\2&-2\end{pmatrix}\times\begin{pmatrix}2&3\\4&5\end{pmatrix}=\begin{pmatrix}\left(\left(-3\right)2+1\times4\right)&\left(\left(-3\right)3+1\times5\right)\\\left(2\times2+\left(-2\right)4\right)&\left(2\times3+\left(-2\right)5\right)\end{pmatrix}=\begin{pmatrix}-2&-4\\-4&-4\end{pmatrix}\end{array}\begin{array}{rcl}\therefore\end{array} AB≠BA
- \;\mathrm\lambda\;\mathrm{අදිශයක්}\;\mathrm{විට}\;,\;\;\mathrm\lambda\;\mathrm{AB}\;=(\mathrm\lambda\;\mathrm A)\mathrm B=\;\mathrm A\;(\mathrm\lambda\;\mathrm B)=\mathrm\lambda\;(\mathrm{AB})
උදා:
\begin{array}{rcl}\mathrm A&=&\begin{pmatrix}2&3\\4&5\end{pmatrix}\;\mathrm B=\begin{pmatrix}-3&1\\2&-2\end{pmatrix}\\\mathrm{AB}&=&\begin{pmatrix}2&3\\4&5\end{pmatrix}\times\begin{pmatrix}-3&1\\2&-2\end{pmatrix}=\begin{pmatrix}0&-4\\-2&-6\end{pmatrix}\\2\mathrm{AB}&=&2\begin{pmatrix}2&3\\4&5\end{pmatrix}\times\begin{pmatrix}-3&1\\2&-2\end{pmatrix}=\begin{pmatrix}0&-8\\-4&-12\end{pmatrix}\\\left(2\mathrm A\right)\mathrm B&=&\begin{pmatrix}4&6\\8&10\end{pmatrix}\times\begin{pmatrix}-3&1\\2&-2\end{pmatrix}=\begin{pmatrix}0&-8\\-4&-12\end{pmatrix}\\2\left(\mathrm{AB}\right)&=&2\left[\begin{pmatrix}2&3\\4&5\end{pmatrix}\times\begin{pmatrix}-3&1\\2&-2\end{pmatrix}\right]=2\times\begin{pmatrix}0&-4\\-2&-6\end{pmatrix}=\begin{pmatrix}0&-8\\-4&-12\end{pmatrix}\\\therefore2\mathrm{AB}&=&\left(2\mathrm A\right)\mathrm B=\mathrm A\left(2\mathrm B\right)=2\left(\mathrm{AB}\right)\end{array}- An+m =An . Am
උදා:
\begin{array}{rcl}\mathrm A&=&\begin{pmatrix}2&-1\\0&3\end{pmatrix}\end{array}
\begin{array}{rcl}1.\;\;\mathrm A^2&=&\mathrm A^{1+1}\\&=&\mathrm A^1.\mathrm A^1\\&=&\begin{pmatrix}2&-1\\0&3\end{pmatrix}\;\begin{pmatrix}2&-1\\0&3\end{pmatrix}\\&=&\begin{pmatrix}4&-5\\0&9\end{pmatrix}\\2.\;\;\mathrm A^3&=&\mathrm A^{2+1}\\&=&\mathrm A^2.\mathrm A^1\\&=&\begin{pmatrix}4&-5\\0&9\end{pmatrix}\begin{pmatrix}2&-1\\0&3\end{pmatrix}\\&=&\begin{pmatrix}8&-19\\0&27\end{pmatrix}\end{array}
- (A+B)2 =A2 + A.B + B.A + B2
උදා:
\begin{array}{rcl}\mathrm A&=&\begin{pmatrix}0&-1\\2&4\end{pmatrix}\;\;\;\;\mathrm B=\begin{pmatrix}-1&3\\0&2\end{pmatrix}\end{array}
\begin{array}{rcl}\left(\mathrm A+\mathrm B\right)^2&=&\left[\begin{pmatrix}0&-1\\2&4\end{pmatrix}+\begin{pmatrix}-1&3\\0&2\end{pmatrix}\right]^2\\&=&\begin{bmatrix}-1&2\\2&6\end{bmatrix}^2\\&=&\begin{pmatrix}-1&2\\2&6\end{pmatrix}\begin{pmatrix}-1&2\\2&6\end{pmatrix}=\begin{pmatrix}5&10\\10&40\end{pmatrix}\end{array}A2 + A.B + B.A + B2
\begin{array}{rcl}&=&\begin{pmatrix}0&-1\\2&4\end{pmatrix}\begin{pmatrix}0&-1\\2&4\end{pmatrix}+\begin{pmatrix}0&-1\\2&4\end{pmatrix}\begin{pmatrix}-1&3\\0&2\end{pmatrix}+\begin{pmatrix}-1&3\\0&2\end{pmatrix}\begin{pmatrix}0&-1\\2&4\end{pmatrix}+\begin{pmatrix}-1&3\\0&2\end{pmatrix}\begin{pmatrix}-1&3\\0&2\end{pmatrix}\\&=&\begin{pmatrix}-2&-4\\8&14\end{pmatrix}+\begin{pmatrix}0&-2\\-2&14\end{pmatrix}+\begin{pmatrix}6&13\\4&8\end{pmatrix}+\begin{pmatrix}1&3\\0&4\end{pmatrix}\\&=&\begin{pmatrix}5&10\\10&40\end{pmatrix}\end{array}- AI = IA = A
උදා:
\begin{array}{rcl}&&\mathrm A\end{array}\begin{array}{rcl}&=&\end{array}\begin{array}{rcl}&&\begin{pmatrix}2&0\\3&1\end{pmatrix}\end{array} \begin{array}{l}\mathrm{AI}=\begin{pmatrix}2&0\\3&1\end{pmatrix}\begin{pmatrix}1&0\\0&1\end{pmatrix}=\begin{pmatrix}2&0\\3&1\end{pmatrix}\\\mathrm{IA}=\begin{pmatrix}1&0\\0&1\end{pmatrix}\begin{pmatrix}2&0\\3&1\end{pmatrix}=\begin{pmatrix}2&0\\3&1\end{pmatrix}\end{array}- AB + AC = A [IB + IC] = A [B + C]
- BA + CA = [B + C] A
- \mathrm\lambdaA + BA = [\mathrm\lambdaI + B] A
- BA + AC ≠ [B +C] A ≠ A[B+C]
උදා:
\begin{array}{rcl}\mathrm A=\begin{pmatrix}0&1\\-1&2\end{pmatrix}\;\;\;\mathrm B=\begin{pmatrix}1&2\\3&4\end{pmatrix}\;\;\mathrm C=\begin{pmatrix}2&3\\-1&0\end{pmatrix}\end{array} \begin{array}{rcl}\mathrm{AB}+\mathrm{AC}&=&\begin{pmatrix}0&1\\-1&2\end{pmatrix}\begin{pmatrix}1&2\\3&4\end{pmatrix}+\begin{pmatrix}0&1\\-1&2\end{pmatrix}\begin{pmatrix}2&3\\-1&0\end{pmatrix}\\&=&\begin{pmatrix}3&4\\5&6\end{pmatrix}+\begin{pmatrix}-1&0\\-4&-3\end{pmatrix}\\&=&\begin{pmatrix}2&4\\1&3\end{pmatrix}\\\mathrm{BA}+\mathrm{CA}&=&\begin{pmatrix}1&2\\3&4\end{pmatrix}\;\begin{pmatrix}0&1\\-1&2\end{pmatrix}+\begin{pmatrix}2&3\\-1&0\end{pmatrix}\;\begin{pmatrix}0&1\\-1&2\end{pmatrix}\\&=&\begin{pmatrix}-2&5\\-4&11\end{pmatrix}+\begin{pmatrix}-3&8\\0&-1\end{pmatrix}\\&=&\begin{pmatrix}-5&13\\-4&10\end{pmatrix}\\\left(\mathrm B+\mathrm C\right)\mathrm A&=&\left[\begin{pmatrix}1&2\\3&4\end{pmatrix}+\begin{pmatrix}2&3\\-1&0\end{pmatrix}\right]\;\begin{pmatrix}0&1\\-1&2\end{pmatrix}\\&=&\begin{pmatrix}3&5\\2&4\end{pmatrix}\begin{pmatrix}0&1\\-1&2\end{pmatrix}\\&=&\begin{pmatrix}-5&13\\-4&10\end{pmatrix}\end{array}
\thereforeBA+CA=(B+C)A
\begin{array}{rcl}\mathrm{BA}+\mathrm{AC}&=&\begin{pmatrix}1&2\\3&4\end{pmatrix}\begin{pmatrix}0&1\\-1&2\end{pmatrix}+\begin{pmatrix}0&1\\-1&2\end{pmatrix}\begin{pmatrix}2&3\\-1&0\end{pmatrix}\\&=&\begin{pmatrix}-2&5\\-4&11\end{pmatrix}\begin{pmatrix}-1&0\\-4&-3\end{pmatrix}\\&=&\begin{pmatrix}-3&5\\-8&8\end{pmatrix}\end{array}\thereforeBA+AC ≠ (B+C)A ≠ A(B+C)
\begin{array}{rcl}2\mathrm A+\mathrm{BA}&=&2\begin{pmatrix}0&1\\-1&2\end{pmatrix}+\begin{pmatrix}1&2\\3&4\end{pmatrix}\begin{pmatrix}0&1\\-1&2\end{pmatrix}\\&=&\begin{pmatrix}0&2\\-2&4\end{pmatrix}+\begin{pmatrix}-2&5\\-4&11\end{pmatrix}\\&=&\begin{pmatrix}-2&7\\-6&15\end{pmatrix}\\\left[2\mathrm I+\mathrm B\right]\;\mathrm A&=&\left[2\begin{pmatrix}1&0\\0&1\end{pmatrix}+\begin{pmatrix}1&2\\3&4\end{pmatrix}\right]\begin{pmatrix}0&1\\-1&2\end{pmatrix}\\&=&\begin{pmatrix}3&2\\3&6\end{pmatrix}\begin{pmatrix}0&1\\-1&2\end{pmatrix}\\\therefore2\mathrm A+\mathrm{BA}&=&\left[2\mathrm I+\mathrm B\right]\;\mathrm A\end{array}5) සම්බන්ධ න්යාසය ( 2×2 න්යාස සදහා පමණි)
\begin{array}{rcl}\mathrm A&=&\begin{pmatrix}\mathrm x&\mathrm y\\\mathrm z&\mathrm w\end{pmatrix}\;\;\;\mathrm{නම්},\;\;\;\;\mathrm{adj}\;\mathrm A=\begin{pmatrix}\mathrm w&-\mathrm y\\-\mathrm z&\mathrm x\end{pmatrix}\\\mathrm{උදා}:\mathrm B&=&\begin{pmatrix}2&4\\3&5\end{pmatrix}\;\;\;\mathrm{නම්},\;\;\;\;\mathrm{adj}\;\mathrm B=\begin{pmatrix}5&-3\\-4&2\end{pmatrix}\end{array}6) ප්රතිලෝම න්යාසය සෙවීම
- A න්යාසයේ ප්රතිලෝම න්යාසය A-1 ලෙස අංකනය කරයි.
- ප්රතිලෝම න්යාසයක් පැවතීමට අවශ්යතාවය ;
නිශ්චායකයේ අගය (|A|)≠0 වීමයි.
උදා:
\begin{array}{rcl}\mathrm i).\;\;\mathrm A&=&\begin{pmatrix}2&1\\3&4\end{pmatrix}\;\;\;\;\;\;\vert\mathrm A\vert\;=(2\times4)-(1\times3)=5\;\;\;\;\;\;\;\;\;\mathrm A^{-1}\;\;\mathrm{පවතී}.\;\\\;\;\mathrm{ii}).\;\mathrm B&=&\begin{pmatrix}3&-2\\3&-1\end{pmatrix}\;\;\;\;\;\vert\mathrm B\vert\;=2(-1)-(-2)3=-8\;\;\;\;\;\mathrm B^{-1}\;\;\mathrm{පවතී}.\;\\\mathrm{iii}).\;\mathrm C&=&\begin{pmatrix}2&1\\-2&-1\end{pmatrix}\;\;\;\vert\mathrm C\vert\;=2(-1)-(-2)1=0\;\;\;\;\;\;\;\;\;\mathrm C^{-1}\;\;\mathrm{නොපවතී}.\\&&\end{array}- 2020, 2019, 2014 පසුගිය විභාග ප්රශ්න වලදී ඉහත යෙදීම අවශ්ය වේ
- ප්රතිලෝම න්යාස සොයන ආකාර දෙකකි.
i).සූත්ර භාවිතයෙන්
- මෙම ක්රමයෙන් ඍජුව ප්රතිලෝම න්යාසය ලැබේ.
\begin{array}{rcl}\mathrm A^{-1}&=&\frac1{\left|\mathrm A\right|}.\mathrm{adj}\;\mathrm A\end{array}
\begin{array}{rcl}\mathrm{උදා}:\;\;\mathrm A&=&\begin{pmatrix}2&1\\3&4\end{pmatrix}\\\mathrm A^{-1}&=&\frac1{\left(2\times4-1\times3\right)}.\begin{pmatrix}4&-1\\-3&2\end{pmatrix}=\frac15\begin{pmatrix}4&-1\\-3&2\end{pmatrix}=\begin{pmatrix}\frac45&-\frac15\\-\frac35&\frac25\end{pmatrix}\end{array}- ප්රතිලෝම න්යාසය ලියා දැක්වීමට කියා ඇත්නම් පමණක් මෙම ක්රමය භාවිතා කළ හැක.
- 2020, 2019, 2018, 2017 පසුගිය විභාග ප්රශ්න පත්රවල ප්රතිලෝම න්යාසය “ලියා දක්වන්න” යැයි සදහන් අවස්ථාවල මෙම ක්රමයෙන් ඍජුව ප්රතිලෝම න්යාසය ලබාගෙන පිළිතුරු පත්රයේ ලිවිය හැක.
ii).වීජීය ක්රමයෙන්
- A.A-1 = A-1.A = I
\begin{array}{rcl}\begin{pmatrix}2&3\\6&4\end{pmatrix}\begin{pmatrix}\mathrm a&\mathrm b\\\mathrm c&\mathrm d\end{pmatrix}&=&\begin{pmatrix}1&0\\0&1\end{pmatrix}\\\begin{array}{c}\begin{pmatrix}\left(2\mathrm a+3\mathrm c\right)&\left(2\mathrm b+3\mathrm d\right)\\\left(6\mathrm a+4\mathrm c\right)&\left(6\mathrm b+4\mathrm d\right)\end{pmatrix}\end{array}&=&\begin{pmatrix}1&0\\0&1\end{pmatrix}\\&&\\&&\end{array}
\begin{array}{rcl}(2a+3c)&=&1\;\rightarrow(1)\\(2b+3d)&=&0\;\rightarrow(2)\\(6a+4c)&=&0\;\rightarrow{(3)}\\(6b+4d)&=&1\;\rightarrow{(4)}\end{array}ඉහත සමීකරණ විසඳා a, b, c, d සොයා ප්රතිලෝම න්යාසය ලබාගත හැක.
\begin{array}{rcl}\mathrm{උදා}:\;\;\;\mathrm A&=&\begin{pmatrix}4&2\\3&1\end{pmatrix}\;\;\;,\;\;\;\;\mathrm A^2-5\mathrm A-2\mathrm I\;=0\;\;\mathrm{නම්}\;\;\;\;\mathrm A^{-1}\;\;\mathrm{සොයන්න}.\end{array}\begin{array}{rcl}\mathrm A^2-5\mathrm A-2\mathrm I\;&=&0\\\mathrm A^2-5\mathrm A&=&2\mathrm I\\\mathrm A\left(\mathrm A-5\mathrm I\right)&=&2\mathrm I\\\mathrm A\times\frac12\left(\mathrm A-5\mathrm I\right)&=&\mathrm I\end{array}
\begin{array}{rcl}\mathrm A\times\mathrm A^{-1}&=&\mathrm I\;\mathrm{අනුව},\\\;\mathrm A^{-1}&=&\frac12\left(\mathrm A-5\mathrm I\right)\\\mathrm A^{-1}&=&\frac12\left[\begin{pmatrix}4&2\\3&1\end{pmatrix}-5\begin{pmatrix}1&0\\0&1\end{pmatrix}\right]\\&=&\frac12\begin{bmatrix}-1&2\\3&-4\end{bmatrix}\\&&\end{array}- 2011, 2012, 2013, 2016 පසුගිය විභාග ප්රශ්නවල ඉහත ආකාරයේ ප්රකාශන භාවිතයෙන් ප්රතිලෝම න්යාසය අපෝහනය කිරීමට ඇත.
- (AB)-1 = B-1. A-1 වේ.
- \left(\mathrm{λA}\right)^{-1}=\frac1{\mathrm\lambda}\mathrm A^{-1}
7) න්යාස භාවිතයෙන් සමගාමී සමීකරණ විසඳීම
\begin{array}{l}{\mathrm a}_1\mathrm x+{\mathrm b}_1\mathrm y={\mathrm c}_1\\{\mathrm a}_2\mathrm x+{\mathrm b}_2\mathrm y={\mathrm c}_2\;\;\;\;,\;\mathrm{නම්}\;\;\;\mathrm x,\mathrm y\;\mathrm{සොයන්න}.\\\mathrm A=\begin{pmatrix}{\mathrm a}_1&{\mathrm b}_1\\{\mathrm a}_2&{\mathrm b}_2\end{pmatrix}\;,\;\;\;\;\mathrm X=\begin{pmatrix}\mathrm x\\\mathrm y\end{pmatrix}\;,\;\;\;\;\mathrm C=\begin{pmatrix}{\mathrm c}_1\\{\mathrm c}_2\end{pmatrix}\;\;\;\;,\mathrm{ලෙස}\;\mathrm{ගමු}.\end{array} \begin{array}{rcl}\mathrm{AX}&=&\mathrm C\\\mathrm A-1\;\;\;\mathrm{පවතින}\;\mathrm{විට},\;\;\;\;\mathrm A^{-1}.\;\mathrm{AX}&=&\mathrm A^{-1}\mathrm C\;\\\mathrm{IX}&=&\mathrm A^{-1}\mathrm C\\\mathrm X&=&\mathrm A^{-1}\mathrm C\end{array}උදා:
\begin{array}{rcl}2\mathrm x+\mathrm y&=&4\\3\mathrm x-\mathrm y&=&0\;\;\;\;,\;\mathrm{නම්}\;\;\;\operatorname{𝑥},\operatorname{𝑦}\;\mathrm{සොයන්න}\end{array} \mathrm A=\begin{pmatrix}2&1\\3&-1\end{pmatrix}\;,\;\;\;\;\mathrm X=\begin{pmatrix}\mathrm x\\\mathrm y\end{pmatrix}\;,\;\;\;\;\mathrm C=\begin{pmatrix}4\\0\end{pmatrix}\;,\;\mathrm{ලෙස}\;\mathrm{ගමු}. \mathrm A^{-1}=\frac1{-2-3}\begin{pmatrix}-1&-1\\-3&2\end{pmatrix}=-\frac15\begin{pmatrix}-1&-1\\-3&2\end{pmatrix} \begin{array}{rcl}\mathrm{AX}&=&\mathrm C\\\mathrm A^{-1}.\mathrm{AX}&=&\mathrm A^{-1}\mathrm C\\\mathrm{IX}&=&\mathrm A^{-1}\mathrm C\\\mathrm X&=&\mathrm A^{-1}\mathrm C\\\begin{pmatrix}\mathrm x\\\mathrm y\end{pmatrix}&=&-\frac15\begin{pmatrix}-1&-1\\-3&2\end{pmatrix}\begin{pmatrix}4\\0\end{pmatrix}\\\begin{pmatrix}\mathrm x\\\mathrm y\end{pmatrix}&=&-\frac15\begin{pmatrix}-4\\-12\end{pmatrix}=\begin{pmatrix}\frac45\\\frac{12}5\end{pmatrix}\\\mathrm x&=&\frac45\\\mathrm y&=&\frac{12}5\end{array}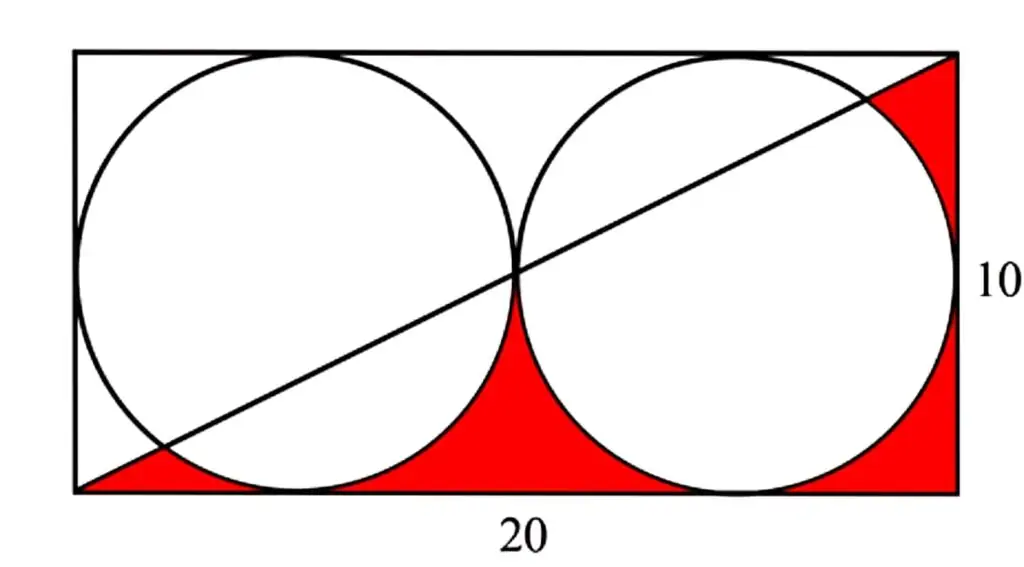
සෘජුකෝණාස්රයේ දිග ඒකක 20ක් ද පළල ඒකක 10 ක් ද බව සලකා රතු පාටින් අඳුරු කර ඇති කොටසේ මුලු වර්ගඵලය සොයන්න.
- අභ්යාස-
(i)A=\begin{pmatrix}7&8\\-6&-7\end{pmatrix} වන විට, A^2සොයා, ඒ නයින්,A^{-1}ලබාගන්න.A^{2015}X=\begin{pmatrix}1&-1\\1&2\end{pmatrix} වන පරිදි X න්යාසය නිර්ණය කරන්න.
\begin{array}{rcl}A&=&\begin{pmatrix}7&8\\-6&-7\end{pmatrix}\\A^2&=&\begin{pmatrix}7&8\\-6&-7\end{pmatrix}\begin{pmatrix}7&8\\-6&-7\end{pmatrix}\;\;\;\;\;\;\;\;\;(5)\\&=&\begin{pmatrix}1&0\\0&1\end{pmatrix}=I\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{(5)}\\\therefore A^{-1}&=&A\text{වේ.}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{(5)}\;\;\;\;\;\;\;\;\lbrack15\rbrack\\A^{2015}X&=&\begin{pmatrix}1&-1\\1&2\end{pmatrix}\\\left(A^2\right)^{1007}AX&=&\begin{pmatrix}1&-1\\1&2\end{pmatrix}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{(5)}\\I\;AX&=&\begin{pmatrix}1&-1\\1&2\end{pmatrix}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\;\;\;\;(5)}\\A^{-1}\;AX&=&\begin{pmatrix}7&8\\-6&-7\end{pmatrix}\begin{pmatrix}1&-1\\1&2\end{pmatrix}\;\;\;\;\;\;\;\;\;\;\;\;\;{(5)}+(5)\\X&=&\begin{pmatrix}15&9\\-13&-8\end{pmatrix}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{(5)}{\;\;\;\;\;\;\;\;\;\lbrack15\rbrack}\\&&\\&&\end{array}“The folly of mistaking a paradox for a discovery, a metaphor for a proof, a torrent of verbiage for a spring of capital truths, and oneself for an oracle, is inborn in us.”
-Paul Valery

