- සිරස් වෘත්ත චලිතයේ යෙදෙන අංශුවක ස්පර්ශීය ප්රවේගයේ දිශාව මෙන්ම විශාලත්වයද වෙනස් විය හැකිය.
- ∴ එම අංශුව විචල්ය ස්පර්ශීය ප්රවේගයකින් වෘත්ත චලිතයේ යෙදෙන අංශුවක් වන නිසා ආරම්භක අවස්ථාව හා චලිතයේ සාධාරණ අවස්ථාවක් සලකා ශක්ති සංස්ථිති මූලධර්මය හා වෘත්තයේ කේන්ද්රය දෙසට F = ma සමීකරණය යෙදීම මගින් අවශ්ය කරුණු සොයා එම ගැටලුව විසදිය හැක.
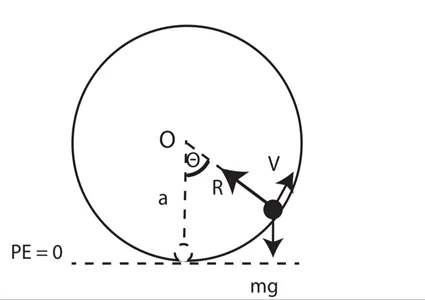
උදා: කේන්ද්රය O හා අරය a වන අචල ගෝලයක මුදුනෙහි ස්කන්ධය m වන P අංශුවක් නිශ්චලතාවයෙන් ඇත. එය සමතුලිතතා පිහිටීමෙන් සීරුවෙන් විස්ථාපනය කරයි. OP රේඛාව උඩු අත් සිරස සමඟ θ කෝණයක් සාදන විට\overset.{\theta^2}=(1+cosθ) බව පෙන්වන්න.
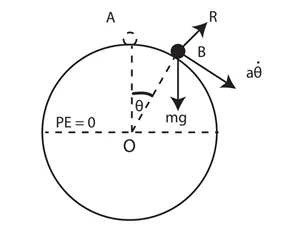
PE=0 යනු විභව ශක්තිය ශුන්ය යැයි උපකල්පනය කරනු ලබන මට්ටම වේ.
ශක්ති සංස්ථිති මූලධර්මයෙන්,
A හිදී ශක්තිය = B හිදී ශක්තිය
mga+0=mgacosθ+½m(a\overset.\theta)2
g=gcosα+½a\overset.{\theta^2}
g(1-cosθ)=½a\overset.{\theta^2}
\overset.{\theta^2}=\frac{2g}a(1+cosθ)
විචල්ය ස්පර්ශීය ප්රවේගයකින් වෘත්ත චලිතයේ යෙදෙන අංශුවක ත්වරණය සෙවීම.
- කේන්ද්රය O හා අරය r වු වෘත්තයක පරිධිය මත P ලක්ෂ්යයක ඇති අංශුවක් t කාලයකදී θ කෝණික විස්ථාපනයක් සහිතව A ලක්ෂ්යයටද නැවත δt කාලයකට පසු δθ කෝණික විස්ථාපනයක් සහිතව B ලක්ෂ්යයටද ගමන් කරන්නේ යැයි සිතමු.
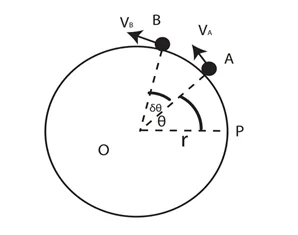
01. කේන්ද්රය දෙසට ත්වරණය සෙවීම.
\begin{array}{rcl}A\;\text{හිදී කේන්ද්රය දෙසට ප්රවේගය}&=&0\\B\text{හිදී AO දිශාවට ප්රවේගය}&=&(V+\delta V)sin\delta\theta\delta\\\text{t කාලය තුළ කේන්ද්රය දෙසට ප්රවේග වෙනස}&=&(V+\delta V)sin\delta\theta-0\\&=&(V+\delta V)sin\delta\theta\\\text{∴ඒකීය කාලයකදී කේන්ද්රය දෙසට ප්රවේග වෙනස}&=&(V+\delta V)sin\left(\frac{\delta\theta}{\delta t}\right)\\\text{∴ A හිදී කේන්ද්රය දෙසට ත්වරණය}&=&\lim_{\delta t\rightarrow0\;}\;\frac{(V+\delta V)sin\delta\theta}{\delta\theta}\\&=&\lim_{\delta t\rightarrow0\;}(V+\delta V)\times\lim_{\delta t\rightarrow0\;}\frac{sin\delta\theta}{\delta\theta}\times\lim_{\delta t\rightarrow0\;}\frac{\delta\theta}{\delta t}\\&=&v\times1\times\dot\theta\\&=&v\dot\theta\\&&\\&&\end{array}
\begin{array}{rcl}a&=&V\dot\theta\\a&=&\frac{V^2}r\\a&=&r\dot\theta{}^2\end{array}
02. ස්පර්ශීය දිශාවට ත්වරණය සෙවීම.
\begin{array}{rcl}\mathrm A\;\mathrm{හිදී}\;\mathrm{ස්පර්ශීය}\;\mathrm{දිශාවට}\;\mathrm{ප්}\mathrm{රවේගය}&=&V\\text{B හිදී A හි ස්පර්ශීය දිශාවට ප්රවේගය}&=&(V+\delta V)cos\delta\theta\;\\\text{δt කාලයක් තුළ ප්රවේග වෙනස්වීම}&=&(V+\delta V)cos\delta\theta-V\\\therefore\;\text{ඒකක කාලයකදී ප්රවේග වෙනස්වීම}&=&\frac{\lbrack(V+\delta V)\cos\delta\theta-V\rbrack}{\delta t}\\\text{∴A හිදී ස්පර්ශීය දිශාවට ත්වරණය}&=&\lim_{\delta t\rightarrow0}\;\;\frac{(V+\delta V)\cos\delta\theta-V}{\delta t}\\&=&\lim_{\delta t\rightarrow0}\frac{(V+\delta V)\cos\delta\theta}{\delta t}\;-\;\lim_{\delta t\rightarrow0}\frac V{\delta t}\\&=&\lim_{\delta t\rightarrow0\;}\frac{V\cos\delta\theta-v}{\delta t}\;+\lim_{\delta t\rightarrow0\;}\frac{\delta V\cos\delta\theta}{\delta t}\\&=&\lim_{\delta t\rightarrow0\;}\frac{V(\cos\delta\theta-1)}{\delta t}\;+\;\frac{dv}{dt}\\&=&\frac{-2v}2\times\lim_{\frac{\delta t}2\rightarrow0\;}\sin\frac{\left({\displaystyle\frac{\delta\theta}2}\right)}{\frac{\delta t}2}\times\lim_{\frac{\delta t}2\rightarrow0\;}\sin\frac{\delta t}2\times\frac{\delta\theta}{\delta t}+\frac{dv}{dt}\\&=&0\;+\;\frac{dv}{dt}\\&=&\frac{dv}{dt}\\&=&r\ddot\theta\\&&\end{array}
සිරස් වෘත්ත චලිතය හා සම්බන්ධ ගැටලු ආකාර.
- සිරස් වෘත්ත චලිතය ගැන සාකච්ඡා කිරීමේදී අපහට ගැටලු ආකාර කිහිපයක් හමුවේ.
- ඒවා නම්,
- සුමට ගෝලීය පෘෂ්ඨයක් මත අංශුවක වෘත්ත චලිතය.
- සුමට කුහර ගෝලයක් ඇතුළත අංශුවක වෘත්ත චලිතය.
- ලුහු අවිතන්ය තන්තුවක් මගින් අචල ලක්ෂ්යයකට සම්බන්ධ කර ඇති අංශුවක සිරස් වෘත්ත චලිතය.
- සිරස් නළයක් තුළ අංශුවක චලිතය.
ඉහත ගැටලු ආකාර පිළිබඳව උදාහරණ ගැටලු සහිතව සාකච්ඡා කරමු.
01. සුමට ගෝලීය පෘෂ්ඨයක් මත අංශුවක වෘත්ත චලිතය.
(2007 A/L)
උදා:
i. O කේන්ද්රය හා a අරය සහිත සුමට ගෝලයක්, මේසයක තිරස් පෘෂ්ඨය මතට සවි කර ඇත. සුමට P අංශුවක් ගෝලයෙහි පිටත පෘෂ්ඨයෙහි A ලක්ෂ්යයක තබයි. මෙහි OA, උඩු සිරස සමඟ α සුළු කෝණයක් සාදයි. අංශුව නිශ්චලතාවයෙන් මුදා හරියි.
ii. OP උඩු සිරස සමඟ θ කෝණයක් සාදන විට, අංශුව තවමත් ගෝල පෘෂ්ඨය සමඟ ස්පර්ශ වී ඇත්නම් \begin{array}{rcl}a\dot\theta^2&=&\;2g\;(\cos\;\alpha\;-\;\cos\;\theta)\end{array}බව පෙන්වන්න.
iii. ගෝලය හා අංශුව අතර ප්රතික්රියාවේ විශාලත්වය සොයන්න.
iv. මේසයේ පෘෂ්ඨයේ සිට a (1 + ⅔ cos α) උසකදී අංශුව ගෝලයෙන් ඉවත්ව යන බව පෙන්වන්න.
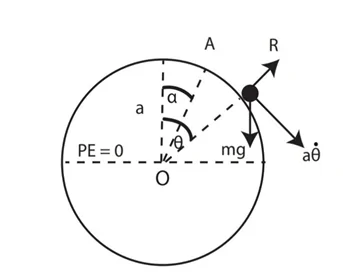
i. ශක්ති සංස්ථිති නියමයෙන්,
A හි ශක්තිය = B හි ශක්තිය
mga cos α + ½ × m × 0 = mga cos θ + ½ × m × v2
ga cos α + 0 = ga cos θ + ½ (a\overset.\theta)2
g cos α = g cos θ + ½ a\overset.\theta^2
a\overset.\theta^2= 2g (cos α – cos θ) ————(1)
ii. m අංශුවට B හිදී,
F = ma
mg cos θ – R = ma\overset.\theta^2
R = mg cos θ – ma\overset.\theta^2
R = mg cos θ – m × 2g (cos α – cos θ) ; ඉහත (1) ප්රකාශනයට අනුව
R = mg (3 cosθ – 2 cos α)
iii. අංශුව මේසයෙන් ඉවත් වෙයි නම්, R = 0 වේ. තවද,
R = mg (3 cosθ – 2 cos α)
mg (3 cosθ – 2 cos α) = 0
3 cosθ = 2 cos α
cos θ = ⅔ cos α———-(2)
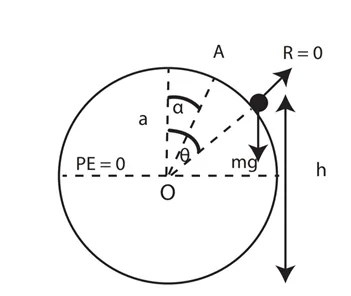
- අංශුව ඉවත්ව යන ලක්ෂ්යයට මේසයේ සිට ඇති දුර = h නම්,
h = a + a cos θ
h = a + a × ⅔ cos α ; (2) ප්රකාශයෙන්,
h = a (1 + ⅔ cos α)
02. සුමට කුහර ගෝලයක් ඇතුළත අංශුවක වෘත්ත චලිතය.
- මෙහිදීද ඉහත (01) හි ගැටලු ආකාරයට අනුවම ගැටලු විසඳීම සිදු වේ. උදාහරණයක් ලෙස පහත ගැටලු ඇසුරින් එය පැහැදිලි කරමු.
උදා: අරය a හා කේන්ද්රය O ද එහි පහළම ලක්ෂ්යයේ ඇති m ස්කන්ධය සහිත අංශුවක් යටි අත් සිරස සමඟ θ කෝණයක් සාදන විට එහි ස්පර්ශීය ප්රවේගය හා ඒ මත එම අවස්ථාවේදී අභිලම්භ ප්රතික්රියාව සොයන ආකාරය පිළිබඳ සාකච්ඡා කරමු.
- මෙම ගැටලු ආකාරයේදී ද A අවස්ථාව හා B යන සාධාරණ අවස්ථාව සළකා ශක්ති සංස්ථිති නියමය යොදා සාධාරණ අවස්ථාවේදී අංශුවේ ස්පර්ශීය ප්රවේගය ලබා ගනියි.
- එම අවස්ථාවේදී අභිලම්භ ප්රතික්රියාවේ විශාලත්වය ලබා ගැනීමට කේන්ද්රය දෙසට F = ma යොදා ගනියි. මෙහිදී ද ත්වරණය සඳහා පෙර ආකාරයටම ස්පර්ශීය ප්රවේගය යෙදෙන ප්රකාශනය යොදා ගනියි. (a = v2/r)
03. ලුහු අවිතන්ය තන්තුවක් මගින් අචල ලක්ෂ්යයකට සම්බන්ධ කර ඇති අංශුවක සිරස් වෘත්ත චලිතය.
- අංශුවක් සිරස් වෘත්තයක චලනය වන විට සෑම විටම ගමන් කරන දිශාවට බරෙහි සංරචකයක් ක්රියා කරන බැවින් ස්පර්ශ ත්වරණයක් පවති.එමනිසා ප්රවේගය සෑම මොහොතකම වෙනස් වෙමින් පවතී.මෙහිදී සිරස් බල සමතුලිත කල නොහැකි බැවින් ගැටලු විසදීමට ශක්ති සංස්තිති නියමය භාවිතා කරයි.
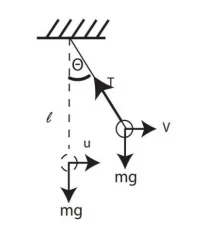
-mgl + ½mu² = -mgl cos θ + ½mv²
v² = u² – 2gl + 2gl cos θ ———-(1)
කේන්ද්රය දෙසට,
F = ma
T – mg cos θ = ma
a = v²/l වේ.
T – mg cos θ = \frac{mv^2}l
T – mg cos θ = \frac ml(u² – 2gl + 2gl cos θ)
(1) න් ආදේශය,
T = \frac ml(u² – 2gl + 3gl cos θ)———(2)
V = 0 වන විට, θ = θ₁ ලෙස ගනිමු.
(1) න් ,
v² = u² – 2gl + 2gl cos θ
0 = u² – 2gl + 2gl cos θ₁
cos θ₁ = \frac{2gl-u^2}{2gl}
T = 0 වන විට, θ = θ₂ ලෙස ගනිමු
(2) න්,
T = \frac ml (u² – 2gl + 3gl cos θ)
0 = \frac ml(u² – 2gl + 3gl cos θ₂)
cos θ₂ = \frac{2gl-u^2}{3gl}
01 අවස්ථාව ; u² < 2gl විට,
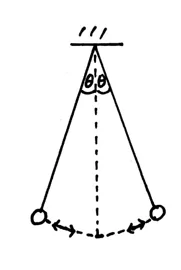
- මෙවිට, cosθ₁ > 0 ද, cos θ₂ > 0 ද වේ.
- cosθ₁ > cos 90˚, cos θ₂> cos 90˚
- 0<θ₁< 90˚, 0<θ₂<90˚
- θ₁ හා θ₂ යන දෙකම සුළු කෝණ වේ.
- cos θ₁ > cos θ₂
- එනම් θ₁ < θ₂
- මෙහිදී පලමුව අංශුවේ ප්රවේගය 0 වීම සිදු වේ.
- මෙහිදී අංශුව සරල අවලම්භනයක චලිතයක් ඇති කරයි.
ඉදිරියේදී ප්රශ්න ඇතුලත් වන්නේ මෙතනටයි.

