03.08.04 – සිරස් වෘත්ත චලිතය හා සම්බන්ධ ගැටලු විසඳීම-2

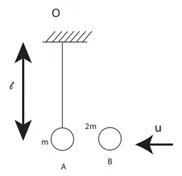
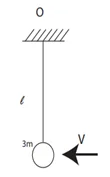
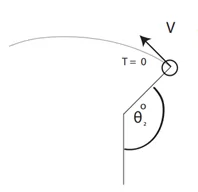
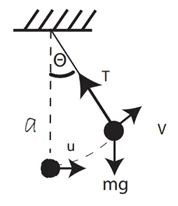
උදා:     ස්කන්ධය m kg වන A අංශුවක් l m වන අවිතන්‍ය තන්තුවකින් අචල O ලක්ෂයකට එල්ලා ඇත. u ප්‍රවේගයෙන් තිරස්ව චලිතවන ස්කන්ධය 2m kg වන B අංශුවක් A හි වැදී හාවේ.සං‍යුක්ත අංශුව ක්ෂණිකව නිසල වන විට තන්තුව සිරසට 60˚ කින් ආනත වේ. u=\frac{3\sqrt{gl}}2බව පෙන්වන්න. θ = 60 විට තන්තුවේ ආතතිය \frac{3mg}2  බව පෙන්වන්න.

ගම්‍යතා සංස්ථිති නියමයෙන්

m×0 + 2m×u = 3m×v

                      v =\frac{2u}3                     (1)

ශක්ති සංස්ථිති නියමයෙන්,

-3mgl + ½×3mv² = -3mgl cos 60 + ½×3mg×v₁²

මෙහි v₁ = 0 වේ.(අංශුව ක්ෂණිකව නිශ්චල වන බව දී ඇති බැවින්)

-3mgl + ½×3mv² = -3mgl cos 60˚

-3mgl + ½×3mv² = -3mgl×½

                          v² = gl

(1) න් ආදේශය,

(\frac{2u}g)² = gl

     u² = \frac{9gl}4

       u = \frac{3\sqrt{gl}}2

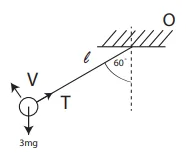
අංශුවට කේන්ද්‍රය දෙසට

                             F = ma 

T – 3mg cos 60˚ = 3mv₁²/l

v₁ = 0 බැවින්,

T = \frac{3mg}2

02 අවස්ථාව ; u² = 2gl විට,

• මෙවිට ,cos θ₁ = 0  ද,  cos θ₂ = 0 ද වේ.
• cos θ₁ =  cos 90˚, cos θ₂ = cos 90˚
• θ₁ = 90˚, θ₂ =90˚   ද වේ.
• මෙහිදී තන්තුව තිරස්වන විට ප්‍රවේගය හා ආතතිය යන 2 ම 0 වීම සිදු වේ.

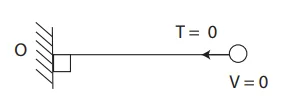
03 අවස්ථාව ; 2gl< u² < 5gl විට,

• මෙවිට ,cos θ₁< 0  ද,  cos θ₂< 0 ද වේ.
• cos θ₁< cos 90, cos θ₂ < cos 90˚
• θ₁> 90˚, θ₂>90˚
• මෙහිදී θ₁ හා θ₂ යන දෙකම මහා කෝණ වේ.
• cos θ₁< cos θ₂
• θ₁ > θ₂
• මෙහිදී පලමුව ආතතිය ශූන්‍ය වීම සිදු වේ.
• ප්‍රවේගය ශූන්‍ය වීමක් සිදු නොවන බැවින් මෙවිට අංශුව ප්‍රක්ෂිප්තයක් ආකාරයෙන් ගමන් කරයි.

උදා:     දිග l වූ තන්තුවකින් ද ලක්ෂ්‍යයක එල්ලා ඇති බර අංශුවක් පහළම තැන සිට  u ප්‍රවේගයෙන් ප්‍රක්ෂේපණය කල විට 120˚ කෝණයකට පසු තන්තුව බුරුල් වේ නම් u²= \frac{7gl}2 බව පෙන්වන්න.

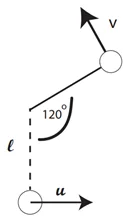
ශක්ති සංස්තිති නියමයෙන්,

-mgl + ½mu² = mgl cos 60 + ½mv²

                     v² = u² – 2gl – 2gl cos 60

                     v² = u² – 2gl (1 + ½)

                     v² = u² – 3gl 

කේන්ද්‍රය දෙසට 

                          F = ma 

T + mg cos 60˚ = 3mv²/l

                            T = – mg cos 60˚ +  \frac ml (u² – 2gl – 2gl cos 60˚)

තන්තුව බුරුල්වන බැවින් T = 0 වේ.

                            0 = u² – 2gl -3lg cos 60˚

                         u² = 2gl + \frac{3gl}2

                         u² = \frac{7gl}2

04 අවස්ථාව ; u² = 5gl විට,

cos θ₁ = \frac{2gl-u^2}{2gl}

cos θ₁ = \frac{2gl-5gl}{2gl}

cos θ₁ = \frac{-3gl}{2gl}

cos θ₁ = \frac{-3}2

• මෙය විය නොහැක. (-1 < cos θ < 1 අතර බැවින්)
• එමනිසා මෙහිදී ප්‍රවේගය 0 වීම සිදු නොවේ.

cos θ₂ = \frac{2gl-u^2}{3gl}

cos θ₂ = \frac{2gl-5gl}{3gl}

cos θ₂ = -1

cos θ₂ = Cos 180˚

       θ₂ = 180˚

• මෙහිදී ඉහළම ලක්ෂ්‍යයේදී ආතතිය 0 වීම සිදු වේ.
• නමුත් මෙහිදී වෘත්ත චලිතය සම්පූර්ණ වීම සිදු වේ.

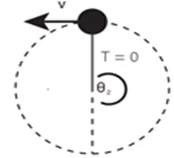
05 අවස්ථාව ; u² > 5gl විට,

• මෙවිට , cosθ₁< -1 ද,  cos θ₂< -1 ද වේ.
• මෙම අවස්ථා 2 දී ම පවතින අගයන් සිදු විය නොහැකි බැවින් මෙවිට ප්‍රවේගය හෝ ආතතිය 0 වීමක් සිදු නොවේ. අංශුව පහසුවෙන් වෘත්ත චලිතය සම්පූර්ණ කරයි.

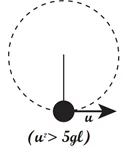
උදා:     දිග a වූ අවිතන්‍ය තන්තුවකින් අචල ලක්ෂ්‍යයක සිට එල්ලන ලද අංශුවකට එහි පහත්ම පිහිටීමේ තිබෙන විට තිරස් u ප්‍රවේගයක් ලබා දෙයි.

1. අංශුව පරිභමණ ඇති කිරීමට නම් u² ≥ 5gl විය යුතු බව, තන්තුවට අඩුම වශයෙන් අංශුවේ බර මෙන් 6 ගුණයක ආතතියක් දැරිය යුතු බවත් පෙන්වන්න.
2. u² = \frac{7ga}2 නම් අංශුව එහි පහත්ම ලක්ෂයේ මට්ටමෙන් \frac{3a}2 උසකදී වෘත්තාකාර පෙත හැර යන බවත් පෙන්වන්න.

ශක්ති සංස්ථිති නියමයෙන්,

-mgh + ½mu² = mgh cos θ + ½mv²

                      v² = u² – 2ga + 2ga cos θ               (2) 

කේන්ද්‍රය දෙසට 

                      F = ma

T – mg cos θ = \frac{mv^2}a

 T – mg cosθ = \frac ma( u² – 2ga + 2ga cos )

                        T = \frac ma(u² – 2ga + 3ga cos θ)

(i) අංශුව පරිභ්‍රමණය වීමට නම් θ = 180 ද, T ≥ 0 ද විය යුතුය.

T =  \frac ma(u² – 2ga + 3ga cos θ) බැවින්,

\frac ma(u² – 2ga + 3ga cos 180˚) ≥ 0 වේ.

         u² – 2ga + 3ga cos 180˚≥ 0

                                                  u² ≥ 2ga – 3ga cos 180˚

                                                  u² ≥ 2ga – 3ga cos(-1)

                                                  u² ≥ 5ga වේ.

උපරිම ආතතිය පවතින්නේ පහලම ලක්ෂ්‍යයේ බැවින්,

T_{උපරිම} = \frac ma(u² – 2ga + 3ga cos θ ) cos θ = 0 විය යුතුය.

T_{උපරිම} = \frac ma(u² – 2ga + 3ga × 1)

T_{උපරිම} = \frac ma(5ga – 2ga + 3ga)   ;   (u² = 5ga නිසා)

T_{උපරිම} = \frac ma × 6 ga

T_{උපරිම} = 6mg වේ.

(ii) අංශුව වෘත්ත චලිතයෙන් මිදීමට නම් T = 0 විය යුතුය.

එවිට u² =\frac{7ga}2 බැවින්

           T = \frac ma(u² – 2ga + 3ga cos θ)

                   T= \frac ma(7ga2- 2ga + 3ga cos θ)

           0 = \frac ma(7ga – 4ga + 6ga cos θ)

6 cos θ = -3

   cos θ = – ½

  cos θ = 120˚

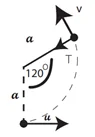
v² = u² – 2ga + 2ga cos θ

v² = u² – 2ga + 2ga cos 120

v² = u² – 2ga + 2ga×-½

v² = \frac{7ga}2 – 2ga -ga

v² = \frac{ga}2

 v = (\frac{ga}2)½

• මෙහි  v = (\frac{ga}2)½ වන බැවින් අංශුව වෘත්තාකාර පෙත හැර යයි.

04. සිරස් නළයක් තුළ අංශුවක චලිතය.

(2006 A/L)

උදා: පහත රූපයේ දැක්වෙන්නේ කේන්ද්‍රය O, අරය a හා කෝණය 2(π – α) වු වෘත්ත චාපයක ආකාරයට නමන ලද ABC සුමට සිහින් නළයකි. මෙහි α සුළු කෝණයක් වෙයි. A, C විවෘත දෙකෙළවර එකම තිරස් මට්ටමේ තිබෙන පරිදි නළය තිරස් තලයක සවි කරයි. නළයේ පහත්ම ලක්ෂ්‍යයේ (B) අංශුවක් තබා, නළය දිගේ තිරස් u ප්‍රවේගයකින් ප්‍රක්ෂේපණය කරයි. නළය දිගේ A කෙළවරට පැමිණ අනතුරුව නිදහසේ ගුරුත්වය යටතේ ප්‍රක්ෂිප්තයක් ලෙස චලනය වී, C කෙළවරින් නැවත නළයට ඇතුල් වෙයි. අංශුව A හිදී නළයෙන් ඉවත් වන විට එහි ප්‍රවේගය සොයා u² = ga [2 (1 + cos α) + sec α] බව පෙන්වන්න. තවද අංශුව ළගා වන උපරිම උස O ට ඉහළින් \frac a2(cos α + sec α) බවත් පෙන්වන්න.

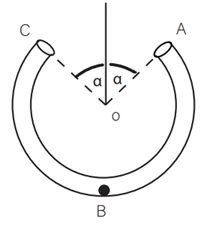
ශක්ති සංස්ථිති නියමයෙන්,

B හි ශක්තිය = C හි ශක්තිය

mg × 0 + ½ mu² = mg (a – a cos θ) + ½ mv²

                           u² = 2g (a – a cos θ) + v²

                           v² = u² – 2ga (1 – cos θ)                 (1)

• ගැටලුවේ දී අභිලම්භ ප්‍රතික්‍රියාව සඳහා ප්‍රකාශනයක් අසා නොමැති උවද, C හිදී අංශුව මත අභිලම්භ ප්‍රතික්‍රියාව සොයන ආකාරය අප පහත පරිදි සිදු කරමු.

C හිදී,

                       F = ma

R – mg cos θ = mv²/r

R – mg cos θ = m [u² – 2ga (1 – cos θ)]/ a   ;   (1) න්,

                      R = mg cos θ + (mu²/a) – 2mg (1 – cos θ)

                      R = 3mg cos θ – 2mg + (mu²/a) 

                      R = mg (3 cos θ – 2) + (mu²/a) 

• නැවත ගැටලුව විසඳමු.

θ = (π – α) විට (1) න්,

v₁² = u² – 2ga [1 – cos (π – α)]

v₁² = u² – 2ga [1 – (-cos α)]

v₁² = u² – 2ga (1 + cos α)                  (2)

AD චලිතයට,

↑ S = ut + ½ at²

   0 = v₁ sin α t – ½ gt²

   0 = v₁ sin α – ½ gt

    t = \frac{2v_1\sin\alpha}g

AD චලිතයට,

      ← S = ut

  2a sin α = v₁ cos α × (\frac{2v_1\sin\alpha}g)

                a = v₁ cos α × (v₁/g)

              ag = v₁² cos α

 ag/cos α = v₁²

ag/cos α = u² – 2ga (1 + cos α)   ;   (2) න්,

              u² = ga [2 (1 + cosα) + sec α]                (3)

A සිට උපරිම උස තෙක් චලිතයට,

↑ v² = u² + 2as

    0 = (v₁ sin α)² – 2gs   ;   s යන්න රූපයේ ලකුණු කොට ඇත.

    0 = v₁² sin² α – 2gs

2gs = v₁² sin² α 

2gs = [u² – 2ga (1 + cos α)] sin² α

2gs = {ga [2 (1 + cosα) + sec α] – 2ga (1 + cos α)} sin² α   ;   (3) න් u² සඳහා   

2gs = [2ga (1 + cos α) + ga sec α – 2ga (1 + cos α)] sin² α

   2s = a sec α sin² α

     s = \frac a2 sec α sin² α

∴ O සිට ඉහළ නගින උපරිම උස = s + a cos α

                                                           =  \frac a2 sec α sin² α + a cos α

                                                    = \frac a2(2 cosα + sec α sin² α)

                                                            = \frac a2 (cosα + cos α + sec α sin² α)

                                                            =  \frac a2(cosα + sec α cos² α + sec α sin² α)

                                                            =  \frac a2[cosα + sec α (cos² α + sin² α)]

                                                            =  \frac a2(cosα + sec α × 1)

                                                            =  \frac a2(cos α + sec α)

(2019 A/L)

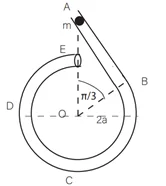
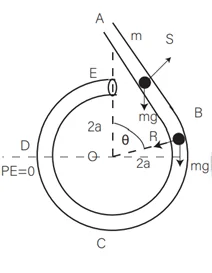
උදා: රූපයේ පෙන්වා ඇති පරිදි සුමට සිහින් ABCDE බටයක් සිරස් තලයක සවි කර ඇත. දිග 2\sqrt3 a වූ AB කොටස ඍජු වන අතර එය B හි දී අරය 2a වූ BCDE වෘත්තාකාර කොටසට ස්පර්ශක වේ. A හා E අන්ත O කේන්ද්‍රයට සිරස්ව ඉහළින් පිහිටයි. ස්කන්ධය m වූ P අංශුවක් A හි දී බටය තුළ තබා නිශ්චලතාවයේ සිට සීරුවෙන් මුදා හරිනු ලැබේ. OA සමඟ θ (π/3 < θ < 2π) කෝණයක් OP සාදන විට P අංශුවේ වේගය, v යන්න, v² = 4ga (2 – cos θ) මගින් දෙනු ලබන බව පෙන්වා, එම මොහොතේ දී P අංශුව මත බටයෙන් ඇති කරන ප්‍රතික්‍රියාව සොයන්න. 

P අංශුව A සිට B දක්වා චලිතයේ දී එය මත බටයෙන් ඇති කරන ප්‍රතික්‍රියාව ද සොයන්න. 

P අංශුව B පසු කරන විට P අංශුව මත බටයෙන් ඇති කරන ප්‍රතික්‍රියාව ක්ෂණිකව වෙනස් වන බව පෙන්වන්න.

• ලිවිය යුතු අවසාන පිළිතුර සඳහා, මෙහි දක්වා ඇති පරිදි ලකුණු බෙදී යාම සිදු වේ.

P අංශුවට ශක්ති සංස්ථිති මූලධර්මය යෙදීමෙන්,

½ mv² + mg (2a cos θ) = 0 + mg × 4a

                                         v² = 4ga (2 – cos θ)   ;   (π/3 < θ < 2π)

නළය තුලට වෘත්ත චලිතය සඳහා,

                       F = ma               

mg cos θ + R = \frac{mv^2}{2a}

                       R = \frac m{2a}  [4ga (2 – cos θ)] – mg cos θ                              +

                       R = mg (4 – 3 cos θ) > 0                   (1)

∴ මෙම ප්‍රතික්‍රියාව O කේන්ද්‍රය වෙතට වේ.

ඍජු නළය ඇතුළට චලිතය සඳහා,

                            F = ma 

S – mg cos (π/3) = m(0)

                              S =  \frac{mg}2

B වෙත ළඟා වීමට මොහොතකට පෙර ප්‍රතික්‍රියාව = \frac{mg}2

                  B පසු කර මොහොතකට පසු ප්‍රතික්‍රියාව = \frac52mg

ඒ අනුව, B හි දී ප්‍රතික්‍රියාව විශාලත්වයෙන් \frac{mg}2 සිට \frac52 mg දක්වා වෙනස් වන අතර දිශාව පිටත සිට ඇතුළතට වෙනස් වේ.

• පසුගිය විභාග ප්‍රශ්න පත්‍රයන්හි 2011(නව), 2012(පැරණි) හා 2017 යන ගැටලු විසදීමෙන් මෙම පාඩමෙහි අඩංගු සිද්ධාන්තයන් පිළිබදව  අවබෝධයක් ලබා ගත හැකිය.

ඉදිරියේදී ප්‍රශ්න ඇතුලත් වන්නේ මෙතනටයි.