සංයුක්ත ගණිතය II (ව්යවහාර ගණිතය)ප්රශ්න පත්රයේ B කොටසේ(රචනා ප්රශ්න)12 වැනි ප්රශ්නයේ මෙම පාඩමේ අඩංගු සිද්ධාන්ත අඩංගු වේ.
සාපේක්ෂ ත්වරණය
උදා:
1) ස්කන්ධය M වූ කුඤ්ඤයක් එහි එක් මුහුණතක් සුමට තිරස් මේසයක් සමග ස්පර්ශව සමතුලිතව තබා ඇත.එහි තිරසට α කෝණයකින් ආනත මුහුණතක් මත ස්කන්ධය m වූ අංශුවක් තබා පද්ධතිය මුදා හරිනු ලැබේ.අංශුව කුඤ්ඤයේ ගුරුත්ව කේන්ද්රය හරහා යන වැඩිතම බෑවුම් රේඛාව ඔස්සේ චලිත වන්නේ යැයි උපකල්පනය කරමින් ,
- කුඤ්ඤයේ ත්වරණය
- කුඤ්ඤයට සාපේක්ෂව අංශුවේ ත්වරණය
- කුඤ්ඤය හා අංශුව අතර අභිලම්බ ප්රතික්රියාව සොයන්න.
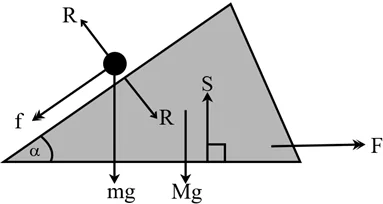
a(කූ.පො.)→F
a(අං.කූ.) = ![]()
a(අං.පො.) = a(අං.කූ.) + a(කූ.පො.)
= f-F\cos\alpha
අංශුවට ![]() F = ma යොදමු.
F = ma යොදමු.
mgsinα = m(f – Fcosα)
gsinα +Fcosα = f —–> \boldsymbol①
පද්ධතියටම → F =ma යොදමු.
0 = MF + m( F – fcosα )
mfcosα= ( m + M )F
f = (( m + M ) F)/mcosα —–>\boldsymbol②
\begin{array}{l}gs\mathrm{in}\alpha\;+\;F\cos\alpha\;=\dfrac{(m+M)F}{m\cos\alpha}\\g\sin\alpha\;=\;\dfrac{(m+M)F}{m\cos\alpha}\;-\;F\cos\alpha\\g\sin\alpha\;=\;\dfrac{(m+M-m\cos^2\alpha)F}{m\cos\alpha}\;\;\\mg\sin\alpha\cos\alpha\;=\;(m\sin^2\alpha\;+M)F\end{array}F = \dfrac{mg\sin\alpha\cos\alpha}{(m\sin^2\alpha+M)} //
\boldsymbol② ට ,
f = \frac{(m+M)g\sin\alpha}{(m\sin^2\alpha+M)} //
කුඤ්ඤයට → F=ma
Rsinα = MF
R = \frac M{\sin\;\alpha}\;\times\frac{mg\sin\alpha\cos\alpha}{M+m\sin^2\alpha}
= \frac{\displaystyle mMg\cos\alpha}{(M+m\sin^2\alpha)}//
2) ස්කන්ධය M වූ කුඤ්ඤයක් සුමට තිරස් තලයක් මේසයක් මත තබා එහි තිරසට α ආනත මුහුණත මත ස්කන්ධය m වූ අංශුවක් තබා එම අංශුව අඩංගු මුහුණත ඉදිරියට ඇතිව කුඤ්ඤය චලනය වන පරිදි කුඤ්ඤය මත මේසයට සමාන්තරව P බලයක් යොදනු ලැබේ. කුඤ්ඤයේ ත්වරණය සොයන්න.
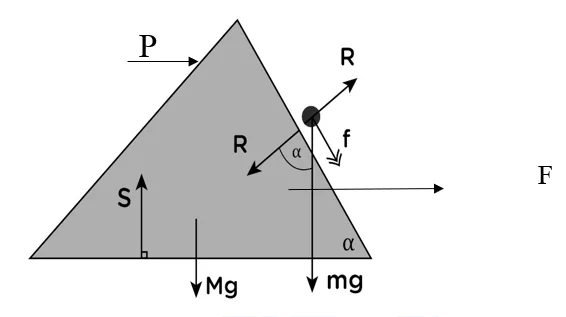
a(කූ.පො)= → F
a(අං.පො) = f
අංශුවට F = ma යෙදීමෙන්
mgsinα = m( f +Fcosα )
gsinα – f = Fcosα—–>\boldsymbol①
පද්ධතියට → F=ma
P = m(fcos α + F)+MF
(\frac{\displaystyle P}{(m+M)}\;\;-\;F\;)\frac{\displaystyle1}{\cos\alpha\;\;} = f —–>\boldsymbol②
\boldsymbol② න් \boldsymbol① ට
\begin{array}{l}gs\mathrm{in}\alpha\;-\;\frac{(P-F(m+M))}{m\cos\alpha}\;=\;F\cos\alpha\\g\sin\alpha\cos\alpha\;-\;(\frac{P-F(m+M)}m)\;=\;F\cos^2\alpha\\mg\sin\alpha\cos\alpha\;-P+F(m+M)-mFc\mathrm{os}^2\alpha=0\;\;\\mg\sin\alpha\cos\alpha\;-P+mF\sin^2\alpha+MF\;=\;0\end{array} \begin{array}{l}F(m\sin^2\alpha+M)\;=\;P\;-\;m\sin\alpha\cos\alpha\\F\;=\;\dfrac{P-mg\sin\alpha\cos\alpha}{(m\sin^2\alpha+M)}\end{array}3) තිරසට α ආනත සුමට තලයක් මත ස්කන්ධය M වූ කුඤ්ඤයක එක මුහුණතක් ආනත තලය සමග ස්පර්ශ වන පරිදි තබා කුඤ්ඤයේ තිරස් මුහුණත මත ස්කන්ධය m වූ අංශුවක් තබා පද්ධතිය නිසලතාවයෙන් මුදා හරිනු ලැබේ. කුඤ්ඤයේ ත්වරණය හා අංශුවේ ත්වරණය සොයන්න.
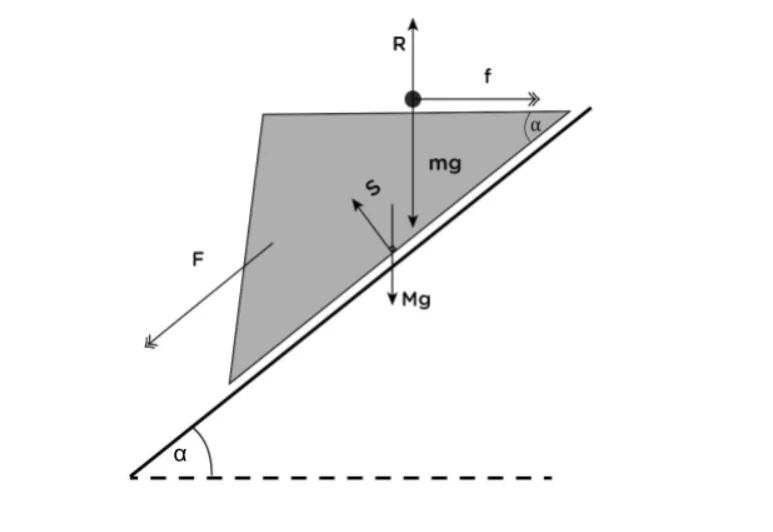
a(කූ.පො). =F
a(අං.පො.) = →f
a(අං.පො.) = a(අං.කූ.) + a(කූ.පො.)
= → f +F
→ F = ma අංශුවට
0 = f – Fcosα
Fcosα=f —–>\boldsymbol①
පද්ධතියටම F=ma
Mgsinα + mgsinα = MF + mf –mfcosα —–>\boldsymbol②
\boldsymbol①න් \boldsymbol②ට
Mgsinα +mgsinα = MF + mf – mfcos2α
F=\dfrac{(m+M)g\sin\alpha}{(M+m\sin^2\alpha)}කුඤ්ඤයේ ත්වරණය = \dfrac{(m+M)g\sin\alpha}{(M+m\sin^2\alpha)}
\boldsymbol①න්,
f=\dfrac{(M+m)g\sin\alpha}{(M+m\sin^2\alpha)}\cos\alphaඅංශුවේ ත්වරණය = \dfrac{(M+m)g\sin\alpha}{(M+m\sin^2\alpha)}\cos\alpha
4) සුමට තිරස් මේසයක් මත ස්කන්ධය M වූ කුඤ්ඤයක් තබා එහි තිරසට α ආනත මුහුණතේ ස්කන්ධය m වූ අංශුවක් පහලම දාරය මත තබා මුහුණත දිගේ ඉහලට u ප්රවේගයෙන් ප්රක්ෂේපනය කරනු ලැබේ.(වැඩිතම බෑවුම දිගේ)අංශුව නැවත ආරම්භක ලක්ෂ්යයට පැමිණීමට ගත වන කාලය සොයන්න.
a කූ.පො.= →F
a අං.කු. = f
a අං.පො.= a අං.කූ. + a කූ.පො.
= f + →F
අංශුවට F=ma
-mgsinα=m(f+Fcosα)
-gsinα-Fcosα=f
F=\frac{-g\sin\alpha-f}{\cos\alpha\;} \xrightarrow{}\boldsymbol①
පද්ධතියටම F=ma
0=m(F+fcosα) + MF
0=F(M+m)+fcosα
f= \frac{-F(M+m)}{\cos\alpha} F=\frac{-mf\cos\alpha}{(m+M)}\xrightarrow{}\boldsymbol②
\boldsymbol②න් \boldsymbol①ට
\frac{-(g\sin\alpha+f)}{\cos\alpha}\;=\;\frac{(-f\cos\alpha)}{(m+M)}(m+M)gsinα + (m+M)f = fcos^2\alpha
f(cos^2\alpha – m – M)= (m+M)gsinα
f=-\{\frac{(m+M)g\sin\alpha}{m\sin^2\alpha+M}\} //
කාලය T නම්,
කුඤ්ඤයට සාපේක්ෂව අංශුවේ චලිතයට,
\begin{array}{l}s=ut+\dfrac12at^2\\0=uT+\dfrac12fT^2\\T=-(\dfrac{2u}f)\\T=(\dfrac{2u(m\sin\alpha+M)}{(m+M)g\sin\alpha})\end{array}5) ස්කන්ධය M වූ සුමට කුඤ්ඤයක් ආරෝහකයක සුමට තිරස් බිමක් මත තබා අංශුවක් කුඤ්ඤයේ පහලම දාරයෙන් ආරම්භ කර u ප්රවේගයෙන් මුහුණත දිගේ ප්රක්ෂේපනය කරනු ලැබේ.අරෝහකය ඉහල නගින ත්වරණය a වේ.අංශුව තබා ඇති කුඤ්ඤයේ මුහුණතේ ආනතිය තිරසට α වන අතර කුඤ්ඤයේ උස h වේ.අංශුව නැවත ප්රක්ෂේපන ලක්ෂයට නොපැමිනිමට අවශ්යතාවය ලබා ගන්න.අංශුවේ ස්කන්ධය KM ලෙස ගන්න.
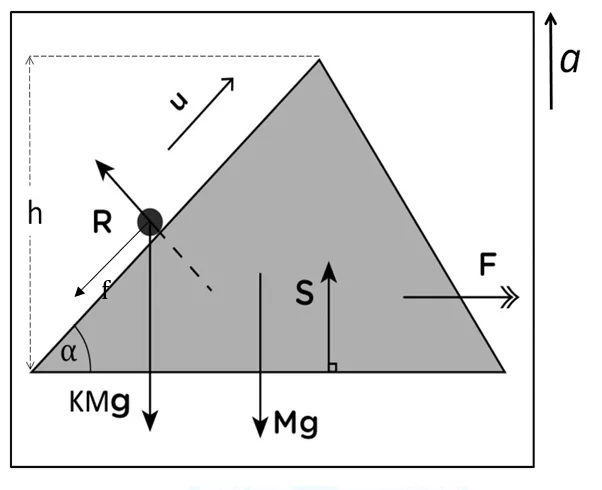
ආ.පො. = ↑a
අං.කූ. = ![]() f
f
කූ.ආ. = →F
a කූ.පො. =a කූ.ආ. +a ආ.පො.
= →F +↑a
a අං.පො. =a අං.කූ. +a කූ.පො.
= f + →F + ↑a
අංශුවට F = ma
KMgsinα = KM( -Fcosα + f – asinα )
gsinα= f – Fcosα – asinα
F =\frac{(f\;–\;a\sin\alpha\;-\;g\sin\alpha\;)}{\cos\alpha}\xrightarrow{}\boldsymbol①
පද්ධතියටම →F=ma
0 = MF + KMF – KMfcosα
F =\frac{Kf\cos\alpha}{(\;1+k\;)}[/latex]\xrightarrow{}\boldsymbol②
\boldsymbol① හා \boldsymbol②න්
\frac{(f-a\sin\alpha-g\sin\alpha}{\cos\alpha\;})=\;\frac{Kf\cos\alpha}{(\;1+K\;)}(1+K)(g+a)sinα = f(1+Ksin^2\alpha)
f =\frac{(1+K)(g+a)\sin\alpha}{(1+Ksin^2\alpha)} //
v^2=u^2+2\lbrack\frac{(1+K)(a+g)\sin\alpha}{(1+ksin^2\alpha)}\rbrack\frac h{sin\alpha}අංශුව නැවත නොපැමිනිමට නම්, v >0 විය යුතුය.
එනම් v^2 > 0 විය යුතුය.
u^2+\frac{2(1+K)(a+g)h}{(1+Ksin^2\alpha)} > 0
u >\surd\frac{(2(1+K)(a+g)}{(1+Ksin^2\alpha)} විය යුතුය.
6) කේන්ද්රික හරස්කඩ ABC ත්රිකෝණයක් වන M ස්කන්ධය ඇති සුමට කුඤ්ඤයක් AB මුහුණත සුමට තිරස් මේසයක් ස්පර්ශ කරමින් නිසලව පවති. BAC = α , ABC තලයෙහි ABට සමාන්තරව කුඩා විශ්කම්භයක් ඇති සුමට සිදුරක් විදිනු ලැබේ.ස්කන්ධය m වන අංශුවක් එම සිදුරෙහි තබා එය C ශිර්ෂය වටා ඇද තිබෙන අවිතන්ය තන්තුවකින් AC පාදය මත තිබෙන ස්කන්ධය m’ වන අංශුවකට සම්බන්ධ කර මුළු පද්ධතියම නිසලතාවයේ සිට මුදාහරිනු ලැබේ.m’cosα >m නම් කුඤ්ඤය BA දිශාව ඔස්සේ චලිත වන බව පෙන්වන්න.
mහි ත්වරණය \frac{m'g\sin\alpha(m+m'+M)}{(m+m')(m+m'+M)-(m'\cos\alpha-m)^2} බව පෙන්වන්න.
කුඤ්ඤය = M
a(m,M) = →f
a(M,E)= ←F
a(m’,M)=
a(m,E)= a(m,M) + a(M,E)
= →f + ←F
= ←(F-f)
a(m’,E) = a(m‘,M) + a(M,E)
= f + ←F
= f + Fcosα + ←F+fcosα
mට →F=ma යොදමු.
T = m(f-F) \xrightarrow{}\boldsymbol①
m’ට F=ma යොදමු.
m’gsinα-T= m'(f+Fcosα) \xrightarrow{}\boldsymbol②
\boldsymbol①+\boldsymbol②
m’gsinα = m(f-F) + m'(f+Fcosα)
m’gsinα = (m+m’)f + (m’cosα – m )F\xrightarrow{}\boldsymbol③
පද්ධතියට ← F=ma
0 = MF + m(F – f) +m’ (F +fcosα)
0 = (M+m+m’ )F + (m’ cosα – m)f \xrightarrow{}\boldsymbol④
\boldsymbol③×( m’cosα – m ) –\boldsymbol④×(m+m’ )
m’gsinα( m’cosα – m )= (m^/cos\alpha-m)^2 F – (m+m’ )(M+m+m’ )F
F =\frac{(m^/g\sin\alpha(m^/\cos\alpha-m))}{(m^/cos\alpha-m)^2-(m+m^/)(M+m+m')}
F ලකුණු කර ඇති දිශාවට පවතී නම්,F > 0 විය යුතුය.
m,M,m’ ස්කන්ධ නිසා (m+M+m’ )>0
F > 0
m’gsinα( m’cosα-m)>0
m’cosα > m
1×(M+m+m’ ) – 2 ×( m’cosα-m)
m’gsinα(M+m+m’ ) = (m+m’ )(m’ cosα-m)f – (m^/cos\alpha-m)^2f
f = \frac{(m^/g\sin\alpha(M+m+m^/)}{(m+m^/)(m^/cos\alpha-m)-(m^/cos\alpha-m)^2)} //
7) α ආනතියෙන් යුත් සුමට කුඤ්ඤයක් සුමට තිරස් මේසයක් මත තබා ඇත.දෙකෙළවර m,m’ ( m>m’ ) ස්කන්ධ ඈදු 2l දිග ලුහු අවිතන්ය තන්තුවක් කුඤ්ඤයේ ඉහල ආනත මුහුනතින් නෙරා තිබෙන p සුමට කප්පියක් වටා දමා ඇත.අංශු කුඤ්ඤයේ මුහුණත සමග ස්පර්ශව ඇත.ආරම්භයේදී අංශු එකිනෙක ආසන්නවද , සුමට කප්පියේ සිට l දුරින් පිහිටන පරිදිද තබා ඇත.තන්තුවේ එක් එක් කොටස නුබුරුල්ව ආනත මුහුණතේ උපරිම බෑවුම් රේඛාවකද පිහිටා ඇත.බරින් අඩු අංශුව p වෙත ඒමට පෙර කුඤ්ඤයේ ත්වරණය \frac{(m-m')^2g\sin\alpha\cos\alpha}{M(m+m')+(m+m')^2\sin^2\alpha+4mm'} බව පෙන්වන්න.කුඤ්ඤයේ ස්කන්ධය M වේ.
a(m’,M)=f a(m,M) = f a(M,E) =→F
a(m’,E)= a(m’+M) + a(M,E)
= f + →F
= fsin α + F +fcos α
m,E = m,M + M,E
= f +→F
= fsin α + F – fcos α
mට F=ma යොදමු
mgsinα – T = m(f-Fcosα) \xrightarrow{}\boldsymbol①
m’ට F=ma යොදමු
T – m’gsinα = (f+Fcosα) \xrightarrow{}\boldsymbol②
\boldsymbol①+\boldsymbol②
(m -m’)gsinα = (m+m’)f +(m’- m)Fcosα \xrightarrow{}\boldsymbol③
පද්ධතියට →F=ma යොදමු.
0 = MF +m(F – fcosα) + m'(F + Fcosα)
0 = (M+m+m’)F + (m’- m )fcosα \xrightarrow{}\boldsymbol④
\boldsymbol③×( m’- m )cosα – \boldsymbol④×(m+m’)
(m – m’)gsinα.(m’ – m)cosα = (m^/-m)^2cos^2\alphaF – ( m+ P)(M+m+m’)F
(m-m^/)^2 gsinαcosα = [ ( m+m’) (M+m+m’ ) –(m^/-m)^2cos^2\alpha ] F
= [ M(m+m’ ) +(m+m^/)^2-(m-m^/)^2(1-sin^2\alpha)
= [ M(m+m’) + 4mm’ + (m-m^/)^2sin^2\alpha ]F
F = \frac{(m-m^/)^2g\sin\alpha\cos\alpha)}{(M(m+m^/)+4mm^/+(m-m^/)^2sin^2\alpha)} //
8) රුපයේ p අංශුවක් බිත්තියක වූ L අචල ලක්ෂ්යයකට ලුහු අවිතන්ය තන්තුවක් මගින් සම්බන්ධ කර තිබේ .තන්තුව හරස්කඩ ABCD වන කුඤ්ඤයක Dහි පිහිටි අචල සුමට කප්පියක් උඩින් යමින් අංශුව කුඤ්ඤයේ DA ආනතිය මත නිසලව පවතී. කුඤ්ඤයේ මුහුණත් සුමටද කප්පියේ ස්කන්ධය නොගිනිය හැකි තරම්ද වේ.අංශුව හා කුඤ්ඤය නිසලතාවයෙන් මුදා හැරේ.බිම හා කුඤ්ඤය අතර ප්රතික්රියාව \lbrack\frac{M^2+Mm(3-2\cos\alpha)+m^2(1-\cos\alpha)^2}{M+2m(1-\cos\alpha)}\rbrack බව පෙන්වන්න.p අංශුවේ ස්කන්ධය M ද , කුඤ්ඤයේ ස්කන්ධය M ද වේ.
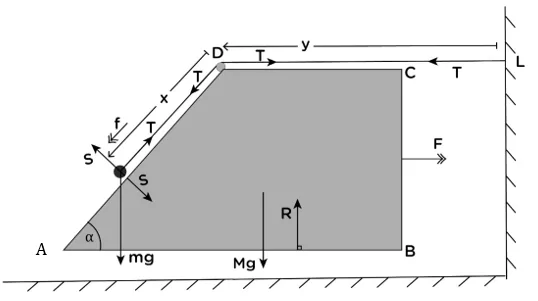
කුඤ්ඤය = w
a(W,E) = →F a( P,W )= 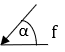
x+y=k(නියතයකි)
අනුයාතව කාලය විෂයෙයේ දෙවරක් අවකලනය කිරීමෙන්,
\ddot x +\ddot y = 0
\ddot x = –\ddot y
f = F
a(P,E) = a(P,W) + a(W,E)
= f + →F
= F(1-cos α) + fsin α
Pඅංශුවට F=ma යොදමු.
mgsinα – T = mf(1 – cosα) \xrightarrow{}\boldsymbol①
පද්ධතියට →F=ma
T= Mf + mf( 1 – cosα) \xrightarrow{}\boldsymbol②
\boldsymbol①+\boldsymbol②
mgsinα = Mf + 2mf( 1 – cosα )
f = \frac{mg\sin\alpha}{(M+2m(1-\cos\alpha\;))\;}
පද්ධතියට ↑F=ma
R – Mg – mg = -mfsinα \xrightarrow{}\boldsymbol③
R –(M+m)g = -m×\frac{mg\sin\alpha}{(M+2m(1-\cos\alpha))} sinα
R = (M+m)g – \frac{(m^2g\sin^2\alpha)}{(M+2m(1-cos\alpha))}
R = [\frac{(M^2+Mm(3-2\cos\alpha)+m^2〖(1-\cos\alpha)〗^2)}{(M+2m(1-cos\alpha))} ]g //
9) ABC හා යනු එකම සුමට තිරස් තලයක සමමිතිකව තබා ඇති එක එකෙහි ස්කන්ධය M වන සුමට සමාන X,Y කුඤ්ඤ දෙකකි.ඒවායේ α කෝණයකින් ආනත මුහුණත් මත එක එකෙහි ස්කන්ධය m වන P,Q අංශු දෙකක් තබා ඇත.රුපයේ පරිදි ඒවා අවිතන්ය තන්තුවකින් සම්බන්ධ කර ඇත.පද්ධතිය නිසලතාවයෙන් මුදාහැරී විට ,
2\surd\frac{((a{M/2m+(1-\cos\alpha)}}{gsin\alpha}) කාලයකදී කුඤ්ඤ දෙක ගැටෙන බව පෙන්වන්න.තන්තුවේ ආතතිය M+\frac{m(1-\cos\alpha)mg\sin\alpha}{(M+2m(1-\cos\alpha))} බව පෙන්වන්න.
a(X,E) = →F
a(P,X) = f
2x + y = k (නියතයකි)
2 \ddot x +\ddot y = 0
2 \ddot x = – \ddot y
2f = 2F
f = F
a(P,E) = a(P,X) + a(X,E)
= f + →F
= F(1-cosα) → F(1-cosα)
Pට F=ma යොදමු.
Mgsinα – T = mF(1-cosα) \xrightarrow{}\boldsymbol①
පද්ධතියට →F=ma
T= MF +MF(1-cosα) \xrightarrow{}\boldsymbol②
\boldsymbol①+\boldsymbol②
mgsinα = MF +2MF(1-cosα)
F = \frac{mg\sin\alpha}{(M+2m(1-\cos\alpha)\;)}
S= \frac12ut^2 (X,Y) යොදමු.
s(X,Y) = 2a
a(X,Y) = a(X,E) + a(E,Y)
= →F + ( – ←F)
= →2F
2a = 1/2 × 2F × t^2
t^2=\frac{2a}Ft^2= 2a ×{\frac{(M+2m(1-\cos\alpha))}{mgsin\alpha} }
= 2a×{\frac{\displaystyle(\frac{\displaystyle2M}{2m}+\frac{\displaystyle2m}m(1-\cos\alpha))}{g\sin\alpha} }
t =2\surd\frac{a{({\displaystyle\frac M{2m}}\;+\;\;\;(1-\cos\alpha)})}{gsin\alpha}
\boldsymbol②න්
T = M +m(1-cosα)F
= M+ m(1-cosα)\frac{mg\sin\alpha}{(M+2m(1-\cos\alpha))} //
Video Links

