සංයුක්ත ගණිතය I (ශුද්ධ ගණිතය) ප්රශ්න පත්රයේ A කොටසේ ගැටලුවක හා B කොටසේ 14 වැනි ගැටලුවෙහි අඩංගු වන්නේ මෙම පාඩමෙහි සිද්ධාන්ත වේ.
සිරස් ස්පර්ශෝන්මුඛ සහිත ප්රස්තාර
උදා: (13.) f (x) = \frac{x^2}{(x-1)(x-5)} ; x ≠ 1 , 5
ඉහත වක්රයේ i) ස්තාවර ලක්ෂ්යය සොයන්න.
ii) f (x) ශ්රිතයේ සාපේක්ෂ උපරිම හා අවම අගයන් සොයන්න.
iii) y = f(x) ශ්රිතයේ සිරස් හා තිරස් ස්පර්ශෝන්මුඛ සොයා වක්රයේ දළ සටහනක් අඳින්න. එනයින්
\frac{x^2}{(x-1)(x-5)\left(℮^{-x}\right)} = 0 හි මූල සංඛ්යාව සොයන්න.
- f(x) = x2/(x2-6x+5)
x විෂයෙන් වරක් අවකලනයෙන්,
\begin{array}{rcl}\;f'(x)\;&=&\frac{2x(x^2-6x+5)-x^2(2x-6)}{(x-1)^2(x-5)^2}\\;f'(x)\;&=&\frac{(2x^3-12x^2+10x-2x^3+6x^2)}{(x-1)^2(x-5)^2}\\;f'(x)\;&=&\frac{(-6x^2+10x)}{(x-1)^2(x-5)^2}\&&\&&\end{array}ස්තාවර ලක්ෂ්යයන් සඳහා,
f’ (x) = 0
\begin{array}{rcl}&&\frac{-x(6x-10)}{(x-1)^2(x-5)^2}\end{array} = 0
x=0 හෝ 6x-10 = 0
x=5/3


x = 0 විට, y = 0 x = 5/3 විට, y = -5/4
(0, 0) අවමයකි. (5/3, -5/4) උපරිමයකි.
Lim x→∞ f(x) = lim x→∞ \begin{array}{rcl}&&\frac{x^2}{(x-1)(x-5)}\&&\end{array}
= lim x→∞ \begin{array}{rcl}&&\frac{x^2}{x^2\left(1-\;{\displaystyle\frac6x}\;+{\displaystyle\frac5{x^2}}\right)}\&&\end{array}
= 1
lim x→±∞ y = 1
තිරස් ස්පර්ශෝන්මුඛ : y = 1
සිරස් ස්පර්ශෝන්මුඛ : x = 1 හෝ x = 5
Lim x→1– y = +∞ lim x→5– y = -∞
lim x→1+ y = -∞ lim x→5+ y =+∞

මෙම ප්රස්තාරයේ ඡේදන ලක්ෂ්ය එකකි.
\frac{x^2}{(x-1)(x-5)}=℮^{-x} විට, සමීකරණයේ මූල ගණන 1 කි.
උදා: (14.) y=\frac{2x^2}{(x^2-4)}
y=\frac{2x^2}{(x^2-4)}y=\frac{2x^2}{(x-2)(x+2)} ; x ≠ 2 , -2
මෙහි x = 2 හා x = -2 වසම තුළ නොමැත. එබැවින් x = 2 හා x = -2 සිරස් ස්පර්ශෝන්මුඛ ලෙස හැඳින්වේ.
\begin{array}{l}\frac{dy}{dx}=\frac{\left(x^2-4\right){\displaystyle\left(2\right)}{\displaystyle\left(2x\right)}{\displaystyle-}{\displaystyle\left(2x^2\right)}{\displaystyle\left(2x\right)}}{\displaystyle\left(x^2-4\right)^2}\\\frac{\displaystyle dy}{\displaystyle dx}=\frac{\left(4x^2-16x-4x^3\right)}{\displaystyle\left(x^2-4\right)^2}\\\frac{\displaystyle dy}{\displaystyle dx}=\frac{-16x}{{\displaystyle\left(x-2\right)^2}{\displaystyle{\displaystyle\left(x+2\right)}^2}}\end{array}ස්තාවර ලක්ෂ්ය සඳහා,
\begin{array}{l}\frac{dy}{dx}=0\\\frac{\displaystyle-16x}{\displaystyle\left(x-2\right)^2\left(x+2\right)^2}=0\;\;\;\;\;\;\;\;\;\;\;x=0\\\end{array}

x = 0 විට, y = 0
lim x→5– y = +∞ lim x→2– y = -∞
lim x→5+ y = -∞ lim x→2+ y = +∞
lim x→∞ y = lim x→∞ \begin{array}{l}\frac{2x^2}{\left(x^2-4\right)}\\\end{array}
= lim x→∞ \begin{array}{l}\frac{\displaystyle\frac{2x^2}{x^2}}{\left(1-{\displaystyle\frac4{x^2}}\right)}\\\end{array}
= 2
තිරස් ස්පර්ශෝන්මුඛ : y = 2
(x අනන්තයට යන විට y ගේ අගය)
සිරස් ස්පර්ශෝන්මුඛ : x = 2 හෝ x = -2

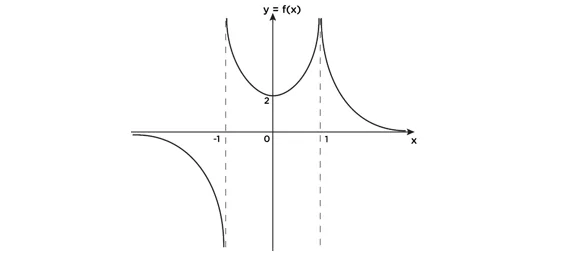
උදා: (15) x≠±1 සඳහා \text{f(x)=}\frac a{\left(\text{x-1}\right)^2}\text{+}\frac b{\left(\text{x+1}\right)}යැයි ගනිමු. a, b තාත්වික නියත වේ. y = f(x) ප්රස්තාරයට (0,2) හිදී හැරුම් ලක්ෂ්යයක් ඇති බව දී ඇත. a , b සොයා, (0,2) යනු එකම හැරුම් ලක්ෂ්යය බව පෙන්වන්න. හැරුම් ලක්ෂ්යය හා ස්පර්ශෝන්මුඛ පැහැදිලිව දක්වමින් y = f(x) හි ප්රස්තාරයේ දළ සටහනක් අඳින්න. එනයින් |f(x)| ප්රස්තාරයේ දළ සටහනක් අඳින්න.
- \text{f(x)=}\frac a{\left(\text{x-1}\right)^2}\text{+}\frac b{\left(\text{x+1}\right)}
- \begin{array}{l}\text{f'(x)=}\frac{\left(\text{x+1}\right)^2\left(0\right)\text{-a}\left(2\right)\left(\text{x+1}\right)}{\left(\text{x+1}\right)^4}\text{+}\frac{\left(\text{x+1}\right)\left(0\right)-b\left(1\right)}{\left(\text{x+1}\right)^2}\\\text{ =}\frac{-2a}{\left(\text{x+1}\right)^3}\text{-}\frac b{\left(\text{x+1}\right)^2}\end{array}
x = 0 විට, f’(x) = 0
\begin{array}{l}\frac{-2a}{\left(\text{x+1}\right)^3}\text{-}\frac b{\left(\text{x+1}\right)^2}\text{=0}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{-2a}{-1}-\frac b1=0\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2a=b\end{array}x = 0 විට, y = 2 වේ. [හැරුම් ලක්ෂ්යය (0,2) බව දී ඇත.]
\text{f(x)=}\frac a{\left(\text{x-1}\right)^2}\text{+}\frac b{\left(\text{x+1}\right)}2 = a / ( 0 -1)2 + b/(0+1)
2 = a/1 + b/1
2 = a+2a
a = 2/3
b = 4/3
\begin{array}{l}\text{f}^\iota\text{(x)=}\frac{\text{(}\frac{-4}3\text{)}}{(x-1)^3}\text{-}\frac{\text{(}\frac43\text{)}}{(x+1)^2}\\\\\text{f}^\iota\text{(x)=}\frac{\text{(}\frac{-4}3\text{)}\left[\left(x+1\right)^2\text{+}\left(x-1\right)^3\right]}{(x-1{)^3(x+1)^2}}\\\text{f}^\iota\text{(x)=}\frac{\text{(}\frac{-4}3\text{)}\left(x^3-2x^2+6x\right)}{(x-1{)^3(x+1)^2}}\\\text{f}^\iota\text{(x)=}\frac{\text{(}\frac{-4}3\text{)}\left(x\right)\left(x^2-2x+6\right)}{(x-1{)^3(x+1)^2}}\end{array}(+)
\text{f}^\iota\text{(x)=}\frac{\text{(}\frac{-4}3\text{)}\left(x\right)\overbrace{\left[\left(x-1\right)^2+4\right]}}{(x-1{)^3(x+1)^2}}[(x-1)2+4 තුළින් (+) පිළිතුරක් ලැබේ.]
එමනිසා මේ සඳහා තිබිය හැක්කේ එක ස්තාවර ලක්ෂ්යයක් පමණි. (0,2)


(0, 2 ) අවම ලක්ෂ්යයකි.
lim x→ ∞ f(x) = lim x→∞ \frac a{\left(x-1\right)^2}+\frac b{\left(x+1\right)}
= limx→∞ \begin{array}{rcl}&&\frac{\left(2/3\right)(x+1)+\left(4/3\right)(x-1)^2}{(x-1)^2(x+1)}\\\\\end{array}
lim x→ +∞ y = 0 lim x→- ∞ y = 0
තිරස් ස්පර්ශෝන්මුඛ : y = 0
සිරස් ස්පර්ශෝන්මුඛ : x = 1 හෝ x = -1
Lim x→ -1– y = -∞ limx→1– y = +∞
Lim x→ -1+ y = -∞ limx→1+ y = +∞

උදා: (16.) y=\frac{\displaystyle\left(3x+3\right)}{x\left(x-3\right)}
\begin{array}{rcl}y\;=\;\frac{\displaystyle3(x+1)}{x(x-3)};\;\;\;x\neq\;0,3\\\frac{\displaystyle dy}{\displaystyle dx}&=&\frac{\displaystyle x(x-3)(3)-(3x+3)(2x-3)}{{x(x-3)}^2}\\\frac{\displaystyle dy}{\displaystyle dx}&=&\frac{(3x^2-9x-6x^2+9x-6x+9)}{{x(x-3)}^2}\\\frac{\displaystyle dy}{\displaystyle dx}&=&\frac{\;-3x^2-6x+9}{(x^2-\;3x)\;^2}\\\frac{\displaystyle dy}{\displaystyle dx}&=&\frac{-3(x^2+2x+3)}{(x^2-\;3x)\;^2}\\\frac{\displaystyle dy}{\displaystyle dx}&=&\frac{\displaystyle-3(x+3)\;(x-1)}{(x^2-\;3x)\;^2}\\\\\\\end{array}ස්තාවරලක්ෂ්ය සඳහා,
\frac{dy}{dx}= 0
\frac{\displaystyle-3\left(x+3\right)\left(x-1\right)}{\left(x^2-3x\right)^2}=0 = 0
x+3 = 0 හෝ x-1 = 0
x = -3 හෝ x = 1
x = -3 විට , y = (3x-3+3)/-3(-3-3)
y = -6/18
y = -1/3
x = 1 විට, y = 6 / (-2)
y =-3


Lim x→3– y = -∞ limx→0– y = +∞
Lim x→3+ y = +∞ limx→0+ y = -∞
Lim x→ ∞ y = lim x→∞ \begin{array}{rcl}&&\frac{(3x+3)}{x(x-3)}\\\\\end{array}
= lim x→∞ \begin{array}{rcl}&&\frac{x\left(3+{\displaystyle\frac3x}\right)}{x^2\left(1-{\displaystyle\frac3x}\right)}\\\\\end{array}
=0
තිරස් ස්පර්ශෝන්මුඛ : y = 0
සිරස් ස්පර්ශෝන්මුඛ : x = 0 හෝ x = 3

එමනිසා මෙය වැඩිවන නතිවර්තයකි.

