
වර්ගජ සමීකරණ ක්රි.පූ.2000 ක තරම් පැරණි ඉතිහාසයකට උරුමකම් කියන බවට බැබිලෝනියනු මැටි පුවරු කදිම සාක්ෂ්යකි. බැබිලෝනියනුවන් ඍජුකෝණාස්රාකර වර්ගඵලයන් ගණනය කිරීමේදී x+y=p හා xy=q ආකරයේ සමගාමී සමීකරණ දෙකක අනුබද්ධයෙන් x= ලෙස ගොඩනගා ගත් අතර එය z2+q=pz පරිදි නූතන වර්ගජයක ස්වරූපය ගත් සමීකරණයේ z හි මූල වන x හා y හි සූත්ර ලෙස ව්යුත්පන්න කරන ලදී. කාලයාගේ ඇවෑමෙන් දාර්ශනික මතවාද හමුවේ පරිණාමනය වෙමින් az2+bz+c=0 වූ වර්ගජයක මූල ලෙස විසදුම් අවස්ථා දෙකක් දක්වා වර්ධනය වීම ගණිත ඉතිහාසයේ සුවිශේෂී සන්ධිස්ථානයක් විය.
සංයුක්ත ගණිතය 1 (ශුද්ධ ගණිතය )ප්රශ්න පත්රයේ B කොටසේ (රචනා ප්රශ්න )11 ගැටළුවේ අඩංගු වන්නේ මෙම පාඩමේ අඩංගු සිද්ධාන්ත වේ.
- a,b,c නියත වන, ax2+bx2+c=0 යනු x හි වර්ගජ සමීකරණයයි. මෙහි a≠0 වීම අනිවාර්ය වේ.
වර්ගජ සමීකරණයක මූල වල ස්වභාවය විවරණය (ජ්යාමිතික ක්රමය)
ax2+bx2+c=0 ———(1)
(1) හි මූල යනු,
y = ax2+bx+c ශ්රිතයේ හා y=0 රේඛාවේ (එනම් x අක්ෂයේ) ඡේදනය වන ලක්ෂ්යවලට අනුරූප x ඛණ්ඩාංක වේ.
b2-4ac>0 විට,
a>0,
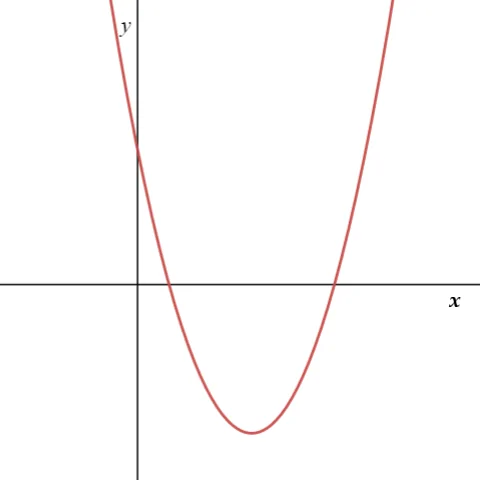
a<0,
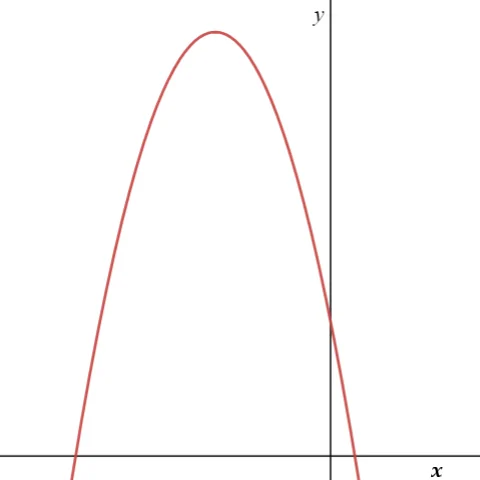
මෙවිට, y = ax2+bx+c ශ්රිතයේ ප්රස්තාරය හා y = 0 රේඛාව ප්රභින්න ලක්ෂ්ය දෙකකදී ඡේදනය වේ.∴මෙවිට ①සමීකරණයට තාත්වික සංඛ්යා රේඛාවේ පවතින හා එකිනෙකට වෙනස් විසඳුම් දෙකක් පවතී.
එනම්,① හි මූල තාත්වික හා ප්රභින්න වේ යැයි කියනු ලැබේ.
b2 – 4ac = 0 විට,
a>0,
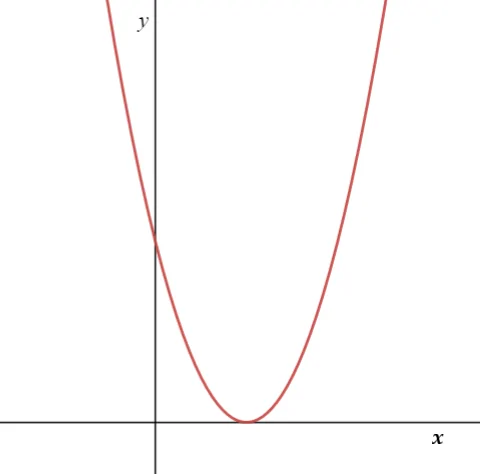
a<0,
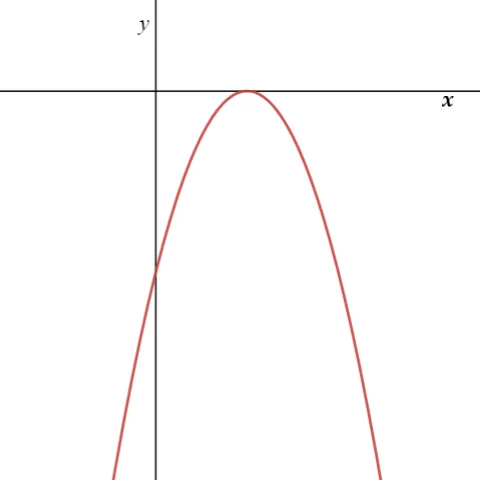
මෙහිදී y = ax2+bx+c ප්රස්තාරය සහ y=0 රේඛාව ස්පර්ශ වේ.එනම්,සමපාත ලක්ෂ්ය දෙකකදී ඡේදනය වේ.∴මෙවිට ax2+bx+c=0 සමීකරණයට තාත්වික සංඛ්යා රේඛාවේ විසඳුම් දෙකක් පවතින අතර ඒවා එකිනෙකට සමාන වේ යැයි කියනු ලැබේ.
එනම්,① හි මූල තාත්වික හා සමපාත වේ යැයි කියනු ලැබේ.
b2-4ac < 0 විට,
a>0,
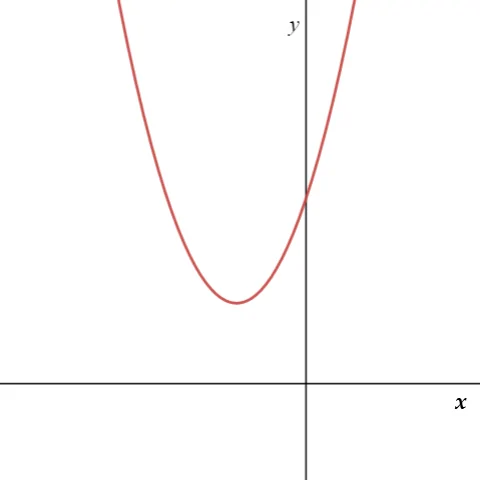
a<0,
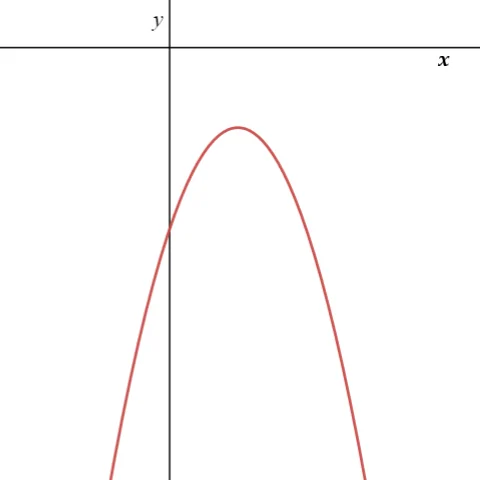
මෙවිට y = ax2+bx+c ශ්රිතයේ ප්රස්තාරය හා y = 0 රේඛාව ඡේදනය වන්නේ හෝ ස්පර්ශ වන්නේ නැත.∴මෙවිට ① සමිකරණයේ මූල තාත්වික සංඛ්යා රේඛාවේ නොපවතී.
එනම්,① හි මූල අතාත්වික වේ යැයි කියනු ලැබේ.
ax2+bx2+c=0 සමිකරණයේ මුල වල ස්වභාවය පැහැදිලි කිරීම (වීජීය ක්රමය)
\begin{array}{rcl}ax^2+bx^2+c&=&0\rightarrow(1)\;\\x^2+\left(\frac ba\right)\;x+\left(\frac ca\right)\;&=&0\;\\\\\left(x+\frac b{2a}\right)^2-\left(\frac b{2a}\right)^2+\frac ca&=&0\;\\\\\left(x+\frac b{2a}\right)^2\;&=&\;\left(\frac b{2a}\right)^2-\left(\frac ca\right)\\\\&=&\;\frac{b^2-4ac}{4a^2}\\\\x+\frac b{2a}\;&=&\;\frac{\pm\sqrt{b^2-4ac}}{2a}\;\\\\x&=&\;\frac{-b\pm\sqrt{b^2-4ac}}{2a}\end{array}
b2 – 4ac > 0 විට,
\begin{array}{rcl}\;\;\;\;b^2-4ac&=&k^2\;\;\;\;\;\;k\neq0\\x&=&\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\&=&\frac{-b\pm k}{2a}\end{array}
\begin{array}{l}{x=\frac{-b+k}{2a}\;\text{හෝ }x=\frac{-b-k}{2a}}\\\\\end{array}
මේ අනුව, x සඳහා තාත්වික සංඛ්යා රේඛාවේ පවතින හා එකිනෙකට වෙනස් විසඳුම් දෙකක් ලැබේ.
එනම්,① හි මූල තාත්වික හා ප්රභින්න වේ යැයි කියනු ලැබේ.
b2–4ac=0
- එවිට, k = 0 වේ.
\begin{array}{rcl}x&=&\frac{-b\pm\sqrt{\;b^2-4ac}}{2a}\\&&\\x&=&\frac{-b\pm0}{2a}\\&&\\x=\frac{-b}{2a}\;&\text{හෝ}&x=\frac{-b}{2a}\end{array}
x සඳහා ලැබෙන අගයයන් තාත්වික සංඛ්යා රේඛාවේ පවතින අතර,ඒවා එකිනෙකට සමාන වේ.
එනම්,① හි මූල තාත්වික හා සමපාත වේ යැයි කියනු ලැබේ.
b2 – 4ac < 0 විට,
\begin{array}{rcl}b^2-4ac&=&-k^2\;,\;k\neq0\\x&=&\frac{-b\pm\sqrt{-k^2}}{2a}\end{array}
\sqrt{-k^2} සඳහා අගයයන් තාත්වික සංඛ්යා රේඛාවේ නොපවතී. ∴මෙහිදී x සඳහා ලැබෙන අගයයන් තාත්වික සංඛ්යා රේඛාවේ නොපවතී.
එනම්,① හි මූල අතාත්වික වේ යැයි කියනු ලැබේ.
මේ අනුව, ax2+bx+c = 0 සමීකරණයේ මූලවල ස්වභාවය තීරණය කරන රාශිය b2 – 4ac වේ.
∴ එය එම වර්ගජ සමීකරයේ විවේචකය ලෙස හඳුන්වනු ලැබේ.එය △ මඟින් එය සංකේතවත් කරයි.
ax2+bx+c=0
△= b2-4ac
- △>0 නම්, සමිකරණයේ පවතින මූල තාත්වික හා ප්රභින්න වේ.
- △=0 නම්, සමිකරණයේ මූල තාත්වික හා සමපාත වේ.
- △<0 නම්, සමිකරණයේ මූල අතාත්වික වේ.
උදා:- (1.)පහත සමීකරණවල මූල ගැන කුමක් කිව හැකිද?
- (x-a)(x-b) – k2 = 0
\begin{array}{rcl}\left(x-a\right)\left(x-b\right)-k^2\;&=&\;0\\x^2-x\left(a+b\right)+ab-k^2\;&=&\;0\\\Delta\;&=&\;b^2-4ac\\&=&\;\left[-\left(a+b\right)^2\right]\;-\;4\cdot1\left(a\cdot b-k^2\right)\\&=&\;a^2+b^2-2ab+4k^2\\&=&\;\left(a-b\right)^2+4k^2\\&&\end{array}
\begin{array}{rcl}\text{සියළු}\;a,b\;\text{සඳහා,}\;\;\left(a-b\right)^2&\geq&0\;\text{වේ.}\\4k^2&\geq&0\;\text{වේ.}\\\left(a-b\right)^2+4k^2&\geq&0\\\triangle&\geq&0\;\text{වේ.}\\&&\end{array}
එනම්,a,b,k සියලු අගයයන්ට ඉහත සමීකරණය සඳහා තාත්වික මූල පවතී. a = b හා k=0 විට මූල සමාන වේ.අනෙක් හැම විටම ප්රභින්න මූල පවතී.
- 2x2 – 2(a + b + c)x +ab + bc + ca = 0
\begin{array}{rcl}\triangle\;&=&\;b^2-4ac\\&=&\;\left[-2\left(a+b+c\right)\right]^2-4\times2\left(ab+bc+ca\right)\\&=&\;4\left[\left(a+b+c\right)^2-2\left(ab+bc+ca\right)\right]\\&=&\;4\left(a^2+b^2+c^2+2ab+2bc+2ca-2ab-2bc-2ca\right)\\&=&\;4\left(a^2+b^2+c^2\right)\\a^2&\geq&0\\b^2&\geq&0\\c^2&\geq&0\\a^2+b^2+c^2&\geq&0\\\triangle&\geq&0\end{array}
a,b,c සියලුම අගයයන්ට සමීකරණයේ මූල සෑමවිටම තාත්වික වේ.
a,b,c = 0 විට,මූල සමාන වේ.අනෙක් හැම විටම මූල ප්රභින්න වේ.
උදා:- (2.) ax2+bx2+c = 0 සමීකරණයේ මූල තාත්වික විට පහත සමීකරණයේ මූලවල ස්වභාවය සොයන්න.මෙහි,a≠0 වේ.
\begin{array}{rcl}a^2x^2+4abx+b^2+2ac\;&=&\;0\\\triangle\;&=&\;\left(4ab\right)^2-4a^2\left(b^2+2ac\right)\\&=&\;16a^2b^2-4a^2b^2+8a^3c\\&=&\;12a^2b^2-8a^3c\\&=&\;4a^2\left(3b^2-2ac\right)\\&=&\;2a^2\left(6b^2-4ac\right)\\&=&\;2a^2\left(5b^2+b^2-4ac\right)\end{array}
ax2+bx2+c = 0 සමීකරණයේ මූල තාත්වික නිසා, b2 – 4ac ≥ 0 වේ.
a2 ≥ 0 වේ. b2 ≥ 0 ද, b2 – 4ac ≥ 0 ද නිසා,
\begin{array}{rcl}\left(5b^2+b^2-4ac\right)&\geq&0\;\text{වේ.}\\\;2a^2\left(5b^2+b^2-4ac\right)&\geq&0\;\text{වේ.}\\\text{එනම්, }\triangle&\geq&0\;\text{වේ.}\\&&\end{array}
∴සමීකරණයට තාත්වික මූල පවතී.
b = 0 හා b2 – 4ac = 0 විට,එනම් b = 0 හා 4ac = 0 විට,එනම් b = 0 හා c = 0 විට,සමපාත මූල පවතී.
අනෙක් හැම විටම මූල ප්රභින්න වේ.
උදා:- (3.) x තාත්වික නම්, x+\frac1x ට -2 හා +2 අතර කිසිම අගයක් ගත නොහැකි බව පෙන්වන්න.
\begin{array}{rcl}x+\frac1x&=&k\;\;\;,\;\;\;x\in\mathbb{R}\\x^2-kx+1&=&0\\&{}&{}\\x\text{ තාත්වික නිසා },\;\;\;\triangle\;\;&\geq&\;0\\\left(-k\right)^2-4\cdot1\cdot1&\geq&0\\k^2-4&\geq&0\\\left(k-2\right)\left(k+2\right)&\geq&0\\k\leq-2\;&\text{හෝ}&\;k\;\geq\;2\end{array}
\\x+\frac1x=k\;\text{නිසා},\;x+\frac1x\;\text{ට}\;-2\;\text{හා}\;+2\;\text{අතර අගයයක් ගත නොහැක.}
ax2+bx2+c = 0 ⤇ ①
x = α ; ① හි මූලයක් ලෙස ගනිමු.
එවිට , x-α යනු f(x)= ax2+bx+c බහු පදයේ සාධකයක් වේ.
එවිට,f(α) = 0 වේ. aα2+bα+c = 0 වේ.
ax2+bx+c=0 සමීකරණයේ x = α මූලයක් විට,
aα2+bα+c=0 වේ.
උදා :- (1.) x = 1 යනු k( x2 + x + 1) + x2 -3x + 1 = 0 සමීකරණයේ මූලයකි.k සොයන්න.
\begin{array}{rcl}k\left(x^2+x+1\right)+x^2-3x+1\;&=&\;0\\x\;=\;1\;\text{මූලයක් නිසා,}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\k(1^2+1+1)+1^2-3\cdot1+1\;&=&\;0\\3k\;–\;1\;&=&\;0\\k\;&=&\;\frac13\end{array}
උදා :- (2.) ax2 + bx + c = 0 සමීකරණයේ එක් මූලයක් අනෙක මෙන් දෙගුණයක් වීමට තිබිය යුතු අවශ්යතාවය කුමක්ද?
ax2+bx2+c = 0
\begin{array}{rcl}\text{මෙහි මූල}\;\alpha\;\text{හා}\;2\alpha\;\text{වේ}.\;\alpha\;\text{මූලයක් නිසා},\\a\alpha^2+b\alpha+c\;&=&\;0\;\;\;⤇①\\2\alpha\;\text{මූලයක් නිසා},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\a(2\alpha)^2+b(2\alpha)+c\;&=&\;0\\4a\alpha^2\;+\;2b\alpha\;+\;c\;\;\;\;\;&=&\;0\;\;\;\;⤇②\end{array}
\begin{array}{rcl}①\cdot4-②\text{න්},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\2b\alpha+3c&=&0\\\alpha&=&-\frac{3c}{2b}\\①\text{න්},\;\;\;\;\;a\left(-\frac{3c}{2b}\right)^2+b\left(-\frac{3c}{2b}\right)+c&=&0\\\frac{9ac^2}{4b^2}-\frac{3c}2+c&=&0\\9ac&=&2b^2\end{array}
විචල්ය දෙකක් තියෙන මේ සමීකරණය විසඳලා (x+y)2 හි අගය සොයන්න ඔයාලටත් පුළුවන්ද බලන්න.
(x+\sqrt{1+x^2})\;(y+\sqrt{1+y^2})\;=\;1
වර්ගජ සමීකරණයක මූලවල එකතුව සහ ගුණිතය එහි සංගුණක මගින් ප්රකාශ කිරීම
ax2+bx2+c = 0 ⤇ ①
① හි මූල α හා β ලෙස ගනිමු.
විලෝමව, α,β මූල වන x හි වර්ගජ සමීකරණය,
\begin{array}{rcl}(x\;–\;\alpha)(x\;–\;\beta)&=&0\;\text{වේ}.\\x^2\;–(\alpha+\beta)x+\alpha\beta\;&=&\;0\;\;⤇②\end{array}
① හා ② ට එකම මූල පවතී.
∴① හා ② සමීකරණ සර්වසම වේ.
∴ඒවායේ අනුරූප පදවල සංගුණක අතර අනුපාත සමාන වේ.
\begin{array}{rcl}\frac a1&=&\frac b{-\left(\alpha+\beta\right)}=\frac c{\alpha\beta}\\\frac a1&=&\frac b{-\left(\alpha+\beta\right)}\;\;\;\text{නිසා,}\;\;\;\alpha+\beta=-\frac{\displaystyle b}a\;\text{වේ.}\\\frac{\displaystyle a}{\displaystyle1}&=&\frac{\displaystyle c}{\displaystyle\alpha\beta}\;\;\;\text{නිසා,}\;\;\;\alpha\beta=\frac{\displaystyle c}a\text{වේ.}\end{array}
ax2+bx+c=0
මූල α හා β වන විට,
\begin{array}{rcl}{(\alpha+\beta)}&=&-\left(\frac ba\right)\\&&\\&&\end{array}
\begin{array}{rcl}\alpha\beta&=&\left(\frac ca\right)\end{array}
අමතර දැනුමට,
ax3 + bx2 + cx + d = 0
මූල α,β හා γ නම්,
\begin{array}{rcl}\alpha+\beta+\gamma\;&=&\;-\frac ba\\\alpha\cdot\beta\cdot\gamma\;&=&\;-\frac da\\\alpha\beta\;+\;\beta\gamma\;+\;\alpha\gamma\;&=&\;\;\frac ca\end{array}
α හා β හි සමමිතික ප්රකාශන
\begin{array}{rcl}&&\frac\alpha\beta+\frac\beta\alpha\\\\&&\alpha^3+\beta^3\\\\&&\frac\beta{\alpha^2+1}+\frac\alpha{\beta^2+1}\end{array}
ඉහත ප්රකාශනවල α හා β අකුරු මාරු කළ විට ප්රකාශනයේ වෙනසක් නැත.එවැනි ප්රකාශනයක් α හා β හි සමමිතික ප්රකාශනයක් වේ.
එවැනි ප්රකාශන α + β හා αβ පද ඇසුරෙන් ප්රකාශ කළ හැක
- \frac\alpha\beta+\frac\beta\alpha=\frac{\alpha^2+\beta^2}{\alpha\beta}=\frac{\left(\alpha+\beta\right)^2-2\alpha\beta}{\alpha\beta}
- \alpha^3+\beta^3=\left(\alpha+\beta\right)^3-3\alpha\beta\left(\alpha+\beta\right)
- \begin{array}{rcl}\frac\beta{\alpha^2+1}+\frac\alpha{\beta^2+1}\;&=&\;\frac{\beta\left(\beta^2+1\right)+\alpha\left(\alpha^2+1\right)}{\left(\beta^2+1\right)\left(\alpha^2+1\right)}\\&=&\;\frac{\alpha^3+\beta^3+\alpha+\beta}{\alpha^2\beta^2+\alpha^2+\beta^2+1}\\&=&\;\frac{(\alpha+\beta)^3-3\alpha\beta(\alpha+\beta)+(\alpha+\beta)}{(\alpha\beta)^2+(\alpha+\beta)^2-2\alpha\beta+1}\end{array}
ax2+bx2+c = 0 සමීකරණයට තාත්වික මූල ඇත.
∴Δ ≥ 0
b2 – 4ac ≥ 0
මෙම සමීකරණයේ මූල α හා β යැයි ගනිමු.
i. මූල දෙකම + වීමට නම්,
\begin{array}{rcl}\alpha+\beta&=&-\frac ba\\\alpha.\beta&=&\frac ca\end{array}
\begin{array}{rcl}\alpha\;\text{හා}\;\beta\;\text{දෙකම}\;+\;\text{වේ නම්},\;\;\;\;\alpha+\beta&>&0\;\text{හා}\;\alpha\cdot\beta\;>\;0\;\text{වේ}.\\\\-\frac ba&>&0\;\text{හා}\;\frac ca\;>\;0\;\text{වේ}.\\\\\text{එනම්,}\;\;\frac ba&<&0\;\text{හා}\;\frac ca\;>\;0\;\text{වේ}.\end{array}
එනම්,එවිට aහා c සෑමවිටම එකම ලකුණ ගනී.b ඊට ප්රතිවිරුද්ධ ලකුණ ගනී.
ii. මූල දෙකම – වීමට නම්,
\begin{array}{rcl}\alpha+\beta&=&-\frac ba\\\alpha.\beta&=&\frac ca\end{array}
\begin{array}{rcl}\alpha\;\text{හා}\;\beta\;\text{දෙකම}\;-\;\text{වේ නම්},\;\;\;\;\alpha+\beta&<&0\;\text{හා}\;\alpha\cdot\beta\;>\;0\;\text{වේ}.\\\\-\frac ba&<&0\;\text{හා}\;\frac ca\;>\;0\;\text{වේ}.\\\\\text{එනම්,}\;\;\frac ba&>&0\;\text{හා}\;\frac ca\;>\;0\;\text{වේ}.\end{array}
එනම්, a, b හා c තුනටම එකම ලකුණ පවතී.
iii. එක් මූලයක් + හා අනෙක (-) විට,
\begin{array}{l}\alpha+\beta\text{ හි ලකුණ ගැන නිශ්චිතව කිව නොහැක}.\\\alpha\cdot\beta<0\;\text{වේ. එනම්,}\;\;\frac ca<0\;\text{වේ.}\end{array}
එනම්, a හා cට ප්රතිවිරුද්ධ ලකුණු ඇත.b ඕනෑම අගයකි.
iv. මූල දෙකම ශුන්ය වීමට,
\begin{array}{rcl}\alpha+\beta\;&=&\;0\\\alpha\cdot\beta\;&=&\;0\\\\\frac ba=0\;\;&\text{හා}&\;\;\frac ca=0\;\text{වේ.}\\b\;\;=&c&=\;\;0\;\;\text{වේ.}\end{array}
v. එක් මූලයක් පමණක් ශුන්ය වීමට,
\begin{array}{rcl}\alpha+\beta\;&≠&\;0\\\alpha\cdot\beta\;&=&\;0\\\\-\frac ba\neq0\;\;&\text{හා}&\;\;\frac ca=0\;\text{වේ.}\\b\;\;\neq&c&=\;\;0\;\;\text{වේ.}\end{array}
උදා :- (1.) ax2+bx2+c = 0 සමීකරණයේ එක් මූලයක් අනික මෙන් දෙගුණයකි.a,b,c අතර සම්බන්ධතාවය සොයන්න.
ax2+bx2+c = 0 ⤇①
මූල α හා 2α වේ යැයි ගනිමු.
\begin{array}{rcl}\alpha\;+\;2\alpha\;&=&\;-\frac ba\\3\alpha\;&=&\;-\frac ba\\\alpha\;&=&\;-\frac b{3a}\end{array}
\begin{array}{rcl}\alpha\cdot2\alpha\;&=&\;\frac ca\\[4px]2\alpha^2\;&=&\;\frac ca\\[4px]\alpha^2\;&=&\;\frac c{2a}\end{array}
\begin{array}{rcl}\left(-\frac b{3a}\right)^2\;&=&\;\frac c{2a}\\[4px]\frac{b^2}{9a^2}\;&=&\;\frac c{2a}\\[4px]2b^2\;&=&\;9ac\end{array}
උදා:- (2.) ax2+bx2+c = 0 සමීකරණයේ මූල α හා β වේ. α4 හා β4 මූල වශයෙන් ඇති වර්ගජ සමීකරණය සොයන්න.
ax2+bx2+c = 0 සමීකරණයේ මූල α හා β නිසා,
\begin{array}{rcl}\alpha+\beta&=&-\frac ba\\\alpha\cdot\beta\;&=&\;\frac ca\;\end{array}
α4 හා β4 මූල වශයෙන් ඇති වර්ගජ සමීකරණය:-
\begin{array}{rcl}(x-\alpha^4)(x-\beta^4)&=&0\\[4px]x^2–(\alpha^4+\beta^4)x+\alpha^4\beta^4&=&0\end{array}
\begin{array}{rcl}\alpha^2+\beta^2&=&(\alpha+\beta)^2-2\alpha\beta=\left(-\frac ba\right)^2–\frac{2c}a=\frac{b^2-2ac}{a^2}\\\alpha^4+\beta^4&=&{(\alpha^2+\beta^2)^2-2\alpha^2\beta^2=\left(\frac{b^2-2ac}{a^2}\right)^2-2\left(\frac ca\right)^2}\end{array}
අවශ්ය සමීකරණය :-
\begin{array}{rcl}x^2-\left[\left(\frac{b^2-2ac}{a^2}\right)^2-2\left(\frac ca\right)^2\right]x+\frac{c^4}{a^4}&=&\;0\end{array}
ax2+bx2+c = 0 සමීකරණයේ මූල α හා β වන විට α හා β හි ඒකජ සංයෝජන මූල ලෙස ඇති සමීකරණ සෙවීමේ කෙටි ක්රම
ax2+bx2+c = 0 සමීකරණයේ මූල α හා β වේ. (2α + 3) හා (2β + 3) මූල වශයෙන් ඇති සමීකරණය සෙවීම.
ක්රමය 1
(2α+3) හා (2β+3) මූල වශයෙන් ඇති සමීකරණය :-
\begin{array}{rcl}\lbrack x-(2\;\alpha\;+\;3)\rbrack\lbrack x-(2\beta+3)\rbrack\;&=&\;0\;\\[4px](x–3-2\alpha)(x–3-2\beta)\;\;&=&\;0\\[4px](x\;–\;3)^2\;–\;2(\alpha+\beta)\;(x\;–\;3)\;+\;4\alpha\beta\;&=&\;0\\[4px](x\;–\;3)^2\;–\;2\left(-\frac ba\right)(x\;–\;3)\;+4\frac ca\;&=&\;0\\[4px]a(x\;–\;3)^2+2b(x\;–\;3)+4c\;\;&=&\;0\\[4px]ax^2+2(b–3a)x+9a–6b+4c\;&=&\;0\\&&\end{array}
ක්රමය 2
x = 2α + 3 ලෙස ගනිමු.
\alpha\;=\;\frac{x-3}{2\alpha} වේ.
α යනු ax2+bx2+c = 0 සමීකරණයේ මූලයක් නිසා,
aα2+bα+c = 0
(2α+3) හා (2β+3) මූල වශයෙන් ඇති සමීකරණය :-
\begin{array}{rcl}a\left(\frac{x-3}2\right)^2+b\left(\frac{x-3}2\right)+c\;&=&\;0\\\\a(x–3)^2+2b(x–3)+4c\;&=&\;0\end{array}
ax2+bx2+c = 0 සමීකරණයේ මූල α හා β වේ.\;\left(\alpha\;+\;\frac1\beta\right)\;\text{හා}\;\left(\beta\;+\;\frac1\alpha\right)\; මූල වශයෙන් ඇති සමීකරණය සෙවීම.
ක්රමය 1
\;\left(\alpha\;+\;\frac1\beta\right)\;\text{හා}\;\left(\beta\;+\;\frac1\alpha\right)\; මූල වශයෙන් ඇති සමීකරණය:-
\begin{array}{rcl}\left[x-\left(\alpha\;+\;\frac1\beta\right)\right]\left[x-\left(\beta\;+\;\frac1\alpha\right)\right]\;&=&\;\;0\\(\beta x\;–\;\alpha\beta\;–\;1)\;(\alpha x\;-\;\alpha\beta\;–\;1)\;&=&\;0\\\alpha\beta x^2–(\alpha\;+\;\beta)(\alpha\beta\;+\;1)x+(\alpha\beta\;+\;1)^2\;&=&\;0\\\frac cax^2\;-\;\left(-\frac ba\right)\left(\frac ca+1\right)x+\left(\frac ca+1\right)^2\;&=&\;0\\acx^2\;+\;b(a\;+\;c)x\;+\;(a\;+\;c)^2\;\;\;&=&\;0\end{array}
ක්රමය 2
\begin{array}{rcl}x\;&=&\;\alpha\;+\;\frac1\beta\;\;\;\;\text{ලෙස ගනිමු.}\;\\[4px]\beta x\;&=&\;\alpha\beta+1\\[4px]&=&\;\frac ca+1\\[4px]\beta\;&=&\;\frac{a+c}{ax}\\\\\beta\;\text{යනු}\;ax^2+bx^2+c\;&=&\;0\;\text{සමීකරණයේ මූලයක් නිසා,}\;\\a\beta^2+b\beta+c\;\;&=&\;0\end{array}
\;\left(\alpha\;+\;\frac1\beta\right)\;\text{හා}\;\left(\beta\;+\;\frac1\alpha\right)\; මූල වශයෙන් ඇති සමීකරණය:-
\begin{array}{rcl}a\left[\frac{a+c}{ax}\right]^2+\;b\left[\frac{a+c}{ax}\right]+\;c\;&=&\;0\\[4px](a+c)^2+b(a+c)x+acx^2\;&=&\;0\\[4px]acx^{2\;}{+b(a+c)x+}\;{(a+c)^2}\;\;&=&\;0\end{array}
“The essence of Mathematics is not to make simple things complicated,but to make complicated things simple“
Stan Gudder
(Mathematician)
Video Links :

