04.04.00 -අවකලනය ව්‍යුත්පන්න වල භාවිත

සං‍යුක්ත ගණිතය I (ශුද්ධ ගණිතය) ප්‍රශ්න පත්‍රයේ A කොටසේ ගැටලුවක හා B කොටසේ 14 වැනි ගැටලුවෙහි අඩංගු වන්නේ මෙම පාඩමෙහි සිද්ධාන්ත වේ.

උදා: (22.)    රූපයේ දැක්වෙන්නේ ආභරණ සුරැකුම් පෙට්ටියක අනුරුවකි. එය උස h වූ සිලින්ඩරයක් හා එහි   දෙකෙළවරට සම්බන්ධ කරන ලද අරය r වූ කුහර අර්ධ ගෝල දෙකකින් සමන්විතය.

1. පෙට්ටියේ පරිමාව V සහ බාහිර පෘෂ්ඨ වර්ගඵලය S සඳහා ප්‍රකාශන h හා r ඇසුරින් ලබාගන්න.
2. V = 36π නම් s = 72π/r + 4πr²/3 බව පෙන්වන්න.
3. S හි අවම අගය 36π බව පෙන්වන්න.

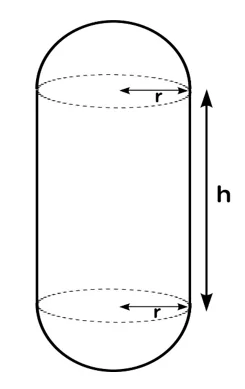
1. V=4πr³/3 + πr²h

S= 2πrh  + 4πr²

ii. V=36π

 4πr³/3 + πr²h = 36π

                   πr²h = 36π – 4πr³/3

                          h =\frac{\left[3\left(36\mathrm\pi\right)-4\mathrm{πr}^3\right]}{3\mathrm{πr}}

                          h = (108-4r³)/3r²

                          h = 36/r² – 4r/3

                  S = 2πrh+4πr²

                 S = 2πr (36/r² – 4r/3) + 4πr²

                 S = 72π/r – 8πr²/3 + 4πr²

                 S = 72π/r + 4πr²/3

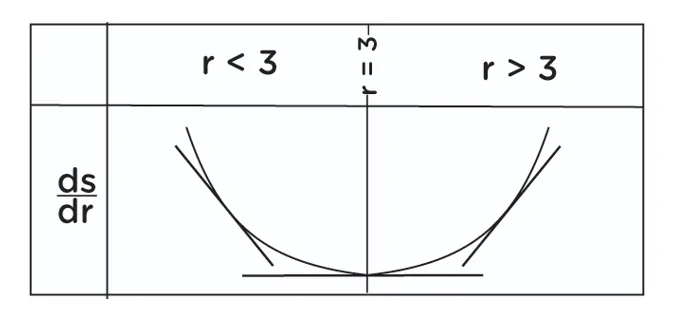
iii.S, r විශයෙන් අවකලනය කිරිම,

\begin{array}{rcl}&&\frac{ds}{dr}\end{array}= {r(0)-72π(1)}/r² + {3(4π)(2r)-4πr²(0)}/9

                     \begin{array}{rcl}&&\frac{ds}{dr}\end{array} = -72π/r² + 24πr/9

                     \begin{array}{rcl}&&\frac{ds}{dr}\end{array}= 24π (-3/r² + r/9)

ස්තාවර ලක්ෂ්‍ය සඳහා,

               \begin{array}{l}\frac{ds}{dr}\end{array}= 0 විය යුතුය.

\begin{array}{rcl}&&\frac{ds}{dr}\end{array}= 0

24π (-3/r² + r/9) = 0

                          r/ 9 = 3/r²

                             r³ = 27

                               r = 3

     S = 72π/r + 4πr²/3

     S = 72π/3 + 4π (9)/3

     S= 36π

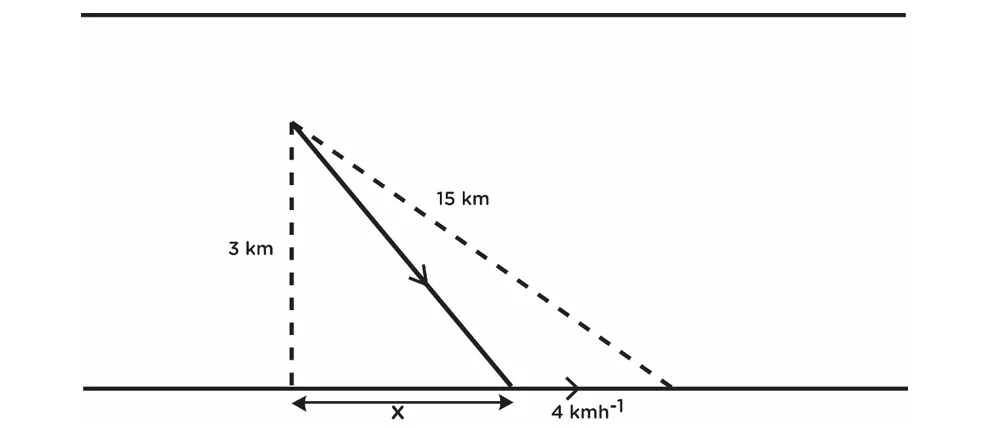
උදා: (23.)    මිනිසෙක් ගඟක සෘජු ඉවුරට 3 km දුරින් නිශ්චල ජලයේ තිබෙන බෝට්ටුවක සිටියි. ඔහු සිටින එම ස්තානයේ සිට 15 km දුරින් ගං ඉවුරේ පිහිටි බලවේග මධ්‍යස්තානයකට යාමට ඔහුට අවශ්‍යව ඇත. ඔහුට  බෝට්ටුව පැදීම 2 kmh^-1 වේගයකින්ද ගං ඉවුර දිගේ පා ගමනින් යාම 4 kmh^-1 වේගයකින්ද කළ හැකි නම්  බලවේග මධ්‍යස්තානයට හැකි ඉක්මණින් ලඟා වීම පිණිස ඔහු විසින් ඉවුරේ කිනම් ස්තානයකට බෝට්ටුවෙන්    පැමිණිය යුතු වේද?

       වේගය = දුර/කාලය

කාලය = දුර/වේගය

මුලු ගමනට ගත වන කාලය T නම්,

         T = \frac{\sqrt{\left(3^2+x^2\right)}}2+\frac{\sqrt{\left(15^2-3^2\right)}{\displaystyle-}{\displaystyle x}}4

         T = \frac{\left(2\sqrt{\left(3^2+x^2\right)}+\sqrt{\left(15^2-3^2\right)}-x\right)}4

T, x විශයෙන් අවකලනය ,

\begin{array}{rcl}&&\frac{dT}{dx}\end{array}= \frac12\left(\frac{\displaystyle(2x)}{2\sqrt{\left(9+x^2\right)}}\;\right)+\frac{\left(0-1\right)}4

             \begin{array}{rcl}&&\frac{dT}{dx}\end{array} = \frac{\displaystyle\sqrt{\left(9+x^2\right)}(2x)}4\;+\frac{\left(0-1\right)}4

             \begin{array}{rcl}&&\frac{dT}{dx}\end{array} =\frac14\left(\frac{\displaystyle(2x)}{\sqrt{\left(9+x^2\right)}}\;-1\right)

ස්තාවර ලක්ෂ්‍ය සඳහා,

\begin{array}{rcl}&&\frac{dT}{dx}\end{array}= 0

\frac14\left(\frac{\displaystyle(2x)}{\sqrt{\left(9+x^2\right)}}\;-1\right) = 0

2x = 2x=\sqrt{9+x^2}

4x² = 9+x²

x ²  =  3

  x = ±√3

x  > 0 නිසා  x = √3

බෝට්ටුව ගං ඉවුරට ඇඳි ලම්භයේ අඩියේ සිට √3 km ක දුරකදී ගං ඉවුරට ලඟා විය යුතුයි.

උදා: (24.)    අරය r වන ගෝලයක් තුළ සෘජු වෘත්ත කේතුවක් අන්තර්ගත කරනු ලැබේ. ගෝලයේ කේන්ද්‍රයේ,        කේතුවේ පතුල ම්ඟින් ආපාතිත අඩ සිරස් කෝණය 2θ නම් කේතුවේ පරිමාව V = V₀[sin²2θ(1+cos2θ)/4] බව පෙන්වන්න. මෙහි V₀ යනු ගෝලයේ පරිමාවයි. ඒ නයින් කේතුවේ පරිමාව උපරිමයක් නම් එය ගෝලයේ පරිමාවෙන් 8/27 ක් බව පෙන්වන්න. 

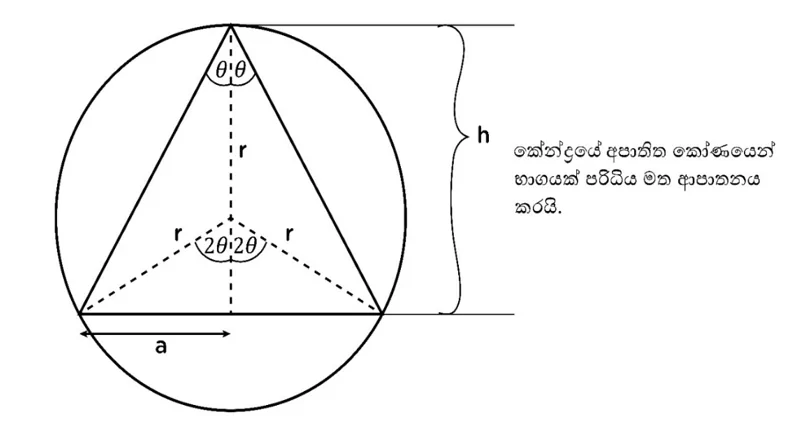
            V = 1/3πa²h

             V = 1/3π (r²sin²2θ) (r+rcos2θ)

             V= (4/3πr³) {sin²2θ (1+cos2θ)/4}

           V = V₀ [sin² 2θ(1+cos2θ)/4]

  \begin{array}{rcl}&&\frac{dv}{d\theta}\end{array}= (V₀/4) {(sin²2θ )(-sin2θ)(2) + (1+cos2θ)(2sin2θcos2θ)(2)}

                \begin{array}{rcl}&&\frac{dv}{d\theta}\end{array} = \frac{v_o}4{-2sin³2θ + 4(1+cos2θ) (sin2θcos2θ)}

                 \begin{array}{rcl}&&\frac{dv}{d\theta}\end{array}= \frac{v_o}2{2(1+cos2θ) (sin2θcos2θ) –sin³2θ}

\begin{array}{rcl}&&\frac{dv}{d\theta}\end{array}= 0

\frac{v_o}2{2(1+cos2θ) (sin2θcos2θ) – sin³2θ} = 0

2(1+cos2θ) (sin2θcos2θ) = sin³2θ

                2cos2θ+2cos²2θ = sin²2θ

                2cos2θ+2cos²2θ = 1-cos²2θ

             3cos²2θ+2cos2θ-1 = 0

       (3cos2θ-1)(cos2θ+1) = 0

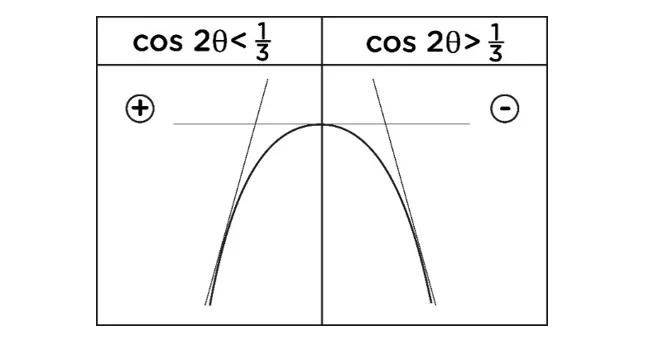
        cos2θ = 1/3      cos2θ = -1   (θ<0 නිසා මෙය ගත නොහැක.)

        cos2θ = 1/3

V max = V₀/4{(1-cos²2θ) (1+cos2θ)}

        V max = V₀/4{(1- 1/9) (1+ 1/3)}

        V max = V₀/4(8/9) (4/3)

        V max = V₀ (8/27)

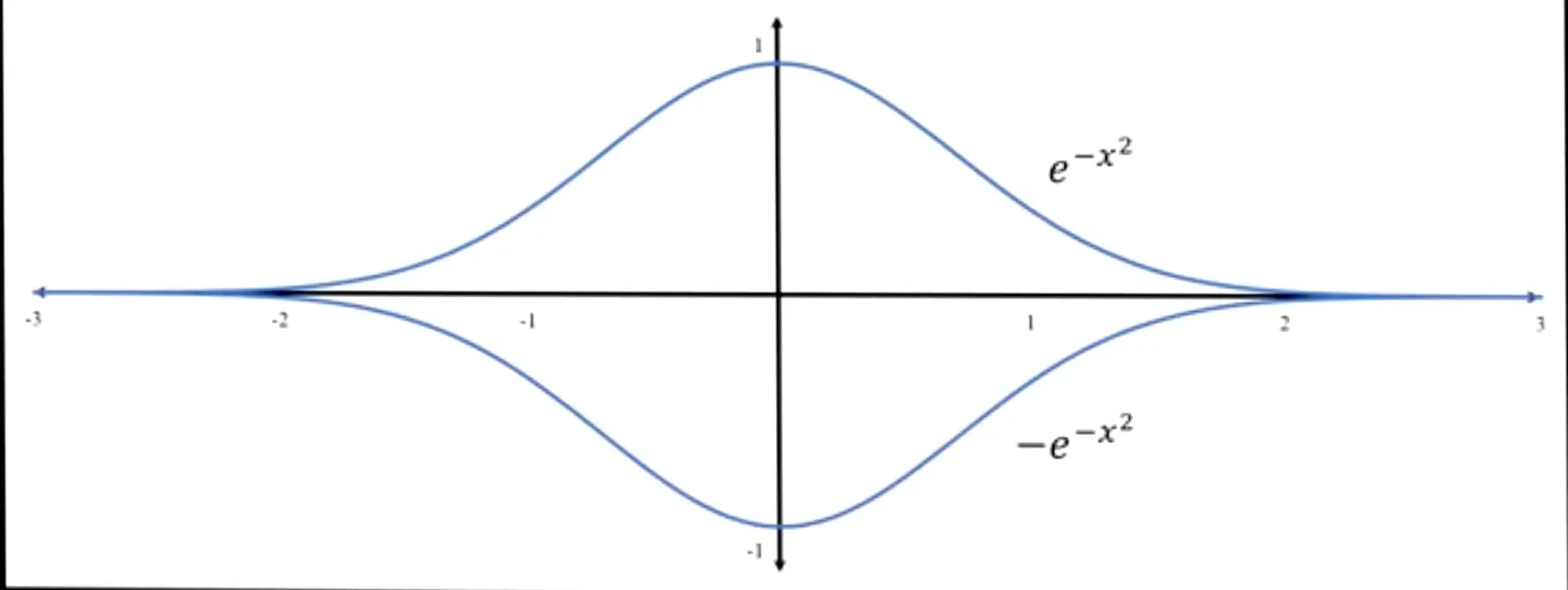
කේන්ද්‍රය (0,0) වන y=e^{-x^2}\;හා\;y=-e^{-x^2} වක්‍රයන් අතර පිහිටන විශාලම වෘත්තයේ වර්ගඵලය සොයන්න.

පිළිතුර පෙන්වන්න

උදා: (25.)    රූපයේ දැක්වෙන්නේ අර්ධ වෘත්තාකාර හා එහි විෂ්‍කම්භය පාදයක් වූ සෘජුකෝණාස්‍රයකින් සං‍යුක්ත වූ රූප සටහනකි. මෙහි පරිමිතිය 20m වේ. මෙහි වර්ගඵලය උපරිම වීමට සෘජුකෝණාස්‍රයට ගත හැකි දිග හා පළල පිළිවෙලින් yහා x නම්, x = 40/(π+4) , y = 20/(π+4) බව පෙන්වන්න.

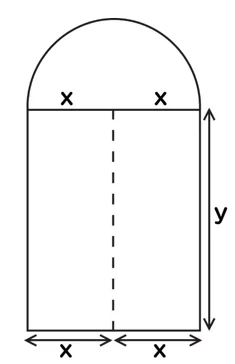
    පරිමිතිය = 2y+2x+ 2πx/2

           20 = 2y+2x+π x

           2y = 20- x (2+π)

වර්ගඵලය A = 2xy+ πx²/2

                    A= x {20-x (2+π)} + πx²/2

                    A = 20x-(2+π). X²+ πx²/2

\begin{array}{rcl}&&\frac{dA}{dx}\end{array}= 20-2x (2+π) + π x

\begin{array}{rcl}&&\frac{dA}{dx}\end{array}= 20-4x-πx

\begin{array}{rcl}&&\frac{dA}{dx}\end{array}= 0

20-4x-πx = 0

         20 = x (4+π)

x = 20/ (4 +π)

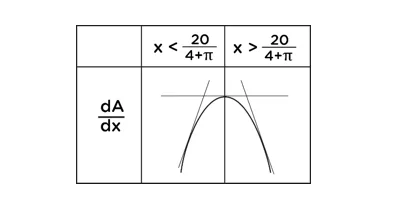
          2x = 40/ (4+π)

2y (4+π) = 20(4+π)-(π+2)20

2y (4+π) = 80+20π-20π-40

           y = 20/ (4+π)

අවකලනය ඇසුරින් ශීඝ්‍රතාවය ලබාගැනීම

• x ට සාපේක්ෂව y වෙනස් වීමේ ශීඝ්‍රතාවය  \begin{array}{rcl}&&\frac{dy}{dx}\end{array} ලෙස අර්ත දැක්වේ.
• s විස්තාපනයක්ද t කාලයක්ද විට,

\begin{array}{rcl}&&\frac{ds}{dt}\end{array}= v (ප්‍රවේගය) = ṡ

\begin{array}{rcl}&&\frac{dv}{dt}\end{array}= a (ත්වරණය) =v

උදා:(26.)  තිරස් රේඛාවක චලනය වන වස්තුවක t කාලයකදී ගමන් කළ දුර s නම්, s=t³-9t²+24t  සමීකරණයෙන් දෙනු ලැබේ.

i.වස්තුවෙහි ආරම්භක ප්‍රවේගය සොයන්න.

ii. s  වැඩිවෙමින් හා අඩුවෙමින් පවත්නා වූ අවස්තා සොයන්න.

i.s=t³-9t²+24t

\begin{array}{rcl}&&\frac{ds}{dt}\end{array}= 3t²-18t+24 = v

a=\begin{array}{rcl}&&\frac{dv}{dt}\end{array}

           a =6t-18

          t=0 විට,

          v=3(0)-18(0) +24

          v=24 ms^-1

• යම් ශ්‍රිතයක් වැඩිවෙමින් පවතින විට \begin{array}{rcl}&&\frac{dy}{dx}\end{array}> 0 වේ.

        යම් ශ්‍රිතයක් අඩුවෙමින් පවතින විට   \begin{array}{rcl}&&\frac{dy}{dx}\end{array}< 0 වේ.

       \begin{array}{rcl}&&\frac{ds}{dt}\end{array}= 3(t2-6t+8)

        \begin{array}{rcl}&&\frac{ds}{dt}\end{array}= 3(t-4) (t-2)

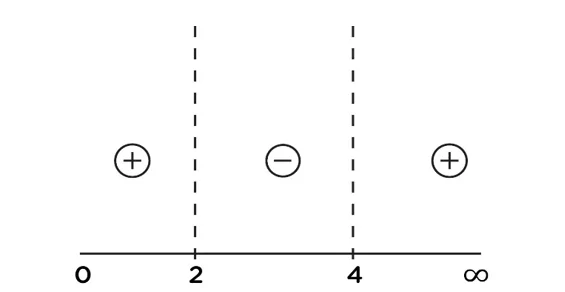
 s වැඩිවෙමින් පවතින විට,    \begin{array}{rcl}&&\frac{ds}{dt}\end{array}> 0

                  0 < x < 2

                  4 < x < ∞

 s අඩුවෙමින් පවතින විට,      \begin{array}{rcl}&&\frac{ds}{dt}\end{array} < 0

                  2 < x < 4

උදා: (27.)    ගෝලයක වර්ගඵලය 4π cm²s^-1 කින් වැඩි වේ. r = 2 cm වන විට,

1. එහි අරය වැඩිවීමේ ශීඝ්‍රතාවය
2. පරිමාව වැඩිවීමේ ශීඝ්‍රතාවය සොයන්න.

1. A = 4πr²

        දෙපසම t විෂයෙන් අවකලනයෙන්,

\begin{array}{rcl}&&\frac{dA}{dt}\end{array}= (4π) (2r) \begin{array}{rcl}&&\left(\frac{dr}{dt}\right)\end{array}

       4π = (4π) (2r) \begin{array}{rcl}&&\left(\frac{dr}{dt}\right)\end{array}

 \begin{array}{rcl}&&\left(\frac{dr}{dt}\right)\end{array}= 1/2r

r = 2 විට,   \begin{array}{rcl}&&\left(\frac{dr}{dt}\right)\end{array}= (1/4) cms^-1

1.  V = (4/3)πr³

               \begin{array}{rcl}&&\left(\frac{dv}{dt}\right)\end{array}= (4/3) (π) (3r²)\begin{array}{rcl}&&\left(\frac{dr}{dt}\right)\end{array}

\begin{array}{rcl}&&\left(\frac{dv}{dt}\right)\end{array}=(4/3) (3πr²)(1/2r)

            \begin{array}{rcl}&&\left(\frac{dv}{dt}\right)\end{array}= 2πr   

r = 2 විට, \begin{array}{rcl}&&\left(\frac{dv}{dt}\right)\end{array}= 4π cm³s^-1

“He who sees things grow from the beginning will have the best view of them.”
– Aristotle –

• වැඩිදුර  විස්තරසඳහා,