සංයුක්ත ගණිතය I (ශුද්ධ ගණිතය) ප්රශ්න පත්රයේ A කොටසේ ගැටලුවක හා B කොටසේ 14 වැනි ගැටලුවෙහි අඩංගු වන්නේ මෙම පාඩමෙහි අඩංගු සිද්ධාන්ත වේ.

කලනය සඳහා භාවිතා වන ඉංග්රීසි නාමය වන “Calculus” යන්න ලතින් බසින් නිර්මාණය වූ වචනයක්.එහි අරුත “කුඩා ගල් කැට” යන්නයි.පෞරාණික රෝමයේ එවැනි කුඩා ගල් කැට වෙළඳුන් විසින් භාණ්ඩ ප්රවාහනයේදී ගමන් කරන දුර මැන ගැනීමට භාවිතා කර තිබෙනවා.මෙම වචනය කලක් තිස්සේ පරිනාමය වීමෙන් පසු අද වන විට ‘ගණන් කිරීමේ ක්රමයක්’ යන අරුත ලබා දෙනවා. ∴මෙම ලතින් නම කලනය යන විශේෂ ගණිත ක්රමය හැඳින්වීමට භාවිතා කර තිබෙනවා.17 වන සියවසේදී යුරෝපයේ විසූ Isaac Newton හා Gottfried Wilhelm Leibniz යන ගණිතඥයන් දෙදෙනා දාම නීතිය, ගුණන නීතිය වැනි කරුණු ඉදිරිපත් කරමින්, කලනය යන ගණිත සංකල්පය තවදුරටත් පුළුල් කිරීමට දායක වී තිබෙනවා. මෙම පාඩමේදී අපි ඉගෙන ගන්න යන්නේ කලනය යන මාතෘකාව යටතේ එන අවකලනය පිළිබඳවයි.
වෘද්ධිය
- විචල්ය රාශියක ඇති වන ඉතා කුඩා වෙනසක් වෘද්ධියක් ලෙස හදුන්වයි. කලනය කොටසේදී මෙය ඩෙල්ටා(\Delta )ලෙස අංකනය කරයි.
උදාහරණ: x හි ඇතිවන කුඩා වෙනසක් ∆x වේ.
වෘද්ධි අනුපාතය
- y යනු x හි ශ්රිතයක් විට x ට ∆x වෘද්ධියක් ලබා දුන් විට y හි ඇතිවන වෘද්ධිය ∆y වේනම්, \frac{\triangle y}{\triangle x} ට වෘද්ධි අනුපාතය යැයි කියනු ලැබේ.
අවකලන සංගුණකය අර්ථ දැක්වීම
- y යනු x හි ශ්රිතයක් විට x ට වෘද්ධියක් ලබා දුන් විට y හි ඇතිවන වෘද්ධිය ∆y නම්
lim ∆x→0 \frac{\triangle y}{\triangle x} , x විශයෙන් y හි ප්රථම ව්යුත්පන්නය හෙවත් අවකලන සංගුණකයයි.
මෙය \frac{\operatorname dy}{\operatorname dx} ලෙස කලනයේදී අංකනය කරයි.
එනම්, lim ∆x→0 \frac{\triangle y}{\triangle x}=\frac{\operatorname dy}{\operatorname dx}
අවකලන සංගුණකය අර්ථ දැක්වීම තවත් ආකරයකින්
- f යනු x හි ශ්රිතයක් විට x ට ∆x වෘද්ධියක් ලබා දුන් විට f(x) හි ඇතිවන වෘද්ධිය \;f(x+\bigtriangleup x)–f(x) නම්,
x විශයෙන් f(x) හි පළමු ව්යුත්පන්නය හෙවත් පළමු අවකලන සංගුණකය නම් වේ.
එනම්, \;\;\;\lim_{\triangle x\rightarrow0}\frac{f(x+\triangle x\;)\;–\;f(x)}{\triangle x}\;\;=f'\left(x\right)
y යනු x හි ශ්රිතයක් විට,
y = f(x) →\boxed1
x ට ∆x වෘද්ධියක් ලබා දුන් විට y හි වෘද්ධිය ∆y වේ නම්,
y +∆y = f(x+∆x) →\boxed2
\boxed2 - \boxed1 න්,
\triangle y=\;f\left(x+\triangle x\right)-f(\triangle x)
\frac{\triangle y}{\triangle x}=\;\frac{f\left(x+\triangle x\right)-f(\triangle x)}{\triangle x}
\lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x}=\;\lim_{\triangle x\rightarrow0}\frac{f\left(x+\triangle x\right)-f(\triangle x)}{\triangle x}
\frac{dy}{dx}=\text{f}^/\left(x\right)
ශ්රිතයක අවකලන සංගුණකය සෙවීම
- ශ්රිතයක අවකලන සංගුණකය සෙවීම අකර දෙකකි.
1.මූලික මූලධර්ම ඇසුරින්
2.සූත්ර මඟින්
මූලික මූලධර්ම මඟින්
- y=x2 ප්රථම මූලධර්ම ඇසුරින් අවකලනය කරන්න.
y = x2 → \boxed1
x ට ∆x වෘද්ධියක් ලබා දුන් විට y හි වෘද්ධිය ∆y නම්
y +∆y = (x+∆x)2 → \boxed2
\boxed2 - \boxed1 න්,
\frac{\triangle y}{\triangle x}=\frac{\displaystyle(x+\triangle x)^2\;‒x^2}{\triangle x}\lim_{\triangle x\rightarrow0}\;\;\frac{\;\triangle y\;}{\triangle x}\;=\;\lim_{\triangle x\rightarrow0}\;\;\;(\frac{\;x^2\;+\;2x\triangle x\;+\;\triangle x^2\;–\;x^2\;)}{\triangle x}
\frac{dy}{dx} = 2x
- y =√x ප්රමූලධර්ම මඟින් අවකලනය කරන්න.
y = √x →\boxed1
x ට ∆x වෘද්ධියක් ලබා දුන් විට y හි වෘද්ධිය ∆y වේ නම්,
y +∆y =√ (x+∆x) → \boxed2
\boxed2 - \boxed1 න්,
\frac{\;\triangle y}{\triangle x}\;\;=\;\frac{\surd\;(x+\triangle x)\;‒\;\surd x}{\triangle x}\;\lim_{\;\triangle x\rightarrow0}\;\;\;\frac{\triangle y}{\triangle x}\;\;=\;\lim_{\;\triangle x\rightarrow0}\;\frac{(\;\surd\;(x+\triangle x)\;‒\;\surd x)(\surd\;(x+\triangle x)\;+\;\surd x\;}{\;\triangle x(\surd\;(x+\triangle x)\;+\;\surd x\;)})\;
\frac{\;dy}{dx}\;\;\;=\lim_{\;\triangle x\rightarrow0}\;\;\;\;\;\frac{(x\;+\;\triangle x\;–\;x\;)}{\triangle x(\surd\;(x+\triangle x)\;+\;\surd x\;)}\;
\frac{dy}{dx}=\frac1{\sqrt2}
- y = [ f(x)]2 ප්රමූලධර්ම මඟින් අවකලනය කරන්න.
y = [ f(x)]2 → \boxed1
x ට ∆x වෘද්ධියක් ලබා දුන් විට y හි වෘද්ධිය ∆y වේ නම්,
y +∆y =[f (x+∆x)]2 → \boxed2
\boxed2 - \boxed1 න්,
\frac{\triangle y}{\triangle x}\;\;=\frac{\;\lbrack f\;(x+\triangle x)\rbrack^2\;‒\;\lbrack\;f(x)\rbrack^2}{\triangle x}\lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x}\;\;=\lim_{\triangle x\rightarrow0}\frac{\;\lbrack f\;(x+\triangle x)\rbrack^2\;‒\;\lbrack\;f(x)\rbrack^2}{\triangle x}
\frac{dy}{dx}\;=\lim_{\triangle x\rightarrow0}\frac{\lbrack\;f\;(x+\triangle x)\;‒\;\;f(x)\rbrack\lbrack\;f\;(x+\triangle x)\;+\;f(x)\rbrack\;\;}{\triangle x}
\frac{dy}{dx}\; = \frac{lim\;\triangle x\rightarrow0\;\lbrack f\;(x+\triangle x)\;‒\;f(x)\rbrack\;.\;lim\;\triangle x\rightarrow0\;\lbrack f\;(x+\triangle x)\;+\;f(x)\rbrack\;}{\triangle x}
\frac{dy}{dx}\; = f /(x) 2f(x)
සූත්ර මඟින් අවකලනය
1. නියතයක අවකලන සංගුණකය සෙවීම.
c යනු නියතයක් විට,
y = c , \frac{dy}{dx} = 0 වේ. c ; නියතයකි.
2. xn අවකලනය සඳහා සූත්රය.
y= xn → \boxed1
x ට ∆x වෘද්ධියක් දුන් විට y හි වෘද්ධිය ∆y නම්,
y +∆y =(x+∆x)n → \boxed2
\boxed2 - \boxed1 න්,
∆y = (x+∆x)n ‒ (x)n
\frac{\triangle y}{\triangle x}\;\;=\;\;\frac{(x+\triangle x)^n\;‒\;\;(x)^n}{\triangle x} \lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x}\;\;=\;\lim_{\triangle x\rightarrow0}\;\frac{(x+\triangle x)^n\;‒\;\;(x)^n}{(x+\triangle x)-x}\frac{dy}{dx} = nxn-1
y= xn ; \frac{dy}{dx} = nxn-1 (n= පරිමේය සංඛ්යාවකි)
3. y = x5
\frac{dy}{dx} = 5x4
4. y = √x
\frac{dy}{dx} = \frac1{2\sqrt x}
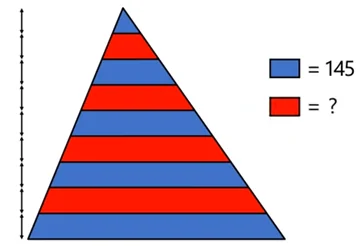
රූපයේ පරිදි ත්රිකෝණයක් සමාන තීරුවලට බෙදා එකක් හැර එකක් රතු හා නිල් වර්ණවලින් වර්ණ ගන්වා තිබේ.නිල් පැහැයෙන් වර්ණ ගන්වන ලද තීරුවල මුළු වර්ගඵලය 145ක් වේ. රතු පැහැයෙන් වර්ණ ගන්වන ලද තීරුවල මුළු වර්ගඵලය කීයද?
ශ්රිතයක් නියතයකින් ගුණ වී ඇති විට අවකලන සංගුණකය
- f යනු x හි ශ්රිතයක්ද c නියතයක්ද විට, y = cf(x)
y = c f(x) → \boxed1
x ට x වෘද්ධියක් දුන් විට y හි වෘද්ධිය ∆y නම්,
y +∆y = c f (x+∆x) → \boxed2
\boxed2 - \boxed1 න්,
∆y = c [ f (x+∆x) ‒ f(x)]
\frac{\;\triangle y}{\;\;\triangle x\;}\;\;=\frac{c\;\lbrack\;f\;(x+\triangle x)\;‒\;f(x)\rbrack}{\;\;\triangle x}\lim_{\triangle x\rightarrow0}\frac{\;\triangle y}{\;\;\triangle x\;}\;\;=\lim_{\triangle x\rightarrow0}\frac{c\;\lbrack\;f\;(x+\triangle x)\;‒\;f(x)\rbrack}{\;\;\triangle x}
\frac{\operatorname dy}{\operatorname dx} = c f /(x)
- y = 3x4
\frac{dy}{dx} = 12x3
ශ්රිත දෙකක එකතුවෙහි අවකලනය
- u හා v යනු x හි අවකල්ය ශ්රිත විට,
y = u + v →\boxed1
x ට ∆x වෘද්ධියක් දුන් විට u හි වෘද්ධිය ∆u ද v හි වෘද්ධිය ∆v ද y හි වෘද්ධිය ∆y ද නම්,
y + ∆y = ( u+∆u) + (v+ ∆v) → \boxed2
\boxed2 - \boxed1 න්,
∆y = ( u+∆u) + (v+ ∆v) – u ‒ v
\frac{\triangle y}{\;\triangle x\;\;}\;\;=\;\frac{\;(\;u+\triangle u)\;+\;(v+\;\triangle v)\;–\;u\;‒\;v}{\;\triangle x\;\;} \;\;\;\lim_{\triangle x\rightarrow0}\;\;\frac{\;\triangle y}{\triangle x}\;\;=\lim_{\triangle x\rightarrow0}\;\;\;\frac{\triangle u}{\triangle x}\;\;+\;\lim_{\triangle x\rightarrow0}\;\;\frac{\triangle v}{\triangle x}\;\frac{dy}{dx}\;\;\;=\;\frac{\;du\;\;}{dx}+\;\;\frac{\;dv}{dx}
- y = 3x2 + 5x
\;\frac{dy}{dx}\;\;\; = 6x + 5
ශ්රිත දෙකක අන්තරය සඳහා සූත්රය
- u හා v යනු x හි අවකල්ය ශ්රිත විට,
y = u ‒ v → \boxed1
x ට ∆x වෘද්ධියක් දුන් විට u හි වෘද්ධිය ∆u ද v හි වෘද්ධිය ∆v ද y හි වෘද්ධිය ∆y ද නම්,
y + ∆y = ( u+∆u) ‒ (v+ ∆v) → \boxed2
\boxed2 - \boxed1 න්,
\;\;\;\;\frac{\triangle y}{\;\triangle x\;\;}\;\;=\;\;\frac{(\;u+\triangle u)\;‒\;(v+\;\triangle v)\;–\;u\;+\;v}{\;\triangle x\;\;}\lim_{\triangle x\rightarrow0}\frac{\;\triangle y\;}{\triangle x}\;=\lim_{\triangle x\rightarrow0}\;\;\frac{\triangle u}{\triangle x}\;\;‒\lim_{\triangle x\rightarrow0}\;\;\frac{\triangle v}{\triangle x}
\;\;\frac{\;\;\;\;dy\;}{dx}\;\;=\;\frac{\;du}{dx}\;\;‒\;\;\frac{\;dv}{dx}
- y = x3 ‒ 2√x + 1/√x
\frac{dy}{dx}\;\;\;\;=\frac{\;3x^{2\;}}{}–\frac{\;1}{\surd x}\;–\;\;\;\frac{\;1}{\;2x^{3/2}\;\;\;}
ශ්රිත දෙකක ගුණිතයෙහි අවකලනය සඳහා සූත්රය
- u හා v යනු x හි අවකල්ය ශ්රිත විට,
y = u v → \boxed1
x ට ∆x වෘද්ධියක් දුන් විට u හි වෘද්ධිය ∆u ද v හි වෘද්ධිය ∆v ද y හි වෘද්ධිය ∆y ද නම්,
y + ∆y = ( u+∆u) (v+ ∆v) → \boxed2
\boxed2 - \boxed1 න්,
- \lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow0}\frac{(vu+\triangle vu+v\triangle u+\triangle v\triangle u)-vu}{\triangle x}
- \lim_{\;\triangle x\rightarrow0}\;\frac{\triangle y}{\;\triangle x}\;\;=\;\;\lim_{\;\triangle x\rightarrow0}\;\frac{\;u\triangle v\;\;+\;v\triangle u\;+\;\triangle u\triangle v}{\triangle x}
- \frac{\operatorname dy}{\operatorname dx}\;\;=\;u\lim_{\;\triangle x\rightarrow0}\;\frac{\triangle v}{\triangle x}\;\;\;+\;\;\;v\lim_{\;\triangle x\rightarrow0}\;\frac{\triangle u}{\triangle x}+\;\frac{\lim_{\;\triangle x\rightarrow0}\;\;\triangle u\;\;\;\lim_{\;\triangle x\rightarrow0}\;\;\triangle v\;\;}{\triangle x}
- \;\frac{\;dy}{dx}\;\;\;=\;u\frac{\;du}{dx}\;\;+\;\;v\frac{\;dv}{dx}\;\;+\;0
උදාහරණ :
1. y = (x2 + 2x – 1 )(x3 + 3)
\frac{\operatorname dy}{\operatorname dx}= (x2 + 2x – 1 )(3x2) + (x3 + 3)(2x + 2 )
= 3x4 + 6x3 – 3x2 + 2x4 + 2x3 + 6x + 6
= 5x4 + 8x3 – 3x2 + 6x + 6
- u හා v යනු x හි අවකල්ය ශ්රිත විට y = uv නම් y හි අවකලන සංගුණක ලබා ගැනීමේ සූත්රය ලියා එනයින් w යනු x හි තවත් ශ්රිතයක් විට,
y = uvw හි \frac{\operatorname dy}{\operatorname dx}=\left(u\frac{\operatorname dv}{\operatorname dx}+v\frac{\operatorname du}{\operatorname dx}\right)w+\left(uv\right)\frac{\operatorname dw}{\operatorname dx} බව අපෝහනය කරන්න
එනයින් y= (x2 + 1)(x + 1)(2x + 3) හි \frac{\operatorname dy}{\operatorname dx} ලබා ගන්න.
y = uv
\frac{\operatorname dy}{\operatorname dx}=u\frac{\operatorname dv}{\operatorname dx}+\frac{\operatorname du}{\operatorname dx}vy = uvw
\frac{\operatorname dy}{\operatorname dx}=\left(u\frac{\operatorname dv}{\operatorname dx}+v\frac{\operatorname du}{\operatorname dx}\right)w+\left(uv\right)\frac{\operatorname dw}{\operatorname dx}2. y= (x2 + 1)(x + 1)(2x + 3)
\frac{\operatorname dy}{\operatorname dx} = (x2 + 1)(x + 1) 2 + (x + 1)(2x + 3) 2x + (x2 + 1)(2x + 3)
=2(x3 + x2 + x + 1) +2x(2x2 + 5x + 3) +(2x3 + 3x2 + 2x+3)
= 8x3 + 15x2 + 10x + 5
ලබ්ධියක අවකලන සංගුණකය ලබා ගැනීම සඳහා සූත්රය
- u හා v යනු x හි අවකල්ය ශ්රිත විට,
y = u / v → \boxed1
x ට ∆x වෘද්ධියක් දුන් විට u හි වෘද්ධිය ∆u ද v හි වෘද්ධිය ∆v ද y හි වෘද්ධිය ∆y ද නම්,
y + ∆y = \frac{\;\;(\;u+\triangle u)}{\;(\mathrm v+\;\triangle\mathrm v)} → \boxed2
\boxed2 - \boxed1[latex] න්,</p> <ul><li> [latex] \frac{\triangle y}{\triangle x}=\frac{\displaystyle\frac{\;\;(\;u+\triangle u)}{\;(\mathrm v+\;\triangle\mathrm v)}-\frac uv}{\triangle x}
- \;\;\lim_{\triangle x\rightarrow0}\;\;\frac{\;\triangle y}{\triangle x}\;\;=\;\;\lim_{\triangle x\rightarrow0}\;\frac{uv\;+\;\;\;v\triangle u\;–\;uv\;\;-\;u\triangle v}{\;v(v+\;\triangle v)\;\triangle x}
- \;\;\frac{dy}{dx}\;\;=\;\;\lim_{\triangle x\rightarrow0}\;\frac{\;\;v\triangle u\;\;-\;u\triangle v}{\;\;\;(v^2+\;v\triangle v)\;\triangle x\;}
- \;\;\frac{dy}{dx}\;\;=\;\;\lim_{\triangle x\rightarrow0}\;v\frac{\triangle u\;}{\;\triangle x\;\;\;\;\;}\;‒\lim_{\triangle x\rightarrow0}\;u\frac{\triangle v}{\;\triangle x\;\;\;\;\;}\;\lim_{\triangle x\rightarrow0}\;\;\frac{\;\;1}{v^2\;+\;v\triangle v\;\;\;\;\;}
- \frac{\;dy}{dx}\;\;\;=\frac{\;v\;{\displaystyle\frac{du}{dx}}\;\;\;‒\;\;\;u\;{\displaystyle\frac{dv}{dx}}\;}{v^2}
y = u/v
\frac{\;dy}{dx}\;\;\;=\frac{\;v\;{\displaystyle\frac{du}{dx}}\;\;\;‒\;\;\;u\;{\displaystyle\frac{dv}{dx}}\;}{v^2}
උදාහරණ :
1. y\;=\;\;\frac{x\;+\;1}{\;x^2\;-\;4}
= \;\;\frac{\;dy\;}{dx}\;=\;\;\frac{\;(\;x^2\;–\;4\;)\;–\;(\;x\;+\;1)\;2x}{\;\;(\;x^2\;–\;4\;)2\;\;}
= \frac{x^{2\;}–\;4\;–2x^2\;–\;2x}{(\;x^2\;–\;4\;)^2\;}
=\frac{-x^2-2x-4}{(x^2-4)}
2. \;y\;=\frac{\;(\;x^2\;+\;3x\;–\;1\;}{\;(x^3\;–\;2x\;+\;1)})
\frac{\;dy}{\;\;dx\;\;}\;\;=\;\;(\frac{x^3\;–\;2x\;+\;1)(2x\;+\;3)\;‒\;(\;x^2\;+\;3x\;–\;1\;)(3x^2\;–\;2)}{(x^3\;–\;2x\;+\;1)^2}
= \;\frac{\;‒\;x^4\;‒\;6x^3\;+\;x^2\;\;+\;2x\;+\;1}{\;(x^3\;–\;2x\;+\;1)^2}
ශ්රිතයක ශ්රිතයක් අවකලනය
- y = (x2 + 5x - 3 )8 සළකමු.
මෙහි u = x2 + 5x - 3 ආදේශය යොදමු.
එවිට u යනු x හි ශ්රිතයකි. එවිට y = u8 වේ. y, u හි ශ්රිතයකි.එමනිසා y = (x2 + 5x - 3 )8 ශ්රිතයක ශ්රිතයක්
වේ.
ශ්රිතයක ශ්රිතයක් අවකලනය සඳහා සූත්රය
- u යනු x හි ශ්රිතයක්ද y යනු u හි ශ්රිතයක්ද යැයි ගනිමු.
x ට ∆x වෘද්ධියක් දුන් විට u හි වෘද්ධිය ∆u ද v හි වෘද්ධිය ∆v ද y හි වෘද්ධිය ∆y ද නම්,
- \frac{\triangle y}{\triangle x}\;\;=\;\;\;\frac{\triangle y}{\triangle u}\;\;\times\;\;\frac{\triangle u}{\triangle x}\;
- \lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x}\;\;=\;\lim_{\triangle x\rightarrow0}\;\;\frac{\triangle y}{\triangle u}\;\;\times\;\;\frac{\triangle u}{\triangle x}\;
- \lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x}\;\;=\;\lim_{\triangle x\rightarrow0}\;\;\frac{\triangle y}{\triangle u}.\;\;\;\lim_{\triangle x\rightarrow0}\;\;\frac{\triangle u}{\triangle x}\;
- \lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x}\;\;=\;\lim_{\triangle u\rightarrow0}\;\;\frac{\triangle y}{\triangle u}.\;\;\;\lim_{\triangle x\rightarrow0}\;\;\frac{\triangle u}{\triangle x}\;
\frac{\operatorname dy}{\operatorname dx}=\frac{\operatorname dy}{\operatorname du}\times\frac{\operatorname du}{\operatorname dy}
- ඉහත ප්රතිඵලය ශ්රිත ඕනෑම ගණනක් පැවැති අවස්ථා සඳහා විස්තීරණය කළ හැක. එබැවින් මෙය දාම නීතිය නම් වේ.
උදාහරණ :
- y = (x2 + 5x - 3)8 අවකලනය කිරීමට දාම නීතිය යොදමු.
x2 + 5x – 3 = u
y = u8
\frac{dy}{du} = 8u7 \frac{du}{dx} = 2x + 5
\frac{\operatorname dy}{\operatorname dx}=\frac{\operatorname dy}{\operatorname du}\times\frac{\operatorname du}{\operatorname dy}
= 8u7 × (2x + 5)
= 8(x2 + 5x – 3)(2x + 5)
2. y =√( x2 + 3x – 1)
u = x2 + 3x – 1
y = √u
\frac{dy}{du}=\frac1{2\sqrt u} \frac{du}{dx}=2x+5
\frac{\operatorname dy}{\operatorname dx}=\frac{\operatorname dy}{\operatorname du}\times\frac{\operatorname du}{\operatorname dy}
= \frac1{2\sqrt u}.\left(2x+3\right)
= \frac{\left(2x+3\right)}{2\sqrt{\left(x^2+3x-1\right)}}
3.y = ( x3 – 5x + 1)10
\frac{dy}{dx} = 10(x3 – 5x + 1)9 (3x2 - 5)
“Infinity converts the possible into the inevitable.”
-Norman Cousins-

